Trapezoid Bolt

Simplification in progress ...

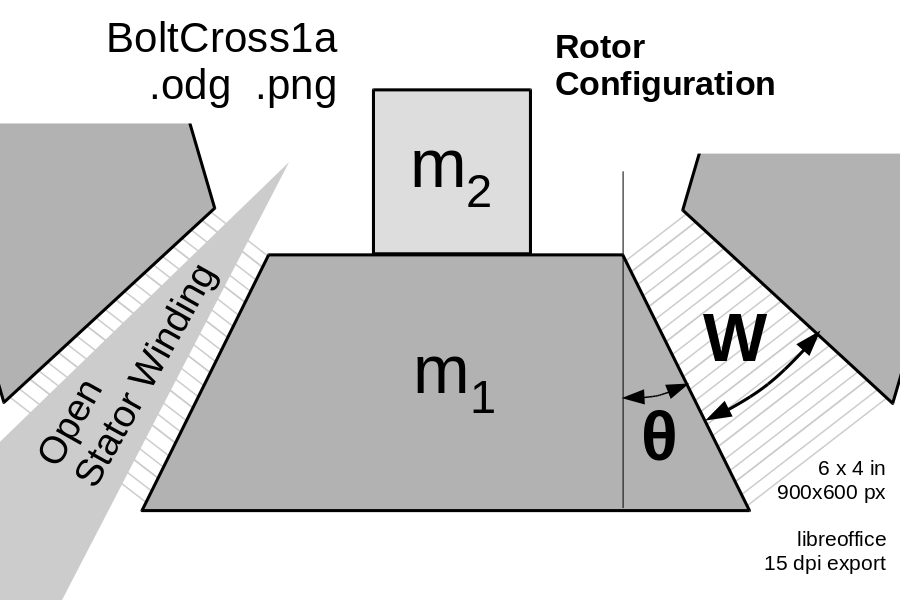
The launch loop rotor is composed of separable bolts, mostly made of thin laminations of transformer steel, along with carbon fiber stiffeners, embedded aluminum induction motor conductors, and a central spine. The bolts are normally used in two modes; assembled into a multilobed rotor for the main tracks and inclines, and separated into separate bolts for minimum radius deflection.

The number of lobes in the rotor (and the number of bolts in parallel) remains to be determined; probably 4 or 6. The length of the bolts also will be determined later; gaps between lengths will change with velocity, and the gaps will interrupt the motor field and cause some vibration in the vehicle sked. The size and cross section of the rotor is constrained by its linear density; the current estimate is 43.2 grams per centimeter of rotor length, or 4.32 kg per meter.

Rotor Mode

The angle of the faces can be computed from the geometry of the assembled rotor, and the stator wedge shape of the stator windings and the wedge-shaped stator winding gaps penetrating it. (Note 1) If there are N lobes, and the stator wedges have an angle of W degrees, then the angle of both faces of the trapezoidal bolt are 360/N-W, and the angle on each face is half that, θ = 180/N - W/2. Here's some plausible bolt face angles:

The stator wedge angle may be zero; it will probably be small. The "wedge" will be a layer of thin radial windings to a busbar in the middle. The windings will be wrapped in carbon fiber for stiffness; the resonant modes should be much higher frequency than the fastest bolt passage frequency, and there should be some means to rapidly damp the vibrations; a thicker and stiffer root at the outer end of the wedge will enable this. the wedge (and all other vacuum-facing surfaces) will be coated with durable tool diamond, and very smooth, though ridges may be added to pump stray gas molecules towards the edge.

The stator wedge will be excited very briefly - if the sled is 50 meters long, and the sled is moving 10.5 km/s relative to the 12.5 km/s rotor, then the windings will only be excited for 25 milliseconds. Assume the generator process is 95% efficient. A 6000 kg, 30 m/s² launch is 180 KN, and 1.89 GW. If the generator process is 95% efficient, it may deposit 95 MW into the windings as they zip through the sled zone: 1.9 MW per meter, or 48 KJ/meter over 25 milliseconds. If the windings are copper, with an average specific heat of 375 J/kg/K and mass 0.5 kg/m, the windings will impulse heat with a delta of 260K; the heating rate will be 10,000 C per second. Ambient temperature at 80 km altitude is 190K; if the wedges couple to that with a heat sink with 200K thermal difference, the copper may heat (briefly) to 650K, less than 400C . The wedges must not deform, deflect or embrittle with repeated heat shocks like this, perhaps as often as 10 million shocks per decade.

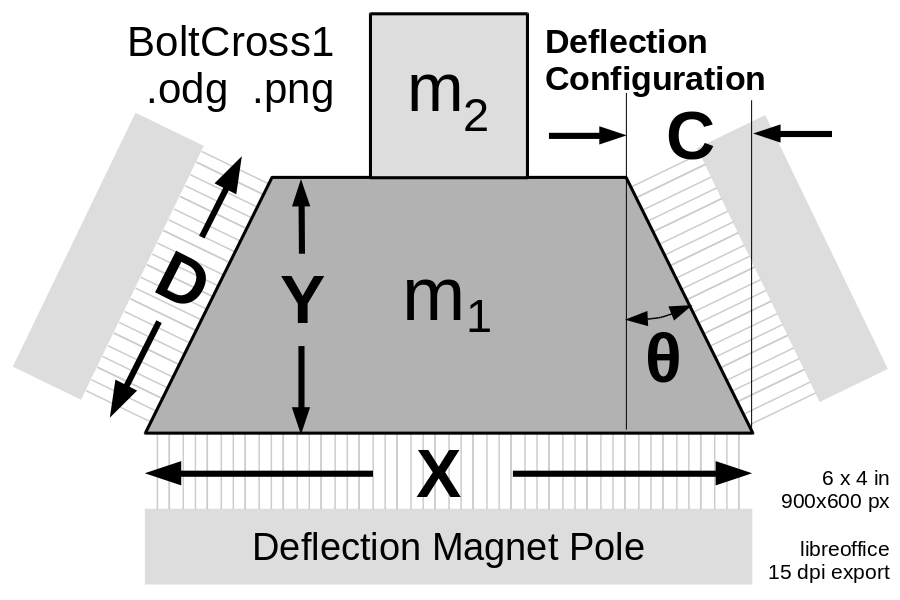
Deflection Mode

The radius of the ambit and upturn deflection magnets are constrained by acceleration, rotor mass density, and maximum deflection force. An electromagnet pole (shown at the bottom of this diagram) pulls the rotor towards it, with near-saturation flux density B_{max} , perhaps 1.8 Tesla. The material will be strongly saturated and with considerable hysteresis at this field strength; hysteresis helps regulate the deflection force, though it increases the controller power necessary to modify it.

For a 4.32 kg/m rotor with six bolts arranged in a hexagon, each bolt will mass 7.2 grams per centimeter of length. If 30% of the bolt mass is non-iron mass m₂, and 70% of the bolt is m₁, then m₁ is approximately 5 g/cm = 5e-3 kg/m.

The density of 4% silicon transformer steel is 7.65 g/cm³, so A₁, the cross section of the area with mass m₁, is A₁ = 0.65 cm² = 6.5e-5 m².

We can use a trick to maximize the field strength at the bottom; we can direct flux vertically from below, and almost horizontally from the faces on the sides. There will be some vertical flux component from the sideways forces, but if θ is small, the vertical force "loss" will be small as well.

The (attracting) deflection force at the bottom is F_X ~=~ X ~×~ B_{max}^2 / 2 \mu_0 so F_X = X × 1.29 MPa . The force at each diagonal face is half that. The fraction of the force directed upwards is F_X \sin( 0 ), twice the upwards force at each side face. So, the total downwards deflection force is:

For a six lobe rotor with a 10 degree stator wedge, and a bolt area of 0.65 cm², the bolt dimensions are:

The stator-to-rotor gap has an enormous velocity difference of 12.5 km/s; the vacuum must be very good and the faces strong, mirror-smooth, and tool-diamond-coated, for minimal sputter yield. The plenums radially beyond the bolts will be constructed with turbine blades (also diamond-coated) deflecting residual gas atoms outwards and away from the rotor, to more pumps outside the primary track containment. The vacuum does not need to be as good as a particle accelerator such as the Large Hadron Collider, but it should be good enough to minimize erosion, hopefully keeping the rotor and walls intact for years. The details of the design will evolve from years of experience with smaller, slower Power Storage Loops.

Assume a stator width of 3 mm at the outer edge of the bolt, and a stator-to-rotor gap of 3 mm, for an outer gap width of 9 mm and an inner gap width of The resulting six lobe rotor will be bounded by a hexagon with a face length of 23.88 mm. The face-to-face dimension will be 41.36 mm, and the outer gap-to-gap dimension will be 37.36 mm. The distance between the rotor trapezoids will be 9 mm at the outside and 7.825 mm at the inside; this will concentrate the circumferential rotor flux towards the center. We can expect the flux to expand radially from the gap, roughly 4.5 mm to the outside and 3.9 mm towards the inside, so the radial windings of the stator wedge should extend from 8 mm to 20 mm radially from the rotor centerline.

MoreLater

Note 1: The spacing between hyperspeed rotor and the wire stator must be maintained actively by globally aware electronics. If the stator contacts the rotor in any channel anywhere along the 6000 km length of the rotor, the rotor and stator will be vaporized and the entire launch loop will fail. This is almost impossible, and will only become possible after years of development and high volume deployment of lower speed power storage loops. Technology evolves, and intermediate evolutionary steps and accumulated experience is required. Spacing control will require redundant electronics, and some means of rapidly withdrawing short sections of stator outwards from the bolt stream if any anomalies are detected.