PowerLoop
Note: The following is being rewritten more coherently. This website is a work in progress. Your patience is appreciated!
|
A simplified version of Launch Loop technology can be used to store global-scale energy. Peak load power production and transmission on an international scale will pay for the development and optimization of loop technology, while financing the expansion of life into the solar system. A shared global power storage system will move power around the Atlantic and Pacific oceans, moving unused power around the world to peak loads in eastern Asia, North America, and Europe. Later, power loops will connect South America with Australia and Africa, and Africa with India and Australia. |
Buckminster Fuller pointed out that a globally shared power grid is a powerful incentive for peace. If 50% of your country's peak load energy comes from other countries, it is stupid to attack them, immediately crippling your domestic economy. Nations are capable of great stupidity, and war is one of the stupidest things they do, so a global power economy will not ensure world peace. But it can help make citizens wealthy and cosmopolitan enough to resist the calls of the demagogues. Here's hoping!
Hundreds or thousands of power loops may be constructed on paths along the lower continental shelf, with emergency rotor dump zones sited in lifeless portions of the deep ocean. Prudent "design for failure" will minimize risk to human and animal life. Indeed, a dumped rotor may stir up bottom sediments, providing nutrients for plankton, attracting fish and fishermen to these dump sites, subjecting them to the risk of future rotor dumps. Paradoxically, increasing the abundance of life can lead to more death. But increasing experience and improved designs will reduce these expensive accidents over time.
Eventually, when rotor and magnetic deflection technology matures, and hyper-automated production of power loops drives costs to unimaginable lows, power loop technology will evolve into launch loops. Power loops will be the way we move power from mid-oceanic space power receiving antennas, and to mid-oceanic launch loops.
How Power Loops differ from Flywheels
TL-DR summary: The cost of magnetically-deflected loops scale with radius. The stored energy scales as radius squared. Ocean-sized loops can store terawatt-years vastly cheaper than batteries, flywheels, gravity towers, etc.
Flywheel speed is limited by the strength to weight ratio of physical materials. Flywheel energy is stored in moving mass - the mass is confined by centripedal acceleration as it moves around a central hub. Conventional flywheels provide the acceleration either by radial or circumferential structural stress in very strong materials like carbon fiber. Unfortunately, the supporting carbon fiber also has mass, which requires further support.
Radially supported flywheels can be optimized with tapered cross sections - but this makes them difficult to analyze and compare. Circumferentially stressed flywheels are simple, and (take my word for it) follow the same scaling laws, so let's look at the scaling for the simpler form.
Assume a cylindrical rotor with radius R, height H, and thickness T (all in meters). Assume T<<R. It is made from a very strong material such as carbon fiber, with strength S (expressed in Pascals, or Newtons/m2, or Kg/m-s2) and density ρ (expressed in Kg/m3). Assume the rotor is spinning around the axis with velocity V (in m/s).
Consider an element of the rotor between angle θ and θ+dθ. It has a length of R dθ and a mass of ρ T H R dθ and is accelerated radially with an acceleration of V2/R . The radial force on this element is ρ T H V2 dθ .
Imagine slicing the cylindrical rotor in half, and calculate the tensile force F at the two slices. This is the integral of the force perpendicular to the slice - the integral over sin(θ) from 0 to 90 °. So F = ρ T H V2 at each slice. The tensile strength of the slice is F = S T H. So the velocity permitted by the tensile strength is V2 = S / ρ , which is independent of R or T or H. A small flywheel makes more revolutions per second, but the maximum rim speed is the same as a big flywheel. A tapered, center-supported flywheel might go somewhat faster, but the proportionality to strength over mass density is the same.
The space elevator community measures the "characteristic strength" S / ρ in Yuris, named after space elevator inventor Yuri Artsutanov. One Yuri is one meter squared per one second squared. A handy unit. Typical materials are less than a MegaYuri, limiting velocities to less than a kilometer per second. Beacon Power's deployed 25MW flywheels have a rim speed of "1500 mph" or 670 m/s, though they probably can design systems that turn as fast as 1500 m/s with very good materials and advanced design. The nonlinear forces in a high speed rotating frame can distort structural members and create stress concentrations leading to early failure. The same can be caused by voids in bonding materials, causing fibers to "creep" at the ends. Over many speedup/slowdown cycles, stresses can build towards failure. Only with decades of experience, extensive failure analysis, and meticulous quality control will the flywheel companies push their systems close to the textbook strength of the materials they use.
Magnetic deflected ballistic mass scales differently, and strength of materials is not as important as the strength of a uniform magnetic field. For large enough loops, a magnetic field permits unlimited velocities, though other considerations (control and spalling to name two) limit speeds to the rough order of 20 km/s . This means large magnetically deflected systems can store hundreds of times as much energy per mass, and the mass can be cheap steel rather than expensive carbon fiber. Lets look at the math for that:
|
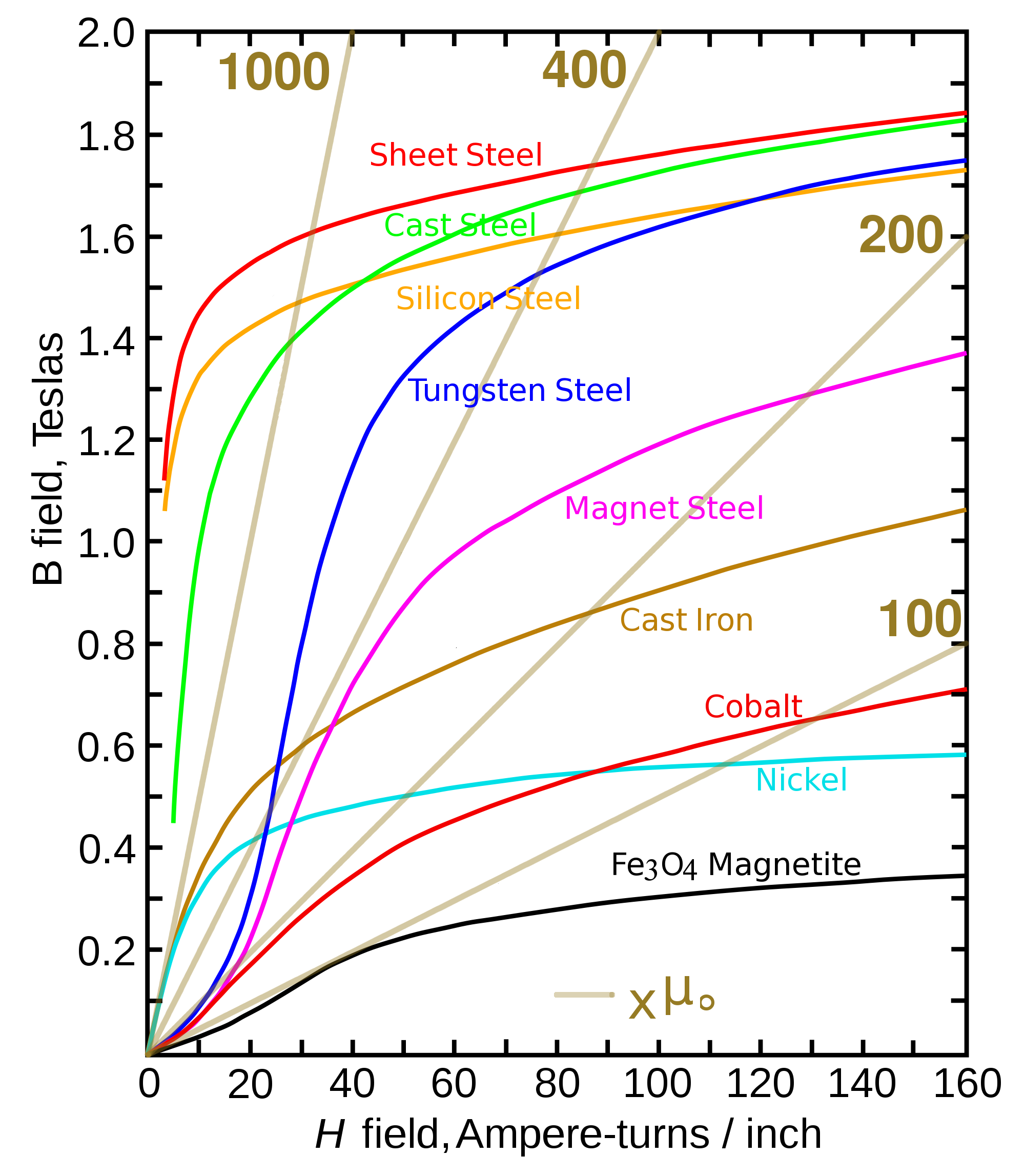
The pressure exerted by a magnetic field in a local area is the flux density B ( in Tesla, kg/Coulomb-sec ) squared divided by twice the permeability of free space μ ( 4 π × 1e-7 kg m / Coulomb2 ). The magnetic pressure p (as distinct from power P ) is p = B2/2μ in Pascals. Magnetic fields form closed circuits - the flux entering a region must leave it again. The flux entering the moving rotor of a power loop must travel back out in a closed path. The maximum flux in steel approaches 1.7 tesla; 1 tesla is a reasonable engineering maximum. If field is stitching in and out of the iron rotor, from magnet poles running longitudinally inside the circumference of the rotor, perhaps half the surface is at maximum field strength, so the average pressure might be approximately 0.5 / π 8e-7 = 200 KPa. This is much lower than the tensile strength of carbon fiber ( perhaps 1.7 GPa ), but the mass density of the field is zero (OK, OK, from special relativity it is 2 picograms per cubic meter, but a lot lighter than 1700 kilograms per cubic meter for carbon fiber). This means there is no material limit on V2. |
A rectangular cross section iron rotor (density 8000 kg/m3) with height H and thickness T is under no longitudinal stress. It is easier to control if it is stiff and resists bending (make T larger), but it can operate at higher accelerations if the mass per area is small (T is small). A rotor 1 centimeter thick and a meter wide weighs 80 kg/m2 - at 200KPa it accelerates towards the magnet at a = 2.5 km/sec2. In a 1 meter radius loop, and with V2 = a R, then V is a paltry 50 meters per second. However, with a 25 meter radius loop, V is 250 meters per second, and with a 500 meter radius loop (the size of a pivot irrigator circle), V is 1100 meters per second. The energy E stored in a circular storage ring is E = ½ M V2 ; M = 2 π ρ R T H ; a = p / ρ T ; so E = π p H R2 . For the same magnetic field pressure p and cross sectional scale H, the energy stored goes up as the square of the radius R, while the cost of building the system (and the power losses in the electromagnets and controllers) goes up linearly with the radius.
Very large systems can store enormous amounts of energy. A 1 kilometer diameter loop with 1 meter cross section and average field pressure of 200KPa stores 1.6E11 Joules or 44 megawatt-hours. A 100 kilometer diameter loop stores 440 gigawatt-hours, while costing only 100 times as much. If we assume the system costs about $1000/meter (this seems high for a system mass produced in identical sections) the 100 kilometer diameter loop would cost about $300M, but it could store 10 hours of power from 40 1.1 GW nuclear plants costing $8 billion dollars each. In other words, it could peak load level base load power plants costing 1000 times as much.
If the day/night cost difference for power was 2 cents per kilowatt-hour (it is much higher now, before massive peak load leveling) and the 100km diameter storage ring operated at 25% capacity (selling 110 GWh once a day) it would produce $2.2 million a day. It would pay off its investment in less than 5 months. More importantly, it would greatly improve the economic viability of any power plant connected to it, moving daylight solar power to nighttime, night time wind power to daytime, and baseload power to any time of day, as well as store power to move into and out of long distance power lines at whatever rates those power lines can handle.
This massive "spinning reserve" could satisfy whatever "spike" demands a regional grid might produce, from the sudden off-line failure of a power plant or transmission line, to an unforeseen heat wave or cold snap.
Power Handling Electronics
With one significant caveat. Power will be put into and out of the rotor with variable speed linear motors, so power must be converted in frequency from the kHz speeds of the linear motors to the DC or 60Hz AC of the power network. Converting power at these speeds is not free - switching power electronics costs from $10 to $100 per kilowatt (if you can do so cheaper, you can make lots of money right now selling less expensive PC power supplies!). At $10/kilowatt, the 100km storage ring may cost $300M, but the linear motor electronics to move 20 GW in or out might cost an additional $500M. This will need further study. However, very similar costs are encountered in most power storage systems, and improvements developed for any of them will have industry-wide benefits.
Drag
If the magnetic field is absolutely uniform, there is no magnetic drag. Drag occurs when the field changes in time in a conductor (or changes over distance into a moving conductor). A changing magnetic field induces an electric field, and an electric field causes currents in the conductor. The fields will change, making control adjustments to the trajectory of the rotor, but with good measurement and control programs these control changes will be small.
Like the flywheel cousin, a magnetically levitated rotor will operate in high vacuum. At CERN, in a similar vacuum chamber, we move particles at close to the speed of light, with very little scattering and drag, because the vacuum is very good. A power storage rotor does not need nearly as good a vacuum. However, we will need a very good system to deal with leaks. Unlike CERN, a major leak in a power storage ring can release a lot more energy (CERN's beam power is a mere freight train's worth). Further, a small particle can knock a larger chunk of mass off the rotor, which can knock even more mass off the wall, leading to a hypervelocity spalling cascade. This may limit the speed of the system. For the same magnetic pressure, we can increase rotor thickness and reduce velocity.
Earthquakes
Increasing rotor mass has consequences. The maximum accelerations encountered in a magnitude 9 earthquake may exceed 10m/s2 - one gee. Although that is a small fraction of the forces needed to deflect the rotor around turns, it does become significant if the rotor is massive and moving slowly. The next section discusses adding energy storage (without expensive turnaround magnets) by using long "straightaway" sections between semicircular end deflectors. While the straightaways can operate at much lower power and cost, they must be capable of controlling the rotor while being accelerated by earthquakes. Where the system crosses faults, the stationary track will need significant adjustable "sideplay" to accommodate shifts in entering and exiting tunnel. For this and other reasons, the systems may be easier to build in deep ocean water, where the inertia of the sea will protect floating tunnels while stopping the high speed shrapnel that might result from total system failure.
Scaling Power Loops
Smaller power loops will look like a racetrack oval. The radius of the D shaped ambits on the end will depend on the velocity squared, the magnetic field strength, and the width of the magnet poles. With the right geometries of coils and permanent magnets, the field strength can approach the saturation flux of the rotor iron, applied over many strips along the surface of a curved (or tubular) rotor. The spacing can be small - a millimeter or so - as long as variations in the spacing can be measured within a tiny fraction of that. A working rule of thumb derived from the launch loop, for a combination of permanent and copper coil magnet, is that the radius is proportional to the velocity squared divided by 14km/sec2.
Thus, a 1000 meter per second rotor will need a 70 meter radius, 140 meter diameter ambit. If the whole oval is 500 meters end to end, then the total length of the rotor is 1160 meters. If the rotor weighs 3 kilograms per meter, then it stores 1.5MJ per meter of kinetic energy, and the whole rotor stores 1.74GJ of energy - about 480 kilowatt hours.
If we double the speed to 2km/s, then the ambit diameter becomes 560 meters, 4 times the size. If we increase the oval length proportionally to 2000 meters, then a 3 kilogram per meter rotor stores 6MJ/m, and the whole rotor stores 27.8GJ, or 7.7 megawatt hours, 16 times the power of the previous example.
For "low" velocity loops, the energy goes up as the square of the linear dimensions, and presumably the square of the cost. Put differently, the cost goes up as the square root of the stored energy, at least until the velocity creates other problems.
There is some loss associated with length. We must hold the rotor up against gravity. However, gravitational support forces are much smaller than ambit forces, and the magnets will be correspondingly weaker and cheaper. Simpler as well, we do not need to build complex geometries to achieve the desired field strength, nor do we need to anchor against very high forces.. Rather than 14,000 meters per second squared, we must make 10 meters per second squared, and the cost per length of the magnets will be at least 140 times smaller. Let's assume that a meter of straight-away costs 100 times less than our ambits.
Thus, for our two examples above, the cost of the straightaway is 5% of the cost of the ambits, yet they store 5 times as much ballistic energy. Obviously, an optimal loop storage system should have very long straightaways. However, with a simple oval, the land cost will also go up with the straightaway cost. We can assume that the power loop is buried in tunnels for safety in case of failure, but access will still require an expensive easement.
Q-tip tracks
We can reduce the cost of the easement by turning the ambits somewhat more, into a "Q tip" shape. If we add an additional 45 degrees of turn, then 45 degrees of straightening out, then our easement will fit in about ten times the radius squared, with a long straight section of narrow easement in between. On land, that easement may fit under a straight railroad right-of-way. Finding two large patches of land next two a railroad right-of-way is probably not too difficult. The tunnels can be small bore - perhaps 50 centimeters - and dug with the same slant-drilling equipment used for fractured-shale gas fields. The tunnels around the end magnets will probably be much larger.
8 km/sec rotors
An interesting thing happens when the rotor speed is the same as orbital velocity - the rotor no longer needs to be supported against gravity. Earthquakes still pose a risk - we may need to move the rotor as much as 1 gee, both up and down and side to side, to match the Earth's movement, but the important point here is that earthquakes have limited duration - the coils and magnets need be energized only for a few seconds, or minutes for "500 year" earthquakes. The magnet controllers might heat up more than normal, but they do not normally consume much standing power.
Being able to run the rotor at near ballistic velocities of around 8 km per second means that we can go large distances with only second-order correction forces. Assume that the rotor velocity ranges between 9km/sec (full store) and 6 km/sec (empty store). Assume a straight section, under a railroad right-of-way, of 500 km, hopefully along a very straight right-of-way in the desert. The ambit radius is 5.8km, and the area of the easements is 330 square kilometers - large, but remember that we can sublet the easement for other uses, such as wheat fields or cattle ranching.
Such a large system may accommodate many rotors and tubes, perhaps packed together into a triangular array for most of their journey. A 1 meter diameter tunnel might carry 100 kilograms per meter of rotor. The available energy per meter is 0.5*100kg/m*(90002-60002 m/s) or 2.25 GJ/m. The whole system stores 2.25 Petajoules of available energy, or 625 Gigawatt hours. This can power the electrical grid of North America for one hour.
Assume the rotor is cylinders of structured iron, surrounded by a few percent by weight of strength-oriented carbon (pyrolitic? diamondoid? graphene?) to minimize the effects of hypervelocity spalling. Iron is about 140 dollars per ton - assume our mass produced cylinders are 1000 dollars per ton, one dollar per kilogram. One kilogram can store 225 megajoules of accessable energy, or 62.5 kilowatt-hours; at 6.5 cents per kWh industrial rates, that is $4 of electricity per kilogram, stored per cycle.
If the tunnel, track, and rotor cost $1000/meter, and store $400/meter worth of electricity, then we can pay for the storage system in a few power cycles - days or possibly weeks. Of course, the way the system will make money is on the differences between spot market lows and highs. If the spot market fluctuates daily between 4 cents/kWh and and 8 cents/kWh, and we can level that to between 5 cents and 6.6 cents on a national scale, then our profit is $100 per meter per day. We can pay for the storage system in a couple of weeks, after that, profit.
Large batteries may someday cost $200/kWh (they are more expensive now). Batteries corrode, have a limited lifetime, and can be as subject to catastrophic failure as power loop. Flywheels are more expensive ($300/kWh) but have longer service life. Pumped hydro can be as cheap as $10/kWh, but it is inefficient and sites are few and distant. Compare these to power loop at $1.60 per kWh for the regional facility described above.
International ocean scale storage will be far cheaper and even more profitable.
Efficiency
We will lose power with drag, magnet losses, and motor losses. Both magnet and motor losses are proportional to force, and only indirectly to velocity. Motor drive power is proportional to force times velocity - the faster we go, the smaller the ratio of motor loss to motor power. The bigger the loop, the less often we need to force the rotor to turn, relative to the time we are traveling mostly ballistically. The larger the diameter of the rotor, the less surface area exposed to residual gas. So very big loops, moving very fast around gentle turns, will be highly efficient, perhaps less than 1% loss per week, and less than 1% loss per input/output cycle. We can efficiently transport power around the globe, instead of losing 7% per 1000km in HVDC intertie systems.
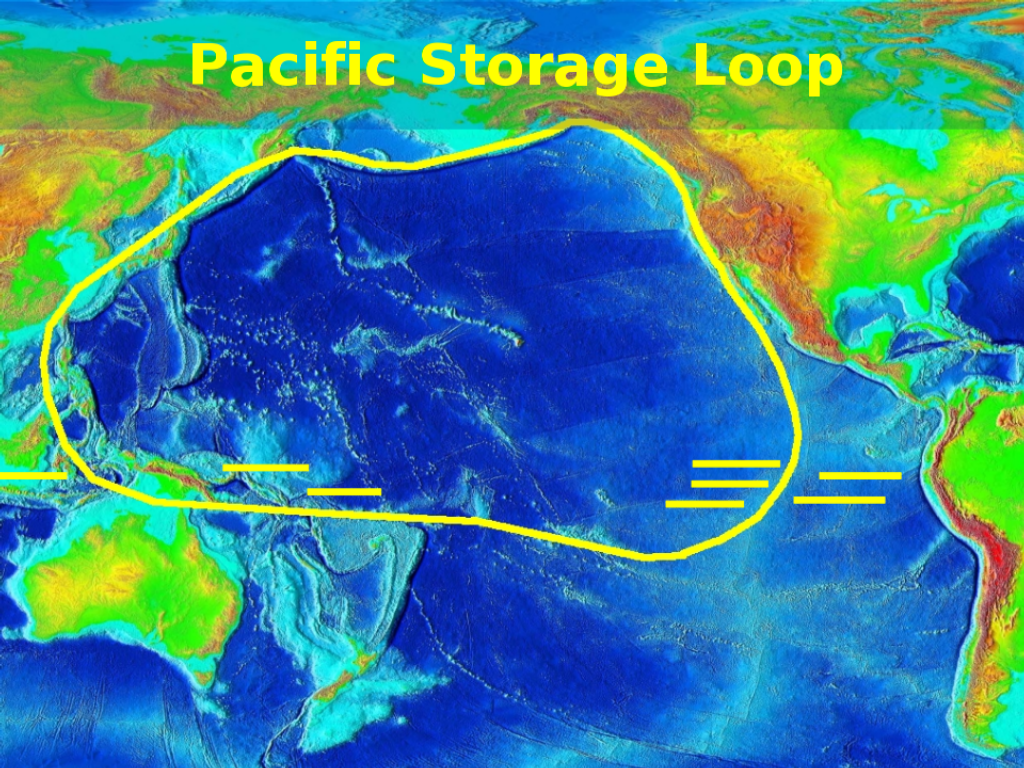
The Pacific Loop
Much larger systems are possible. Perhaps 4 billion people live around the Pacific rim, with a circumference of more than 30,000 kilometers. If the rotor and tube is deep underwater, far out on the edge of the continental shelf, the water can provide safety shielding. A system weighing 1000 kilograms per meter, and moving at 6 to 9 km/s, provides 187.5 Terawatt-hours of energy storage. At 10kW per person (first world consumption for all energy sources), this system will store almost 20 hours of power. More importantly, the power can be added or removed anywhere along the loop. It is 12 time zones across, permitting day-night spreading of peak load with high efficiency.
Similar loops could store power in all the oceans of the world - Indian, North and South Atlantic, Artic, and circum-Antarctic.
Many systems can coexist on similar tracks, perhaps separated by a kilometer or two (except at crossings), reducing the possibility of common mode failure and fratricide. It is conceivable that 10 such systems of loops could load-level the planet over an entire week. Of course, by that time we suffer many failures, and learn how to make the power loops very robust and safe. A 700 terawatt-day system, providing week-long power storage for 10 billion people using 10 kilowatts each, is conceivable by the end of this century.
This can load-level any source of energy, from steady-state nuclear plants to wind and solar systems with week-scale weather patterns. While space energy should be the long term goal (relieving the earth of damaging "green" energy harvesting systems), in the short term this will make any energy source more adaptable to daily, weekly, and hemispheric demand fluctuations.
If we use 10% of that power ( 10 TW ) for space launch, with 40% efficient launch loops to high orbits, we can launch 4000 metric tonnes per minute, or 840 million tons per year into space. This is about 10% of global ocean shipping, or about 4 times global air cargo. We can provide far more power with energy beamed from space, collected by mid-ocean receivers in one part of the world and sent to mid-ocean launch loops halfway around the globe.
Why is this essential for the launch Loop?
We need to develop technologies for the launch loop - control, vacuum, expansion joints, and surface coating. We also need to manufacture the components of a launch loop in huge quantities. We need ocean anchoring, navigation, security, construction, maintenance, worker transport, and many other systems. We must develop expertise in finance, make international treaties, develop broad consensus that such megasystems are broadly beneficial and worth protection. We need to demonstrate millions of safe operation hours, study failure, and improve reliability before above-surface systems are built, with their potential for throwing shrapnel anywhere on earth. We must learn to survive earthquakes. And we need to learn all the "unknown unknowns".
One of the main drivers for launch loops will be space power systems. The best place for space power collectors is in halo orbits around the earth-moon Lagrange range points, which will move through the sky over the lunar month, targeting and re-targeting different mid-ocean rectennas (the safest and least ecologically damaging place to put them). Ocean power loops are the best way to transport this power from rectennas to land, or to launch loop farms, also in mid-ocean.
If we have large power loops in place, and the factories to build more, then launch loops can be built mostly from established infrastructure and demonstrated technologies. The risk is reduced, the cost is reduced, social acceptance is increased, and investment funds will spend less time at risk. Imagine trying to develop rocket technology without an existing aircraft industry, factories, and development centers.
From Goddard's first liquid fuel rocket (1923) to the Moon landing (1969) was 46 years. From Lilienthal's 1891 gliders, 78 years. Aluminum manufacturing, cryogenics, and other material developments were equally vital. These developments take time, and other profitable markets to pay for their development.
Hugely profitable power storage will develop mature technology very close to launch loop capability, without costing space investors a dime. The urgent need and the high profits will develop this capability much faster - decades, not generations. If there was infinite investment money for spaceflight, intermediate stages would not be necessary - we could support many paths to the goal, and break a lot of hardware and risk lives doing so. Military expenditures do that - the US spent 4 trillion dollars to develop ICBMs. Since launch loops, space elevators, orbital rings, and other hypothetical launch infrastructure systems are far more vulnerable than an ICBM in a hardened silo, they are lousy military investments.
Beacon Power flywheels: (Richard Muller "Energy for Presidents")
- 2500 pound ( 1130kg ) carbon fiber flywheels
- 5000 pound "container"
$1.30/kW-h
- 1500 mph ( 670.56 m/s )
- 30 W-h/lb ( 240KN/kg )
- 30 MN/kg power loop iron, 125x better
- 10 ft tall, 6 ft diameter
- 25 kW-h of energy
- 200 units at Stephentown NY
- 20MW total