Ultra High Apogee Transfer Orbits

A work in progress; I will add material about interplanetary mission assembly orbits Real Soon Now.

• Inclination Plane Change from Ultra High 1500000 km Apogee Orbits

• Inclination Plane Change from 200000 km Apogee Orbits

• Useless for Surprise Weapons Delivery

• Lunar "slingshot" boost

Error: The claims below about apogee changes to reach orbits in the equatorial plane are incorrect. To change from an inclined orbit to an equatorial orbit requires ΔV where the orbit crosses the equatorial plane. Assuming launch along a parallel latitude, the original orbit crosses the equatorial plane at both "semi-latus rectum"s, at a radius that is the geometric mean of apogee and perigee. So, an optimum maneuver might look something like: tilt the high apogee orbital plane so it crosses the equatorial plane at a high radius, then apply delta V at the crossing to flatten the orbit into the equatorial plane. I will figure out optimizations and write about them Real Soon Now.

High Apogee Orbits

Launch loops are not limited by the Tsiolkovskii exponential. High rotor velocities require large radius ambit magnets and vertical deflection magnets. However, the main difference between an 8 km/s launch and an 11 km/s launch is doubled energy cost (electrical power, not cryo-fuel) and somewhat reduced payload size, not an exponentially larger loop.

Hence, Earth orbits with very high apogees are slow, but not expensive to get to. Small velocity changes at high apogee translate to large velocity changes at lower perigees. If a project can tolerate the delivery delay, payload transfer via a high apogee orbit can save propellant, while ejecting exhaust at Earth escape velocity.

In 2022, we (fallaciously) assume an infinite supply of propellant, and an Earth orbit environment with an infinite capacity for exhaust. Bad assumption. Perhaps a less wasteful approach will conserve resources and preserve the space environment into the distant future.

For this discussion, L1 refers to the distance of the Earth-Sun L1 (or L2) point, about 1.5 million kilometers from Earth. I propose that as the maximum distance for manageable Earth orbits, without solar gravitational perturbations causing insurmountable control problems. The Kepler orbit velocity for a circular, 1.5 million kilometer diameter two-body Earth orbit is 515 m/s, and the period is 810 hours, while the three-body orbit including the Sun is 8766 hours and the "velocity" is 48 m/s. An object in a highly elliptical Earth orbit will pass through the ES L1 point between these two velocities, and the orbit will get distorted with each pass

We will ignore these solar gravity complications for this discussion, though they are actually opportunities for clever orbit design and payload delivery with less delta V than suggested here. With accurate measurement and thrust control, orbital mechanics is a very high precision endeavor; clever orbit designers with ample time can outperform brute force.

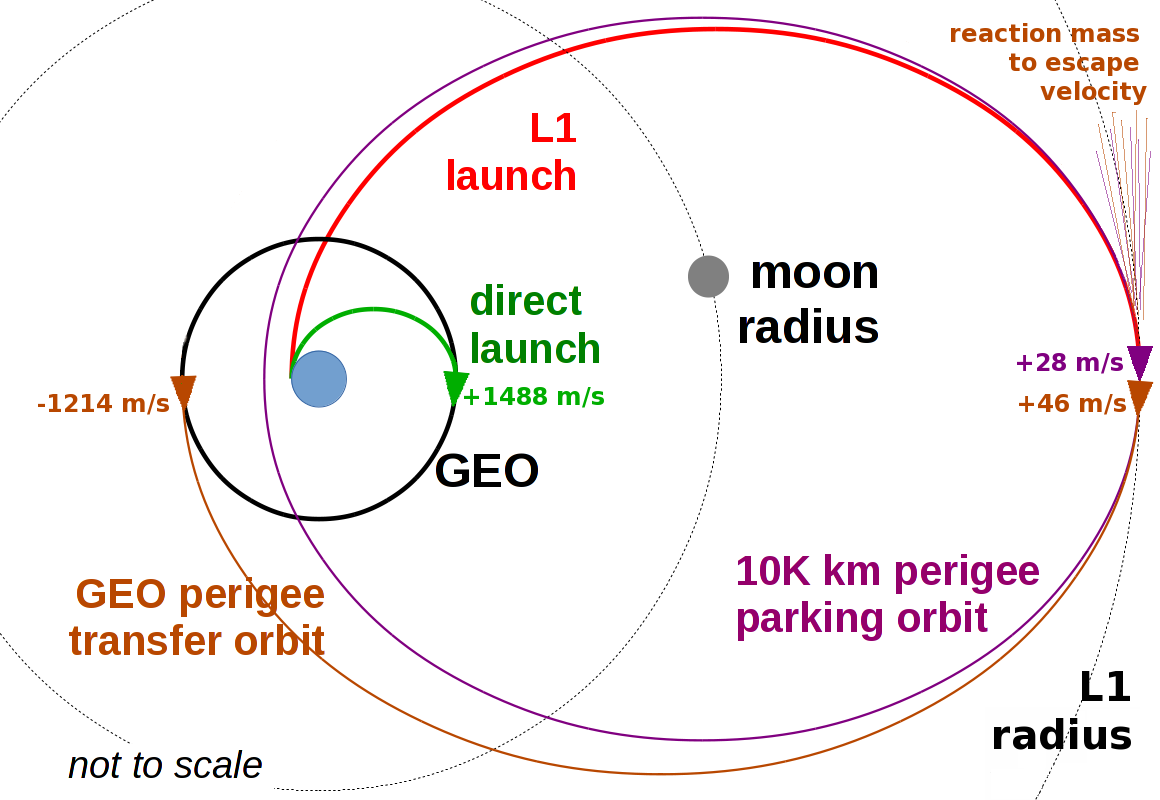
From 100 km altitude (6478 km radius, ignoring residual atmospheric drag and J₂ oblateness), the launch and insertion velocities are:

The last line differs from the others; that is a mission that involves a loop launch to L1 radius apogee, then a 28 m/s of delta V to raise perigee from loop radius to a 10,000 km perigee parking orbit. Later, after many orbits and synchronization (matching arrival time AKA true anomaly) with the GEO destination, add another 46 m/s thrust to raise perigee to GEO radius. Adding this angular momentum and velocity is cheap at high apogee radius. Indeed, the velocity change may be achieved naturally, without reaction mass thrust, from clever use of the 4-body problem (vehicle to Earth, Sun, and Moon).

After these manuevers, the vehicle GEO/perigee velocity is 4288 m/s; it must shed angular momentum and velocity to enter circular GEO orbit (V circular = 3075 m/s), unlike a vehicle arriving in an elliptical orbit from the loop at Earth, which has an apogee velocity at GEO of 1587 m/s and must gain angular momentum and 1488 m/s of velocity to enter circular GEO orbit.

Confusing openoffice spreadsheet here.

What if we could transfer angular momentum from L1 vehicle traffic to direct-from-launch vehicle traffic?

Imagine a tapered rotating tether at GEO, which can capture vehicles launched directly from Earth (adding delta V and angular momentum to the arriving vehicle) or from an L1/GEO transfer orbit (subtracting delta V and angular momentum from an arriving vehicle). If the ratio of the mass streams is 1214 to 1488 (23% more vehicle mass arriving via an L1 apogee), then no makeup momentum or thrust needs to be added at GEO. This assumes elliptical equatorial-plane orbits that "kiss" GEO; with additional radial velocity, we may be able to balance rotating tether angular momentum at GEO as well (this needs further study).

So, no additional delta V added for direct upward vehicles. About 74 m/s delta V added at L1 apogee for indirect-via-L1 vehicles.

L1 "orbit" is about 300 m/s sidereal relative to the Earth, faster than an isolated orbit without the Sun's gravitational influence. Vehicles in Earth orbit with perigees at that radius will return to Earth, though solar and lunar gravitational perturbations will be significant. The actual orbit and delta V must be computed and adjusted for every individual mission. On the other hand, we can probably manage the object cloud to minimize collisions and maximize launch rates throughout the day, month, and year. Some of the vehicles will make many orbits before arriving at GEO; these will be unmanned cheap cargo orbits. Given that payloads today sometimes wait years for orbital slots, launching them into orbit cheaply for eventual delivery (perhaps months later) may be a cost-effective tradeoff - better late than never!

Rocket exhaust emitted at L1 will leave the Earth-Moon system at much higher than escape velocity, and end up in solar orbit with an aphelion at Earth's solar radius and a perihelion a few million kilometers closer to the Sun, in a slightly shorter period orbit than the Earth itself. Since the material is emitted in the equatorial plane, not the ecliptic plane, it will not be coplanar with the Earth's solar orbit, crossing the plane only twice per hear. After a few hundred years, the exhaust might pass through the Earth/Moon system system again; chances are, it will be perturbed by Jupiter and scattered far too thinly to detect. I dislike wasting mass (probably argon from a VASIMR engine) that way, but there won't be much of it.

For extra bonus points, presume a high exhaust velocity and a huge shipping rate, calculate the argon loss rate, and compare that to the production rate of atmospheric argon via natural potassium 40 radioactive decay. Is this "billion year sustainable"?

Inclination Plane Change from Ultra High Apogee Orbits

Launch loops are in fixed locations, and cannot rotate azimuth with respect to the Earth. The loop is assumed to be aligned parallel to the equator at 8° south latitude, south of San Diego and east of French Polynesia. All launches from the loop will be into orbital planes tilted by 8° with respect to the equator. The Earth turns, on an axis tilted 23.5° with respect to the ecliptic plane, so over the course of a sidereal day the orbit plane orientation will change ± 8° with respect to the equator, and the sidereal launch azimuth will rotate 180° . That offers many mission possibilities, but it does NOT allow direct launch into an arbitrary high inclination or retrograde Earth orbit. Without a plane change, apogee will always be 8° north of the equator.

However, plane changes are relatively easy at a very high altitude, low velocity apogee. Apogee velocity at 1.5 million kilometers distance from an loop launch at 100 km altitude is less than 50 m/s; with a 96 m/s retrofire thrust, the vehicle will orbit retrograde, and with a 124 m/s retrofire thrust, the result will be a retrograde orbit with a 10000 km radius (3600 km altitude) apogee.

Starting from an 8° inclination, a 62 m/s apogee thrust oriented 41° from retrograde will put the vehicle into a polar orbit with an atmosphere-grazing perigee (at 8° south). With an adequate heat shield, the vehicle can aerobrake by 3140 meters per second into a transfer orbit to a polar LEO orbit. A 42 m/s apogee thrust can put the vehicle into a 51.6° inclined orbit co-planar with the International Space Station.

The aero-braking maneuver can be spread out over multiple, with a few hundred meters per second lost on each pass. That can keep the heat shield temperature down, perhaps allowing a reusable non-ablative heat shield.

Reduced Apogee to High Inclination Orbits

However, the problem with these very high orbits is their very long period, almost 75 days. This conserves expensive reaction mass, but time is money, and so is heat shield mass. What if we choose a lower high apogee, say 200,000 km (4.7 times GEO radius), about half the distance to the Moon?

This is a 95.74 hour orbit, 4 sidereal days, almost 20 times quicker than the ultrahigh apogee orbit. However, all the apogee plane change velocities are multiplied by 7.1, so more propellant is needed. If the I_SP is 200 seconds, the propellant fraction is approximately 15% to ISS.

For a transfer to polar orbit, the plane change and ISS rendezvous propellant and entry heat shield can be delivered 4 sidereal days before the cargo vehicle.

MoreLater

MoreLater

Useless for Surprise Weapons Delivery

For either high or ultrahigh apogee orbits, the time between the plane change and Earth atmosphere entry is more than a day. The trajectory (and deviation from the filed flight plan) will be obvious to meter/day accuracy to any organization with an accurate radar; this will be useless for a surprise attack on a north-of-the-equator nation, especially since the perigee position (and aerobraking latitude) will remain 8 degrees south of the equator.

While this can be used for the construction of orbital weapons platforms, with proper pre- and post-launch inspections, it will be very difficult to create a threatening platform unobserved, while an intermediate range ground launch ballistic missile could easily destroy the platform if it orbits over hostile territory.

Space assets, and the launch loops that deliver them, may always be more vulnerable than accurate ballistic missiles in hardened silos. No sane national military organization will use launch loops to attack armed northern hemisphere targets. An internationalized orbiting weapons platform operated by the United Nations might be attacked by a "rogue nation", but that nation would not survive retaliation by all the rest of the UN orbiters.

On the other hand, I'm sure the Trilaterals or Illuminati or Republicans or Girl Scouts will end up in control of a UN orbiting weapons system, if there actually are such organizations with such intent. I dunno, it's hard to believe that Republicans actually exist

Lunar "slingshot" boost ?

A seeming alternative to high apogee transfer orbits (that doesn't actually work very well) is a slingshot orbit past the Moon, speeding up the vehicle at the expense of some lunar momentum. Unfortunately, the Moon is in an orbit with inclination varying from 18.3 to 28.6 degrees; it crosses the equatorial plane only twice a month, and the launch loop must be at a precise Earth-rotational angle to take advantage of that. A popular idea, but not very practical.