Differences between revisions 51 and 52

Trapezoid Bolt

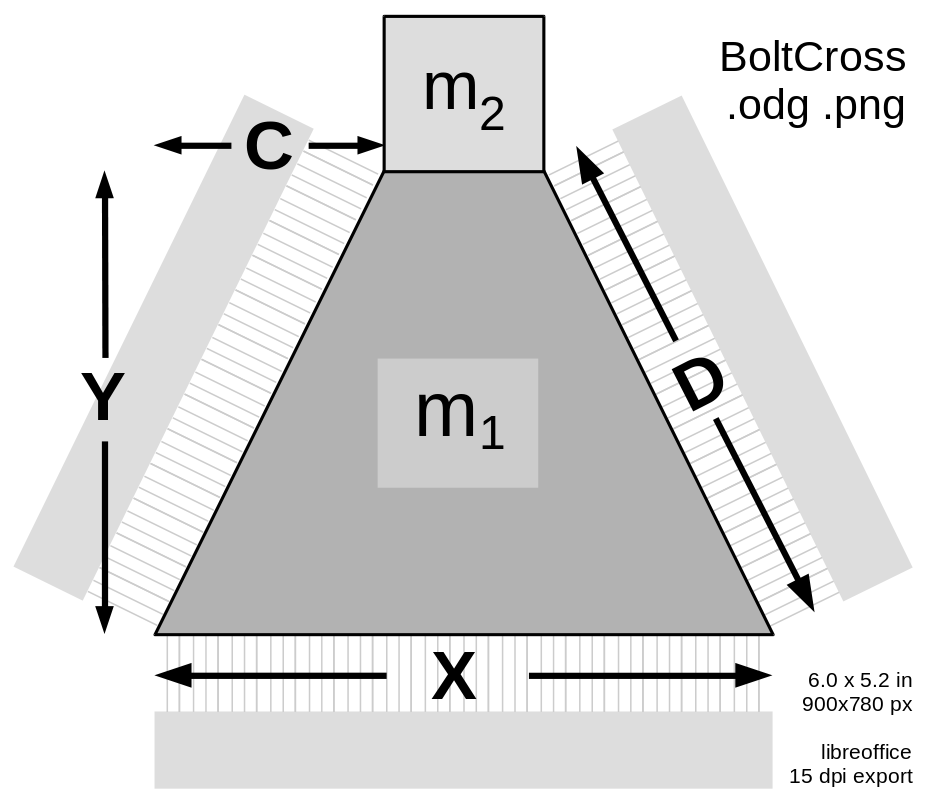
The launch loop rotor is composed of separable bolts, mostly made of thin laminations of transformer steel, along with carbon fiber stiffeners, embedded aluminum induction motor conductors, and a central spine. The bolts are normally used in two modes; assembled into a multilobed rotor for the main tracks and inclines, and separated into separate bolts for minimum radius deflection.

The number of lobes in the rotor (and the number of bolts in parallel) remains to be determined; probably between 4 and 6. The length of the bolts may also change. The size and cross section is constrained by the linear density of the rotor.

For a 4.32 kg/m rotor with six bolts arranged in a hexagon, each bolt will mass 7.2 grams per centimeter of length. If 30% of the bolt mass is non-iron mass m₂, and 70% of the bolt is m₁ then m₁ is approximately 5 g/cm = 5e-3 kg/m.

The density of 4% silicon transformer steel is 7.65 g/cm³, so A₁, the cross section of the area with mass m₁, is A₁ = 0.65 cm² = 6.5e-5 m². ~~~ A₁ = (X-C) × Y ~ so ~ Y = A₁ / (X-C) .

Deflection Mode

In deflection mode, an electromagnet pole (shown at the bottom of this diagram) pulls the rotor towards it, with near-saturation flux density B_{max} , perhaps 1.8 Tesla. The material will be strongly saturated and with considerable hysteresis at this field strength; that actually helps regulate the deflection force.

The deflection field "entering" at the bottom exits at the two diagonal pole faces, with less flux density. The (atttracting) deflection force at the bottom is F_X ~=~ X ~×~ B_{max}^2 / 2 \mu_0 so F_X = X × 1.29 MPa . The flux at each diagonal face is B_D = ( X / 2 D ) B_{max} so the force at each face is F_D ~=~ D ~×~ B_D^2 / 2 \mu_0 ~=~ D ~×~ (X/2D)^2 B_{max}^2 / 2 \mu_0 ~=~ X^2/D × B_{max}^2 / 8 \mu_0 so F_D = X²/D × 0.16 MPa .

Note that the flux B_D cannot exceed B_{max} , so D > X/2 . The bolt cannot be very thin in the Y direction.

A fraction C/D of that force is directed upwards for each face; the total upward force through both faces is F_C = 2 C (X/D)² × 0.16 MPa.

The angle of the faces can be computed from the geometry of the assembled rotor, and the stator wedge shape of the stator windings and the plenums penetrating it. If there are N lobes, and the stator wedges have an angle of W degrees, then the angle of both faces of the trapezoidal bolt are 360/N-W, and the angle on each face is half that, 180/N - W/2. Here's some plausible bolt face angles:

	Bolt face angles
W	N=3	N=4	N=5	N=6
0°	60°	45°	36°	30°
10°	55°	40°	31°	25°
20°	50°	35°	26°	20°
30°	45°	30°	21°	15°

Since D² = Y² + C² = (A₁/(X-C))² + C² , the total downward deflection force is:

\Large F_y ~=~ X \left( 1 - { { X ~~ C } \over { 2 \left( \left( {\LARGE { A_1 \over { X-C } } } \right)^2 + C^2 \right ) } } \right) { { B_{max}^2 } \over { 2 \mu_0 } }

This deflects mass m₁ + m₂, so the total radial acceleration is a_y = F_y/( m₁ + m₂ ), which we hope to maximize by optimizing X and C, given A₁.

MoreLater

-  ⇤ ← Revision 51 as of 2018-08-11 19:37:36 → 
  Size: 3597
  Editor: KeithLofstrom
  Comment:
+   ← Revision 52 as of 2018-08-11 19:40:09 → ⇥
  Size: 3534
  Editor: KeithLofstrom
  Comment:
-Deletions are marked like this.
+Additions are marked like this.
 Line 16:
-The angle of the faces can be computed from the geometry of the assembled rotor, and the stator wedge shape of the stator windings and the plenums penetrating it.   If there are N lobes, and the stator wedges have an angle of W degrees, then the angle of both faces of the trapezoidal bolt are 360/N-W, and the angle on each face is half that, 180/N - W/2.  Here's some plausible face angles:
+The angle of the faces can be computed from the geometry of the assembled rotor, and the stator wedge shape of the stator windings and the plenums penetrating it.   If there are N lobes, and the stator wedges have an angle of W degrees, then the angle of both faces of the trapezoidal bolt are 360/N-W, and the angle on each face is half that, 180/N - W/2.  Here's some plausible bolt face angles:
 Line 18:
+||        ||<-4>         Bolt face angles         ||
-Line 20:
+Line 21:
-||<)>  4° ||<)> 58° ||<)> 43° ||<)> 34° ||<)> 28° ||
||<)>  8° ||<)> 56° ||<)> 41° ||<)> 32° ||<)> 26° ||
||<)> 12° ||<)> 54° ||<)> 39° ||<)> 30° ||<)> 24° ||
||<)> 16° ||<)> 52° ||<)> 37° ||<)> 28° ||<)> 22° ||
+||<)> 10° ||<)> 55° ||<)> 40° ||<)> 31° ||<)> 25° ||
-Line 25:
+Line 23:
+||<)> 30° ||<)> 45° ||<)> 30° ||<)> 21° ||<)> 15° ||

Diff for "TrapezoidBolt"

Trapezoid Bolt

Deflection Mode