Differences between revisions 48 and 69 (spanning 21 versions)

Trapezoid Bolt

The launch loop rotor is composed of separable bolts, mostly made of thin laminations of transformer steel, along with carbon fiber stiffeners, embedded aluminum induction motor conductors, and a central spine. The bolts are normally used in two modes; assembled into a multilobed rotor for the main tracks and inclines, and separated into separate bolts for minimum radius deflection.

The number of lobes in the rotor (and the number of bolts in parallel) remains to be determined; probably 4 or 6. The length of the bolts also will be determined later; gaps between lengths will change with velocity, and the gaps will interrupt the motor field and cause some vibration in the vehicle sked. The size and cross section of the rotor is constrained by its linear density; the current estimate is 43.2 grams per centimeter of rotor length, or 4.32 kg per meter.

Rotor Mode

The angle of the faces can be computed from the geometry of the assembled rotor, and the stator wedge shape of the stator windings and the wedge-shaped stator winding gaps penetrating it. (Note 1) If there are N lobes, and the stator wedges have an angle of W degrees, then the angle of both faces of the trapezoidal bolt are 360/N-W, and the angle on each face is half that, θ = 180/N - W/2. Here's some plausible bolt face angles:

Stator Angle W	Bolt face angle θ
Stator Angle W	N=3	N=4	N=5	N=6
0°	60°	45°	36°	30°
10°	55°	40°	31°	25°
20°	50°	35°	26°	20°
30°	45°	30°	21°	15°

Deflection Mode

The radius of the ambit and upturn deflection magnets are constrained by acceleration, rotor mass density, and maximum deflection force. An electromagnet pole (shown at the bottom of this diagram) pulls the rotor towards it, with near-saturation flux density B_{max} , perhaps 1.8 Tesla. The material will be strongly saturated and with considerable hysteresis at this field strength; hysteresis helps regulate the deflection force, though it increases the controller power necessary to modify it.

For a 4.32 kg/m rotor with six bolts arranged in a hexagon, each bolt will mass 7.2 grams per centimeter of length. If 30% of the bolt mass is non-iron mass m₂, and 70% of the bolt is m₁, then m₁ is approximately 5 g/cm = 5e-3 kg/m.

The density of 4% silicon transformer steel is 7.65 g/cm³, so A₁, the cross section of the area with mass m₁, is A₁ = 0.65 cm² = 6.5e-5 m².

Given the face angle θ, the area A₁, and optimizing for D = X/2, we can compute the dimensions X, Y, and C.

~~~ A₁ = (X-C) × Y ~ so ~ Y = A₁ / (X-C) .

The widest, thinnest rotor iron is easiest to deflect, however, the flux on face X must exit through the two faces D, constraining minimum bolt iron height.

MoreLater

An electromagnet pole (shown at the bottom of this diagram) pulls the rotor towards it, with near-saturation flux density B_{max} , perhaps 1.8 Tesla. The material will be strongly saturated and with considerable hysteresis at this field strength; that actually helps regulate the deflection force.

The deflection field "entering" at the bottom exits at the two diagonal pole faces, with less flux density. The (atttracting) deflection force at the bottom is F_X ~=~ X ~×~ B_{max}^2 / 2 \mu_0 so F_X = X × 1.29 MPa . The flux at each diagonal face is B_D = ( X / 2 D ) B_{max} so the force at each face is F_D ~=~ D ~×~ B_D^2 / 2 \mu_0 ~=~ D ~×~ (X/2D)^2 B_{max}^2 / 2 \mu_0 ~=~ X^2/D × B_{max}^2 / 8 \mu_0 so F_D = X²/D × 0.16 MPa .

Note that the flux B_D cannot exceed B_{max} , so D > X/2 . The bolt cannot be very thin in the Y direction.

A fraction C/D of that force is directed upwards for each face; the total upward force through both faces is F_C = 2 C (X/D)² × 0.16 MPa.

Note 1: The spacing between hyperspeed rotor and the wire stator must be maintained actively by globally aware electronics. If the stator contacts the rotor in any channel anywhere along the 6000 km length of the rotor, the rotor and stator will be vaporized and the entire launch loop will fail. This is almost impossible, and will only become possible after years of development and high volume deployment of lower speed power storage loops. Technology evolves, and intermediate evolutionary steps and accumulated experience is required. Spacing control will require redundant electronics, and some means of rapidly withdrawing short sections of stator outwards from the bolt stream if any anomalies are detected.

MoreLater

Since D² = Y² + C² = (A₁/(X-C))² + C² , the total downward deflection force is:

\Large F_y ~=~ X \left( 1 - { { X ~~ C } \over { 2 \left( \left( {\LARGE { A_1 \over { X-C } } } \right)^2 + C^2 \right ) } } \right) { { B_{max}^2 } \over { 2 \mu_0 } }

This deflects mass m₁ + m₂, so the total radial acceleration is a_y = F_y/( m₁ + m₂ ), which we hope to maximize by optimizing X and C, given A₁.

MoreLater

-  ⇤ ← Revision 48 as of 2018-08-10 20:58:23 → 
  Size: 2770
  Editor: KeithLofstrom
  Comment:
+   ← Revision 69 as of 2018-08-12 23:54:58 → ⇥
  Size: 5477
  Editor: KeithLofstrom
  Comment:
-Deletions are marked like this.
+Additions are marked like this.
 Line 4:
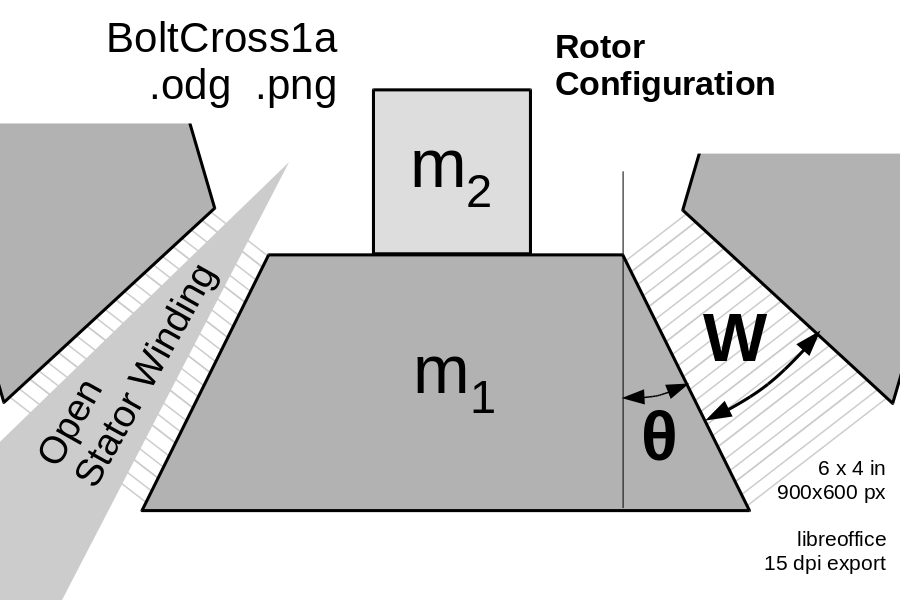
-|| [[ attachment:BoltCross.png | {{ attachment:BoltCross.png | | width=300 }} ]] || The launch loop rotor is composed of separable bolts, mostly made of thin laminations of transformer steel, along with carbon fiber stiffeners, embedded aluminum induction motor conductors, and a central spine.  The bolts are normally used in two modes; assembled into a multilobed rotor for the main tracks and inclines, and separated into separate bolts for minimum radius deflection.<<BR>><<BR>>The number of lobes in the rotor (and the number of bolts in parallel) remains to be determined;  probably between 4 and 6.  The length of the bolts may also change.  The size and cross section is constrained by the linear density of the rotor.<<BR>><<BR>> For a 4.32 kg/m rotor with six bolts arranged in a hexagon, each bolt will mass 7.2 grams per centimeter of length.  If 30% of the bolt mass is non-iron mass m₂, and 70% of the bolt is m₁ then m₁ is approximately 5 g/cm = 5e-3 kg/m. <<BR>><<BR>>The density of 4% silicon transformer steel is 7.65 g/cm³, so A₁, the cross section of the area with mass m₁, is A₁ = 0.65 cm² = 6.5e-5 m². $~~~$ A₁ = (X-C) × Y $~$ so $~$ Y = A₁ / (X-C) . ||
+The launch loop rotor is composed of separable bolts, mostly made of thin laminations of transformer steel, along with carbon fiber stiffeners, embedded aluminum induction motor conductors, and a central spine.  The bolts are normally used in two modes; assembled into a multilobed rotor for the main tracks and inclines, and separated into separate bolts for minimum radius deflection.

The number of lobes in the rotor (and the number of bolts in parallel) remains to be determined;  probably  4 or 6.  The length of the bolts also will be determined later; gaps between lengths will change with velocity, and the gaps will interrupt the motor field and cause some vibration in the vehicle sked.  The size and cross section of the rotor is constrained by its linear density; the current estimate is 43.2 grams per centimeter of rotor length, or 4.32 kg per meter.

== Rotor Mode ==

The angle of the faces can be computed from the geometry of the assembled rotor, and the stator wedge shape of the stator windings and the wedge-shaped stator winding gaps penetrating it. (Note 1)  If there are N lobes, and the stator wedges have an angle of W degrees, then the angle of both faces of the trapezoidal bolt are 360/N-W, and the angle on each face is half that, θ = 180/N - W/2.  Here's some plausible bolt face angles:

||<|6> [[ attachment:BoltCross1a.png | {{ attachment:BoltCross1a.png | | width=350 }} ]] ||<)|2>Stator<<BR>>Angle<<BR>>W||<:-4> Bolt face angle θ ||
||<)> N=3 ||<)> N=4 ||<)> N=5 ||<)> N=6 ||
||<)>  0°   ||<)> 60° ||<)> 45° ||<)> 36° ||<)> 30° ||
||<)> 10°   ||<)> 55° ||<)> 40° ||<)> 31° ||<)> 25° ||
||<)> 20°   ||<)> 50° ||<)> 35° ||<)> 26° ||<)> 20° ||
||<)> 30°   ||<)> 45° ||<)> 30° ||<)> 21° ||<)> 15° ||
-Line 8:
+Line 21:
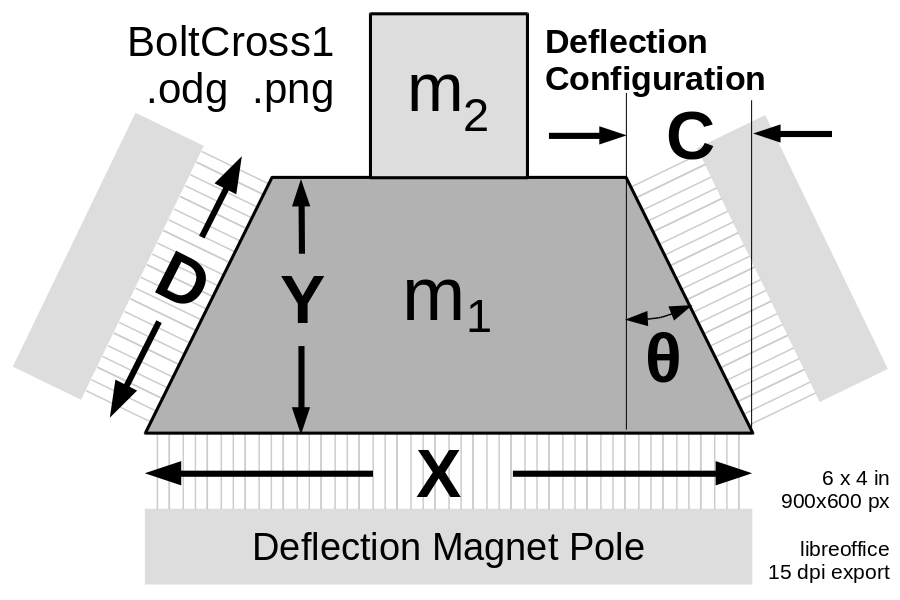
-In deflection mode, an electromagnet pole (shown at the bottom of this diagram) pulls the rotor towards it, with near-saturation flux density $ B_{max} $, perhaps 1.8 Tesla.  The material will be strongly saturated and with considerable hysteresis at this field strength;  that actually helps regulate the deflection force.
+The radius of the ambit and upturn deflection magnets are constrained by acceleration, rotor mass density, and maximum deflection force.
An electromagnet pole (shown at the bottom of this diagram) pulls the rotor towards it, with near-saturation flux density $ B_{max} $, perhaps 1.8 Tesla.  The material will be strongly saturated and with considerable hysteresis at this field strength; hysteresis helps regulate the deflection force, though it increases the controller power necessary to modify it.

For a 4.32 kg/m rotor with six bolts arranged in a hexagon, each bolt will mass 7.2 grams per centimeter of length.  If 30% of the bolt mass is non-iron mass m₂, and 70% of the bolt is m₁, then m₁ is approximately 5 g/cm = 5e-3 kg/m. <<BR>><<BR>>The density of 4% silicon transformer steel is 7.65 g/cm³, so A₁, the cross section of the area with mass m₁, is A₁ = 0.65 cm² = 6.5e-5 m². 

|| [[ attachment:BoltCross1.png | {{ attachment:BoltCross1.png | | width=350 }} ]] || Given the face angle θ, the area A₁, and optimizing for D = X/2, we can compute the dimensions X, Y, and C.<<BR>><<BR>>$~~~$ A₁ = (X-C) × Y $~$ so $~$ Y = A₁ / (X-C) . <<BR>><<BR>>The widest, thinnest rotor iron is easiest to deflect, however, the flux on face X must exit through the two faces D, constraining minimum bolt iron height.<<BR>><<BR>>MoreLater ||

An electromagnet pole (shown at the bottom of this diagram) pulls the rotor towards it, with near-saturation flux density $ B_{max} $, perhaps 1.8 Tesla.  The material will be strongly saturated and with considerable hysteresis at this field strength;  that actually helps regulate the deflection force.
-Line 12:
+Line 32:
-Note that the flux B_D cannot exceed B_{max}, so D > X/2 .  The bolt cannot be very thin in the Y direction.
 
A fraction C/D of that force is directed upwards for each face; the total upward force through both faces is F,,C,, = 2 C (X/D)² × 0.16 MPa. Since D² = Y² + C² = (A₁/(X-C))² + C²  , the total downward deflection force is:
+Note that the flux $  B_D $  cannot exceed $ B_{max} $ , so $  D > X/2 $  .  The bolt cannot be very thin in the Y direction.

A fraction C/D of that force is directed upwards for each face; the total upward force through both faces is F,,C,, = 2 C (X/D)² × 0.16 MPa.







Note 1:  The spacing between hyperspeed rotor and the wire stator must be maintained actively by globally aware electronics.  If the stator contacts the rotor in any channel anywhere along the 6000 km length of the rotor, the rotor and stator will be vaporized and the entire launch loop will fail.  This is '''''almost'' impossible''', and will only become possible after years of development and high volume deployment of lower speed power storage loops.  Technology evolves, and intermediate evolutionary steps and accumulated experience is required.  Spacing control will '''require''' redundant electronics, and some means of rapidly withdrawing short sections of stator outwards from the bolt stream if any anomalies are detected.  


MoreLater

Since D² = Y² + C² = (A₁/(X-C))² + C²  , the total downward deflection force is:
-Line 18:
+Line 51:
 This deflects mass m₁ + m₂, so the total radial acceleration is a,,y,, = F,,y,,/( m₁ + m₂ ), which we hope to maximize by optimizing X and C, given A₁.

Diff for "TrapezoidBolt"

Trapezoid Bolt

Rotor Mode

Deflection Mode