|
Size: 2489
Comment:
|
Size: 2566
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 14: | Line 14: |
| A fraction C/D of that force is directed upwards for each face; the total upward force through both faces is F,,C,, = 2 C (X/D)² × 0.16 MPa. Since D² = Y² + C², the total radial deflection force is: | A fraction C/D of that force is directed upwards for each face; the total upward force through both faces is F,,C,, = 2 C (X/D)² × 0.16 MPa. Since D² = Y² + C² = (A₁/(X-C))² + C² , the total downward deflection force is: |
| Line 16: | Line 16: |
| $$ \Large F_r ~=~ X \left( 1 - { { X C } \over { 2 ( Y^2 + C^2 ) } } \right) { { B_{max}^2 } \over { 2 \mu_0 } } $$ | $$ \Large F_y ~=~ X \left( 1 - { { X C } \over { 2 ( (A_1/(X-C))² + C² + C^2 ) } } \right) { { B_{max}^2 } \over { 2 \mu_0 } } $$ |
| Line 18: | Line 18: |
| This deflects mass M₁ + M₂, so the total radial acceleration is a,,r,, = F,,r,,/( M₁ + M₂ ), which we hope to maximize. | This deflects mass m₁ + m₂, so the total radial acceleration is a,,y,, = F,,y,,/( m₁ + m₂ ), which we hope to maximize by optimizing X and C, given A₁. |
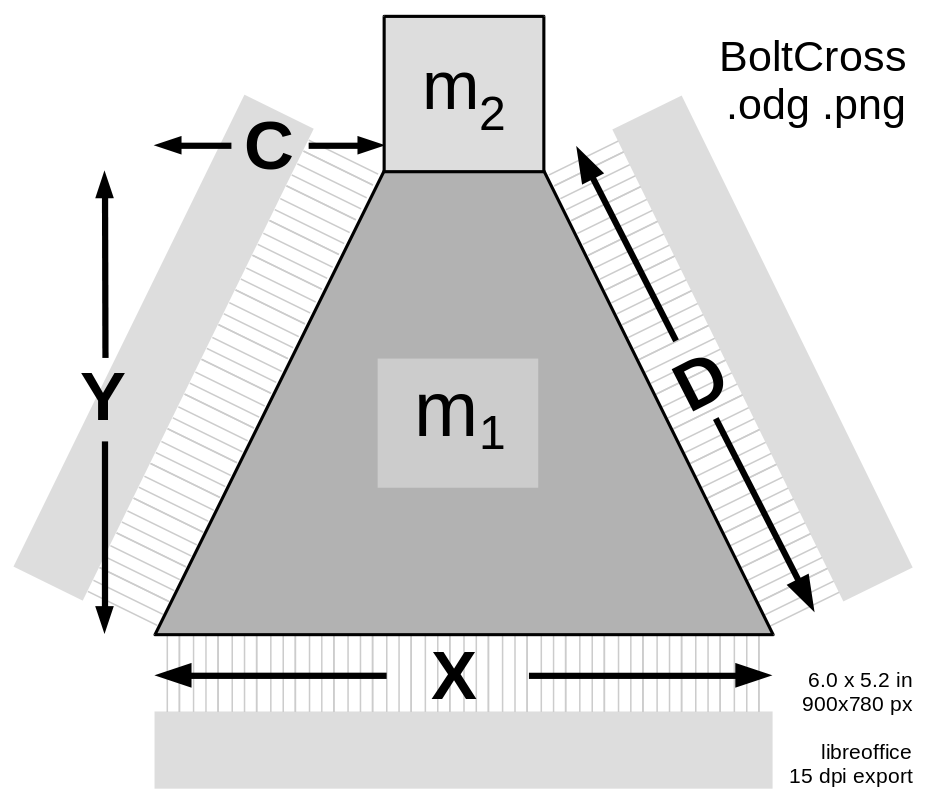
Trapezoid Bolt
The launch loop rotor is composed of separable bolts, mostly made of thin laminations of transformer steel, along with carbon fiber stiffeners, embedded aluminum induction motor conductors, and a central spine. The bolts are normally used in two modes; assembled into a multilobed rotor for the main tracks and inclines, and separated into separate bolts for minimum radius deflection. |
The density of 4% silicon transformer steel is 7.65 g/cm³, so A₁, the cross section of the area m₁, is A₁ = 0.65 cm² = 6.5e-5 m².~~~ A₁ = (X-C) × Y and Y = A₁ / (X-C) .
Deflection Mode
In deflection mode, an electromagnet pole (shown at the bottom of this diagram) pulls the rotor towards it, with near-saturation flux density B_{max} , perhaps 1.8 Tesla. The material will be strongly saturated and with considerable hysteresis at this field strength; that actually helps regulate the deflection force.
The deflection field "entering" at the bottom exits at the two diagonal pole faces, with less flux density. The (atttracting) deflection force at the bottom is F_X ~=~ X ~×~ B_{max}^2 / 2 \mu_0 so FX = X × 1.29 MPa . The flux at each diagonal face is B_D = ( X / 2 D ) B_{max} so the force at each face is F_D ~=~ D ~×~ B_D^2 / 2 \mu_0 ~=~ D ~×~ (X/2D)^2 B_{max}^2 / 2 \mu_0 ~=~ X^2/D × B_{max}^2 / 8 \mu_0 so FD = X²/D × 0.16 MPa .
A fraction C/D of that force is directed upwards for each face; the total upward force through both faces is FC = 2 C (X/D)² × 0.16 MPa. Since D² = Y² + C² = (A₁/(X-C))² + C² , the total downward deflection force is:
This deflects mass m₁ + m₂, so the total radial acceleration is ay = Fy/( m₁ + m₂ ), which we hope to maximize by optimizing X and C, given A₁.