|
Size: 1258
Comment:
|
Size: 1260
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 18: | Line 18: |
| $ {{\partial D}\over{\partial A}} ~ = ~ { { A({B^2}+{C^2}-{A^2}) } \over { 2 {C^2} D } } | $ {{\partial D}\over{\partial A}} ~ = ~ { { A({B^2}+{C^2}-{A^2}) } \over { 2 {C^2} D } } $ |
Stability
The main issue with stability is that perturbations exceeding a few millimeters from the ideal path ( as determined by ambient forces acting on the track ) cannot be corrected by track to rotor spacing alone. Given inaccurate force measurements, and track measurements, it is very easy for such perturbations to appear, indetectably.
Stability can be achieved by applying damping forces to the curvature, some constant \large { \partial \over { \partial t } } { { \partial^2 } \over { \partial L^2 } } ( L is the distance along the track ) added to the spacing forces. The big problem is measuring the curvature, which is exceedingly difficult to do for millimeter scale lateral displacements over track distances of tens of kilometers.
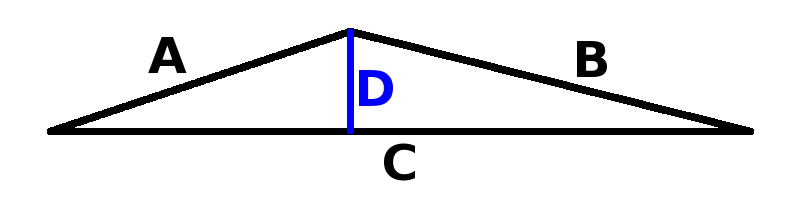
Suppose we are trying to estimate distance D from three precision measurements for A, B, C. We can compute D from this formula:
D ~ = ~ {\sqrt{2({A^2}{B^2}+{A^2}{C^2}+{B^2}{C^2})-({A^4}+{B^4}+{C^4})}\over{2C}}
The sensitivity of D to errors in A , B , and C is just the partials:
{{\partial D}\over{\partial A}} ~ = ~ { { A({B^2}+{C^2}-{A^2}) } \over { 2 {C^2} D } }
