Stability

Laser Distance Measurement Errors

The main issue with stability is that perturbations exceeding a few millimeters from the ideal path ( as determined by ambient forces acting on the track ) cannot be corrected by track to rotor spacing alone. Given inaccurate force measurements, and track measurements, it is very easy for such perturbations to appear, indetectably.

Stability can be achieved by applying damping forces to the curvature, some constant \large { \partial \over { \partial t } } { { \partial^2 } \over { \partial L^2 } } ( L is the distance along the track ) added to the spacing forces. The big problem is measuring the curvature, which is exceedingly difficult to do for millimeter scale lateral displacements over track distances of tens of kilometers.

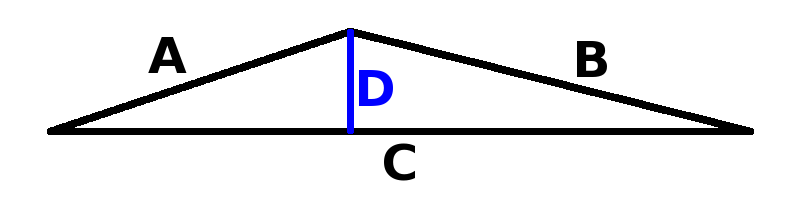
Suppose we are trying to estimate distance D from three precision measurements for A, B, C. We can compute D from this formula:

\large D = {\sqrt{2({A^2}{B^2}+{A^2}{C^2}+{B^2}{C^2})-({A^4}+{B^4}+{C^4})}\over{2C}}

The sensitivity of D to errors in A , B , and C is just the partials:

\large {{\partial D}\over{\partial A}} = { { A({B^2}+{C^2}-{A^2}) } \over { 2 {C^2} D } } ~ ~ ~ ~ \large {{\partial D}\over{\partial B}} = { { B({A^2}+{C^2}-{B^2}) } \over { 2 {C^2} D } } ~ ~ ~ ~ \large {{\partial D}\over{\partial C}} = { ({{A^2}+{B^2})-({C^2}+2{D^2}) } \over { 2 C D } }

If D is small, these partials are very large. Assume that A \approx B (but not the same!) and that C = 2A - \epsilon , and D << A . This is the case if we are measuring the center point on a wide, very shallow and approximately symmetrical triangle.

Our equations reduce to:

\large D \approx \sqrt { A \epsilon } ~ ~ ~ ~ \large {{\partial D}\over{\partial A}} \approx {{\partial D}\over{\partial B}} \approx {-{{\partial D}\over{\partial C}}} \approx { A \over { 2 D } }

What if D is about 1 cm, and A is about 100 km? Then the partials are all 5E5, which means a 20 nanometer error measuring A, B, or C results in a 1 millimeter error measurement in D. If there are independent \sigma = 1mm errors in each variable, the RMS error sum is \sigma = 1.7 mm . If we are using 3 such numbers to compute a curvature, we will be taking differences of twice the center minus the ends, resulting in an error sum of \sigma = 3.4 mm . So, an error of only (20 nm/100km) or 2e-14 in our distance measurement results in a 3.4 mm uncertainty in track position. If we computing the time derivatives of successive curvature measurements, attempting to compute a damping factor, the error is increased again, for a curvature velocity error of 4.9 mm/timestep .

If we are using laser interferometers through the atmosphere, especially turbulent atmosphere with moisture and haze (maybe clouds!), it is quite unlikely we can make such long baseline measurements with 1/20 wavelength accuracy. This is hard to do in a temperature controlled box inside a lab. So, even if the partial differential equations indicate a convergent solution, they imply that we can compute accurate partials from the data available. This is unlikely.

This problem is similar to Euler's column formula for a tall skinny compression member. If the column is too skinny, a very small load, a tiny fraction of the compressive strength, will buckle it. A mass stream compression member resembles an Euler column. The solution is similar - guy wires and trusses. Over a very limited correction range (a fraction of the track/rotor spacing), and with a perfectly transparent atmosphere, those "guy wires" and "trusses" can be accurate laser interferometers. However, real atmospheres with clouds and doppler-shifting air movements can mess up the interferometers. So, the laser equivalent of long guy wires are not available, except for calibration on clear calm days. Laser "truss-works" can only be expected to operate over small distances in thick clouds - they must be multi-spectral and use many redundant paths.

Wide Laser Truss

Assume a "laser truss" with a 20 meter spacing between the track and a truss wire, and laser beams pitched at alternating 45 degree angles, as well as co-linearly with track and truss wire. Assume the laser paths have a \sigma = 20 nm error. A = B = 28.28 meters, C= 40 meters, D = 20 meters . The sensitivities are

\large {{\partial D}\over{\partial A}} = {{\partial D}\over{\partial B}} = \sqrt{0.5} ~ ~ ~ {{\partial D}\over{\partial C}} = 0.5

The statistical sum of the three errors is ( \sqrt { 5 } / 2 ) \times 20nm = 22.4 nm ) . The curvature error over 100 kilometers is approximately the accumulated statistical error for 2500 track segments, and 2500 truss segments, about 1.6 \mu m . The center bulge has an RMS error of ( 100 km * 1.6 um ) / ( 8 * 20 m ) = 1mm . This is still somewhat large.

Let's add another level of truss, this time with 4 km pitches and 2 km distances. Over the 100 km stretch, there are 50 truss segments, with a total of 100 errors, and an RMS error of 0.22 microns. The bulge has an error of ( 100 km * 0.22 \mu m ) / ( 8 * 2000 m ) = 1.4 \mu m . Very small. Over a 2000 km launch track, the error is 20 * \sqrt{ 20 } larger, or 0.13 mm. For a more realistic 1um laser error, the curvature error is 2.5 mm. By operating N measurement trusses in parallel, we can increase redundancy and reduce error by a factor of \sqrt{ N } , so 30 trusses, with 25 functional and not blocked by weather, could reduce the error to 0.5 mm. Big laser trusses and truss averaging provide more accurate curvature measurement than small trusses.

Cables, actuators, etc.

If the system can tolerate curvature errors larger than the track-rotor spacing, larger measurement errors are allowable. The reason we need such tight tolerances in a track and rotor only correction system is that damping is gradual, and rotor perturbations travel a long distance. That can make the perturbation collide with an anti-perturbation of the track. On the large scale, the track and rotor must be very tightly coupled.

But we can "stiffen our column" by adding mechanical systems which can absorb and propagate lateral forces, such cable trusses and guy wires. But the real opportunity is adding dynamic elements that can modulate forces and shift the center of mass, such as moving actuators and adjustable guy wire tensioning, as well as propellers and shutters in the atmosphere. With properly designed measurement and feedback, these systems can appear much stiffer than passive material elasticities can provide. With good measurement, broadly distributed mass, and fast actuators, the system can converge on an estimated neutral position and remain there, even if there are fairly large residual errors in the measurements and control, and large deviations which cannot be corrected merely with spacing control.

MORE LATER