|
Size: 1097
Comment:
|
Size: 1956
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| #format jsmath |
|
| Line 6: | Line 8: |
| $ { \partial \over { \partial t } } { \partial^2 \over { \partial l^2 } } $ added to the spacing forces. The big problem is measuring the curvature, which is exceedingly difficult to do for millimeter scale lateral displacements over track distances of tens of kilometers. |
$\large { \partial \over { \partial t } } { { \partial^2 } \over { \partial L^2 } } $ ( $ L $ is the distance along the track ) added to the spacing forces. The big problem is measuring the curvature, which is exceedingly difficult to do for millimeter scale lateral displacements over track distances of tens of kilometers. |
| Line 9: | Line 10: |
| {{attachment:triangle_stability.png}} | {{attachment:triangle_distance.png|triangle distance| width=300}} |
| Line 13: | Line 14: |
| $ D ~ = ~ {{sqrt{2*(A^2B^2+A^2^C^2+B^2C^2)-(A^4+B^4+C^4)}}\over{2C} $ | $ \large D = {\sqrt{2({A^2}{B^2}+{A^2}{C^2}+{B^2}{C^2})-({A^4}+{B^4}+{C^4})}\over{2C}} $ |
| Line 17: | Line 18: |
| $ {{\partial D}\over{\partial A}} ~ = ~ $ | $ \large {{\partial D}\over{\partial A}} = { { A({B^2}+{C^2}-{A^2}) } \over { 2 {C^2} D } } ~ ~ ~ ~ $ $ \large {{\partial D}\over{\partial B}} = { { B({A^2}+{C^2}-{B^2}) } \over { 2 {C^2} D } } ~ ~ ~ ~ $ $ \large {{\partial D}\over{\partial C}} = { ({{A^2}+{B^2})-({C^2}+2{D^2}) } \over { 2 C D } } $ If D is small, these partials are very large. Assume that $ A \approx B $ (but ''not'' the same!) and that $ C = 2A - \epsilon $, and $ D << A $. This is the case if we are measuring the center point on a wide, very shallow and approximately symmetrical triangle. Our equations reduce to: $ \large D \approx \sqrt { A \epsilon } ~ ~ ~ ~ $ $ \large {{\partial D}\over{\partial A}} \approx {{\partial D}\over{\partial B}} \approx { A \over { 2 D } } $ MORE LATER |
Stability
The main issue with stability is that perturbations exceeding a few millimeters from the ideal path ( as determined by ambient forces acting on the track ) cannot be corrected by track to rotor spacing alone. Given inaccurate force measurements, and track measurements, it is very easy for such perturbations to appear, indetectably.
Stability can be achieved by applying damping forces to the curvature, some constant \large { \partial \over { \partial t } } { { \partial^2 } \over { \partial L^2 } } ( L is the distance along the track ) added to the spacing forces. The big problem is measuring the curvature, which is exceedingly difficult to do for millimeter scale lateral displacements over track distances of tens of kilometers.
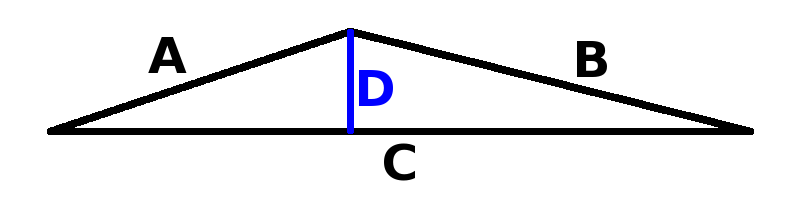
Suppose we are trying to estimate distance D from three precision measurements for A, B, C. We can compute D from this formula:
\large D = {\sqrt{2({A^2}{B^2}+{A^2}{C^2}+{B^2}{C^2})-({A^4}+{B^4}+{C^4})}\over{2C}}
The sensitivity of D to errors in A , B , and C is just the partials:
\large {{\partial D}\over{\partial A}} = { { A({B^2}+{C^2}-{A^2}) } \over { 2 {C^2} D } } ~ ~ ~ ~ \large {{\partial D}\over{\partial B}} = { { B({A^2}+{C^2}-{B^2}) } \over { 2 {C^2} D } } ~ ~ ~ ~ \large {{\partial D}\over{\partial C}} = { ({{A^2}+{B^2})-({C^2}+2{D^2}) } \over { 2 C D } }
If D is small, these partials are very large. Assume that A \approx B (but not the same!) and that C = 2A - \epsilon , and D << A . This is the case if we are measuring the center point on a wide, very shallow and approximately symmetrical triangle.
Our equations reduce to:
\large D \approx \sqrt { A \epsilon } ~ ~ ~ ~ \large {{\partial D}\over{\partial A}} \approx {{\partial D}\over{\partial B}} \approx { A \over { 2 D } }
MORE LATER
