Spaceport Torque
Roger Arnold's Spaceport captures incoming vehicles at perigee and accelerates them (while it decelerates). The vehicles arrive at a fraction of Spaceport orbital velocity and speed up to orbital velocity as the Spaceport slows down. The spaceport is moving slightly faster than circular orbital perigee in the beginning, and thus has a small net-upward acceleration, which we will ignore for now.
For ease of calculation, we will assume the spaceport has a perigee velocity v_p = 8000 m/s, the vehicle arrives at 4000 m/s, and gee at altitude is a = 10 m/s² (it is 8.9 m/s² at 310 km equatorial altitude, but let's keep this simple). The vehicle acceleration a_v within the spaceport is assumed to be 5 gees or 50 m/s², or 5 a. The spaceport is assumed symmetrical around its center of mass, extending a distance -L towards the inlet and +L towards the terminus. The vehicle mass is M and the spaceport mass is 2 m L >> M , with mass evenly distributed along its length.
The stopping distance is 2 L = {v_p/2}^2 / ( 2 a_v ) so L = {v_p}^2 / ( 16 a_v ) = {v_p}^2 / ( 80 a ) = 80 km. The total length and stopping distance is 2 L or 160 km. We will arbitrarily assign the datum at the center, so the entry point at t = 0 is x = -L . The velocity of the vehicle is v = 4000 + 50 t and the acceleration to 8000 m/s takes 80 seconds. The distance is the integral of this velocity added to -80000m, so d = -80000 + 4000 t + 25 t^2 .
The vehicle "lift acceleration" relative to the Spaceport at perigee is a_l = ( v^2 - {v_p}^2 )/ r_p where r_p is the Liftport perigee radius and v_p is the perigee velocity. A liftport begins vehicle capture at the perigee of a slightly elliptical orbit; the momentum transferred to the vehicle reduces Liftport apogee.
If vehicles descending from the Moon are the main source of makeup momentum, they may arrive weeks apart, as the Moon is in a slow inclined orbit that crosses the liftport orbital plane twice a month. Hence, the Liftport must store a lot of momentum, for weeks. Either the Liftport apogee (and perigee velocity) is somewhat high, or it must be massive, or capture rates are limited, or it must burn a lot of rocket propellant; all these options are inconvenient.
So; a_l is significant, and negative, until the vehicle accelerates to Liftport velocity v_p at the far end. The vehicle is constrained by the Liftport track, so instead of accelerating radially, it pushes radially on the track with a force of F = m a_l . The force is highest at the entry, half as high at the midpoint, and zero at the end. The vehicle spends 70% of its decelleration time on the second half of the track, but the radial force is much smaller. Obsessive readers are invited to derive v(t), {a_l}(t), and the distance down the track l(t), then compute the time integral of the torque on the liftport:
Torque = \int ~ m ~ {a_l}(t) ~ l(t) ~ dt . The integral which will be a fifth order polynomial in time. It will not be zero. The result will be a Liftport rotating away from the metastable "horizontal: orientation. Without immediate makeup thrust, it will keep turning and accelerating until it turns vertical, the keeps turning until it is backwards. Oops. If you don't believe this, please do the math yourself. It is better to find a better solution to the problem, and do the math for that, rather than determine exactly how inadequate this one is.
A better solution will look more complicated, but should help with three problems:
(1) zero net torque for vehicle capture, rotation to initial position when the vehicle stops
(2) provide positive stability, maximum at the desired pitch
(3) enhance lateral rigidity
. . . (3) requires some explanation. The Spaceport 2.0 description assumes couplers that adjust spacings to simulate an "einsteinium rigid" beam. If the perturbations are small, the coupler forces are small. However, keep in mind that the spaceport is quite long compared to its cross section; end torques are amplified at the couplers by the ratio of the length divided by the cross section. So, for a 80 km length and an 8 meter cross-section, the torques (and forces) at the center are multiplied by 10,000; if a 10 tonne vehicle vibrates at 10% of 5 gees, that is 50,000 Newtons wagging the ends, and 500 meganewtons at the couplers. To make a 1 millimeter length adjustment at the coupler with that force loading would require half a megajoule.
There's a reason why bridges are built with deep box frames, or suspension cables! Civil engineers may seem conservative, but they design structures that endure. Modern civil engineers are quite proficient in active damping; Japanese building engineers use piston actuators, and elevator movement(!), to help stabilize buildings in earthquakes.
|
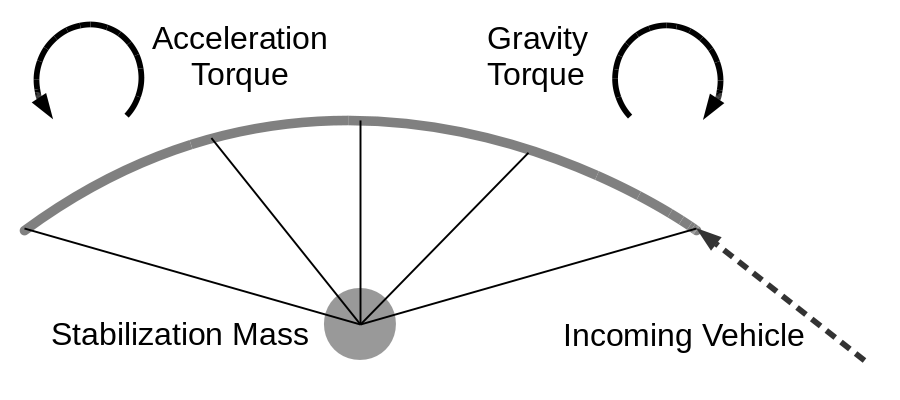
- Here's one hypothetical configuration for Spaceport 2.1 with a hanging counterweight. |
While this shows the vehicle approaching from the right, in the fixed-star inertial frame, the Spaceport is orbiting towards the right, overtaking the vehicle moving half as fast towards the right.
The drawing above is representative, by no means exact. The stabilization mass may hang further down; there will be many more cables and the webbing between them complex, the curve will be different and probably assymetrical. The important point is that the structure will be turned clockwise by gravity torque as before, but the vertical spacing is large enough for the acceleration force times the lever arm to create (on average) an opposing torque. That, combined with the gravitational torque as the structure turns, should add up to zero net rotation and zero angular velocity when the payload stops, relative to the Earth below.
The cables will presumably be actively lengthened and shortened during a capture. The relative speed of the vehicle begins at 4000 m/s in the example above; that is approximately the "speed of sound" of the cables as well. So, optimum control of cable tension and length will be determined by predictive computational modelling, not by real-time measurement and immediate feedback.
Spaceports and Launch Loops
With a launch loop providing orbital velocity, a Spaceport can be much simpler and easier to use, oriented vertically and correcting orbital eccentricity only.
Imagine a launch loop with an 80 km exit altitude (6458 km radius) and a target orbit at 400 km altitude or 6778 km radius. The target orbit velocity (ignoring Earth rotation) is v = \sqrt{ \mu / r } = \sqrt{ 398600.4418 km³/s² / 6778 km } = 7.6686 km/s. The angular momentum is v × r = \sqrt{ \mu × r } = \sqrt{ 398600.44 km³/s² × 6778 km } = 51978 km²/s.
The trick is to launch vehicles from the launch loop with the same angular velocity; with a launch altitude of 6458 km, that is a launch velocity (perigee) of v_p = 8.0486 km/s. We can compute the transfer orbit semimajor axis using this equation:
\large a = { \LARGE 1 \over { \huge { { 2 \over r_p } - { v_p^2 \over \mu } } } } = 6794.64 km.
The transfer orbit eccentricity e = 1 - r_p/a = 0.04954. After much complication, we can compute the radial (not tangential!) velocity at the destination , 0.0778 km/s or 77.8 m/s . Actually ±77.8 m/s; the transfer orbit passes through the destination orbit both outwards and inwards. And that is the Spaceport optimizing feature; we can use a vertical, gravity stabilized Spaceport, at a vastly lower velocity, capturing half the loop-launched vehicles upwardly bound, half downwardly bound ... though we might have to wait a while for the launch loop to line up both ways. Since the perigee is at only 80 km, in relatively dense atmosphere, the vehicle does not get to complete an orbit for this simple case.
So, we are only capturing at 77.8 m/s; we do not need to capture at 5 gees, or even the 3 gees of a launch loop. Let's limit the acceleration to 10m/s² - further, let's restrict the "jerk" to 10m/s³, allowing one second to ramp acceleration up and down. Total acceleration time, 8.8 seconds. Total acceleration length, less than 400 vertical meters. 20% of the peak acceleration and 0.5% of the length of a horizontal high speed Spaceport. Indeed, this will be a gentler ride and much easier to build than a passenger elevator in the Burj Khalifa skyscraper. Except for some precision rendezvous thrusters, this trip to LEO can be completely rocket-free.
How High Can We Go ?
Without using rockets, the highest elliptical orbit we can launch to has a perigee velocity just below escape velocity, which is \sqrt{ 2 \mu / r_p } = 11.11 km/s . The maximum angular momentum is \sqrt{ 2 \mu × r_p } = 71752 km²/s, which is also the angular momentum of a circular orbit with radius 2 × r_p or 12916 km . A useful orbit ( Server sky thinsats will orbit at 12789 km) but the extremely slow climb to apogee will be excruciating.
However, if we add a small amount of rocket thrust, we can reduce the wait a little, and reach much higher orbits. What we want is angular momentum, and the cheapest (though slowest) way to add angular momentum is at the apogee of a very high orbit.
We will target a geostationary orbit destination, and get there from a 300,000 km apogee, just inside the Moon's orbit. GEO radius is 42164 km, and circular orbit velocity is 3.0747 km/s . The angular momentum is 129640 km²/s.
The launch orbit has an apogee velocity of 236.6 m/s ; pretty slow. If we add just 195.5 m/s of delta V at apogee, the resulting transfer orbit has the desired 129640 km²/s angular momentum. The radial velocity change crossing GEO is 495.5 m/s. This is much larger than the 77.8 m/s to access LEO; we will need a much taller Spaceport. If we limit to 30 m/s² (the launch acceleration of the launch loop) and ignore jerk, our GEO Spaceport is about 4.1 km tall; perhaps 5 km tall with reduced jerk. That's much more difficult than a Burj Khalifa elevator, but far less difficult than a 100,000 km space elevator cable. Still vertical, and still gravity stabilized.
The above discussion is predicated on a "one up, one down" equal mass and velocity flow and a vertical spaceport. A tilted spaceport and assymetrical mass flows may be more optimum, with priority material from Earth arriving quickly (with an angular momentum deficit), and bulk materials slowly accumulating angular momentum and arriving months later, both captured on different trajectories.
The above discussion also assumes rails; perhaps rendezvous with the end of a zipline deployed past a pulley and generator is easier to arrange.