Power Loop for SusTech Notes
Most of this information will be reworked into a paper and/or a poster
Flywheel Scaling
The fastest possible (non-magnetically deflected) flywheel is a thin hoop of material at maximum stress. Assume a thin flywheel hoop rotating around a vertical axis, with radius r , cross section A , made of a material with a mass density of \rho and maximum tensile strength S_{max} . The mass of the whole loop is 2 \pi r A \rho , and the volume is V = 2 \pi r A .
If the flywheel rotates at angular frequency \omega , the rim velocity v = \omega r , and the stored energy is
E = \pi r^3 A \rho \omega^2 . The maximum usable energy is a (hopefully large) fraction of that.
Consider a small element d\theta of the hoop, where \theta is the position around the loop. If the hoop is circumferential stress is S_c , then we can construct a force triangle where the deflection of the circumferential force is S_c A d\theta / 2 at each end, for a total centripedal force of S_c A d\theta . This is balanced by the centrifugal acceleration of the element, dM a = ( r A \rho d\theta ) ( \omega^2 r ) . So:
S_c A d\theta = r^2 A \omega^2 \rho d\theta
S_c = r^2 \omega^2 \rho
Approaching maximum stress, v^2 = r^2 \omega^2 < S_{max} / \rho . . . Plugging this into the stored energy equation, we get:
E = \pi r A \rho ( r^2 \omega^2 ) < \pi r A \rho ( S_{max} / \rho ) = \pi r A S_{max}
\large { E < {1 \over 2} V S_{max} } . . . half the hoop volume times the maximum tensile stress.
Real flywheels will have rotating structure that does not contribute to this strength, and flywheels thicker than a thin shell will have inner material at less than maximum stress and storing less than maximum energy. So the simple energy equation above is overoptimistic; if you include the container, the empty volume, the axial motor, the magnetic bearings, a decent safety factor, etc, then the maximum stored energy may be a small fraction of this maximum . The maximum rim velocity, hence the maximum energy per flywheel mass, is similarly constrained.
Beacon Power flywheel maximum speeds are 670 meters per second; perhaps in time they may learn how to reliably increase this to 1000 meters per second. This will require defect-free manufacturing, and careful attention to stress management around yarn ends and voids in the binder matrix of the carbon fiber materials. Also, the hoops will need enough radial stiffness (and damping!) so that small radial vibrations do not create increased stresses; that material adds little to the energy storage. I wish them the best of luck.
Magnetic Field Pressure
The "pressure" of a magnetic field is P = B^2/2\mu_0 , where B is the magnetic field in Teslas ( Kg /( Coul s ) ), and \mu_0 is the permiability of free space, \mu_0 = \pi \times 4e-7 ( Kg m )/Coul2. When you multiply all that out, you get Kg /( m s2 ), or Newtons / m2 or Joules / m3 .
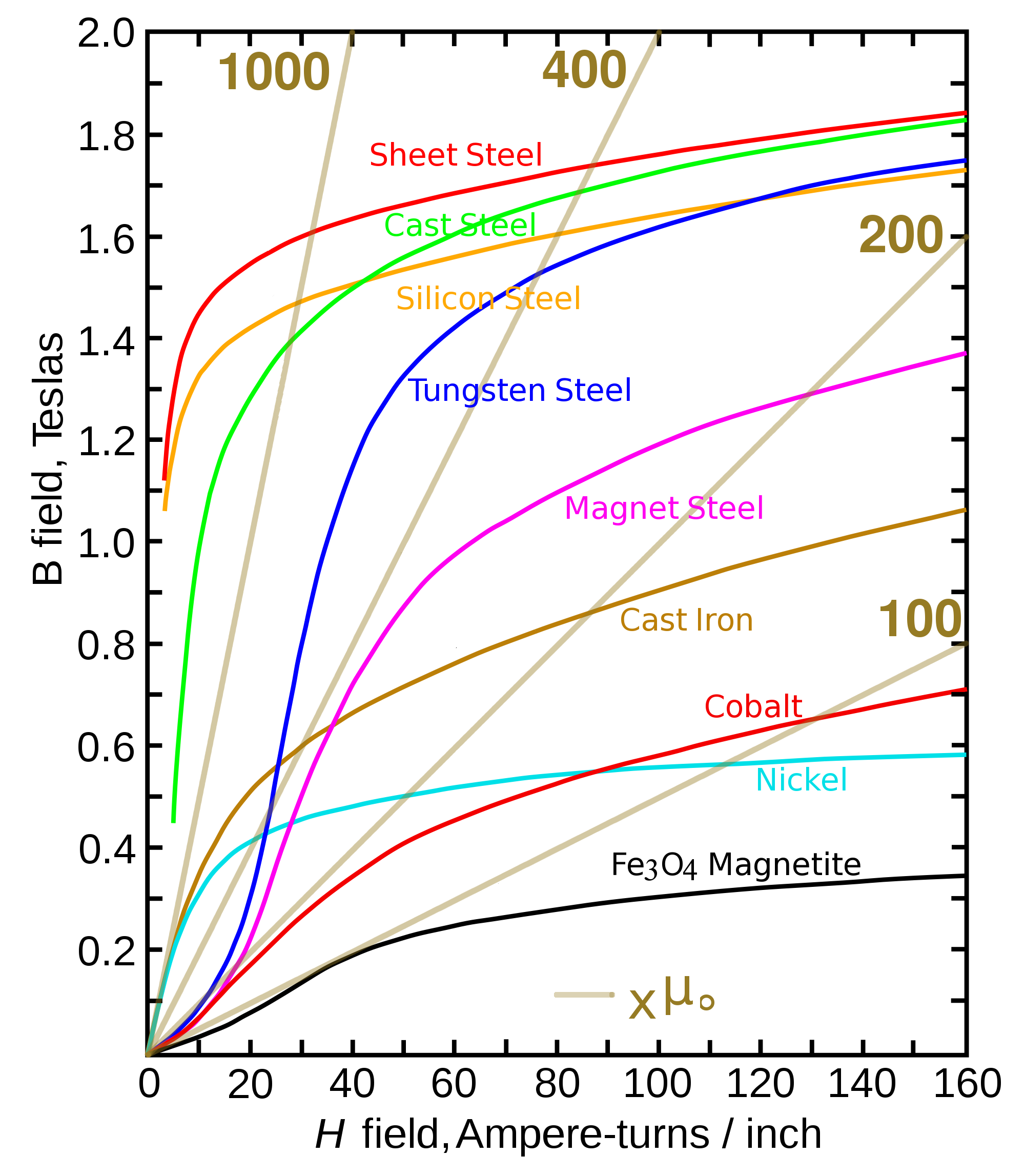
Ordinary steel saturates at magnetic fields approaching 2 Tesla, although significant extra "H" Amp-Turns/Meter magnetization is required to raise the field that high. |
Some might ask, why not use superconductors? Superconductors can generate high magnetic fields, but they are fragile in many ways. They require expensive and inefficient cooling, systems that can generate as much heat as the losses in copper magnet windings. The superconducting state is easily disrupted - when that happens, the stored energy in the field turns into resistive heating in the (former) superconductor. Heat capacity is very low for materials near absolute zero, so the regions near a fault can heat up explosively. When the field changes in a superconductor, the induced voltages push non-superconducting electrons in the material, creating resistive heating, also threatening a "quench" (explosive superconductor failure). There are plenty of other challenging problems to solve first - when you hear someone suggesting superconductors, run. They are dangerous to themselves and others.
"Attractive" magnetic pressure is unstable - Earnshaw's theorem. So a control system must continuously measure the gap and adjust the magnetic field with bandwidths of hundreds of kilohertz. Superconducting field windings for 60Hz generators have (so far) proved too difficult to deploy in weight-sensitive systems such as wind turbines. It is unlikely that practical 200 kHz superconducting control magnets will be available anytime soon.
Turning and Bending the Rotor with a Magnetic Field
Steel has a density ρ of approximately 8000 kg/m3. A rectangular cross section rotor (perhaps not the best shape!) with thickness t weighs 8000 × t kg/m2. A magnetic field generating pressure P N/m2 will deflect it with an acceleration a = P / \rho t . For a centimeter thick steel rotor and a 200,000 Pascal field pressure, the acceleration is 2500 m/s2. This is small compared to the acceleration in an advanced flywheel rotor (on the order of 500 km/s2) but it can be applied over a much larger radius, with static steel anchors to solid rock instead of spinning carbon fiber carrying the load.
A rotor moving at 1000 m/s deflected by a 2500 m/s2 acceleration turns 180° in a 400 meter radius (Shinkansen turns are 4000 meter radius). But the rotor does not need to spend the entire loop in a tight turn - long straightaways between the D shaped "ambits" at the end add energy storage without additional high acceleration magnets. On the straightaways, low acceleration magnets (10m/s) are needed to hold the rotor up against gravity, as well as deflect it to follow the ground movements of an earthquake. In the worst case, the ground can shear during an earthquake, and in the aftermath the rotor must be deflected around the new shear until it can be drained of energy and the tunnel re-aligned.
Unlike a flywheel inside a steel cylinder, a power loop rotor can travel down a vacuum tunnel deep in the ground. When (not if) the power loop fails, shrapnel will not reach the surface, though in the worst case it can tear up magnets and linear motors. Failing rotors can be designed to fracture and spill into side passages away from the deflection magnet; that can be messy, but most of the structure is ready to be repaired, loaded with a new rotor, and put back in operation.
Perhaps the best place to build larger, higher speed power loops is in floating steel tubes adjustably anchored to the sea floor. Seawater is better at stopping a runaway rotor than laboriously prepared "rotor dump caverns" underground, and water is far easier to tunnel through than rock. At least part of a large rock tunnel will encounter underground water, anyway, at similar pressures to an undersea tunnel. However, since many places where we want to store power (wind farms in New Mexico, for example) are far from the ocean, we may choose to put loops in narrow canyons and fill those with water, rather than dig tunnels.
Bending a rotor in a very large arc is not a problem. A t = 1 centimeter thick, h = 20 centimeter high rotor has a bending moment of inertia I = t3 h / 12, or 6.67e-7 m4. Young's modulus for steel E is 200 GPa, so the bending moment at the ends EI/r is 333 Newton-meters. Given a centripedal magnet deflection force of 40,000 newtons per meter, this is a tiny reshaping of the first few centimeters of the deflection magnet.
Relative Efficiency
Magnet power loss is proportional to current squared, and magnetic pressure is also proportional to current squared, so power loss is proportional to force. If the acceleration in the ambit magnets is 2500 m/s2, and acceleration between them on the straightaways is 10 m/s2 (gravity, approximately), then the dissipation of 1 kilometer of straightaway is approximately the same as 4 meters of ambit magnet. More efficient energy storage uses long straightways and few turns. We can combine straightways under one right-of-way, perhaps a power line, railroad, or freeway, by adding some extra radians of bend to construct a path shaped more like a "Q-tip" than a racetrack. For a long distance track it is reasonable to assume perhaps 10 radians of turn, rather than the 2π radians of a simple racetrack.
Thus our 1000 meter per second, 400 meter radius system might have 4000 meters of turning magnet, and and 20 kilometers of straightaway, if the ends are 10 kilometers apart. The turnarounds for this "short" system consume 50 times the power of the straightaway.
This example power storage rotor is 24 kilometers long and weighs 16 kilograms per meter. Moving at 1000 meters per second, it stores about 200 gigajoules, 50 megawatt-hours. While this is 10 times the energy storage capacity of the largest flywheel facility, it is inadequate to load level the wildly fluctuating power output of a large regional windfarm, much less approach the diurnal demand variation of the United States.
Scaling
Power loop systems have both the advantage and the drawback that the energy stored is proportional to the square of their dimensions. If we scale all the track lengths in the previous example by two, then we store four times the power. Holding cross section and acceleration constant, v^2 = a r ; if ambit radius r doubles, so does the velocity squared, and the kinetic energy per meter of rotor does also. If the rotor length also doubles (and the loss power doubles as well), then the energy stored goes up by a factor of four while the power loss and system construction cost only doubles. While the first demonstration power loops will be small and inefficient (and less economical than flywheels), as they scale to regional dimensions they will become more cost effective.
How big can we go? We can use a 30 kilometer radius ambit to deflect a 2 centimeter thick by 1 meter high rotor (80kg/m) moving at 8000 meters per second. If two straightaways are 500 kilometers, and with 10 radians of total deflection, the overall system length is 1300 kilometers. The energy storage capacity of one loop is 3.3e15 joules, about 0.9 terawatt-hours. If we cycle between 3000 and 8500 meters per second we can recover about the same amount of energy. Average US electrical use in 2010 was about 500 gigawatts, and total primary power production was 2.3 terawatts, so we would need about 60 of these very large loops to store two days of total primary energy production. This would not support an "all-alternative" US through two days of sparse wind and solar, but it would allow us to add significantly more of those chaotic sources to the grid without destabilizing it.
An interesting thing happens at 8000m/s ; that is approximately orbital velocity. This means that if the rotor follows the curvature of the earth, the centrifugal acceleration balances the gravitational acceleration, and the power loss for straightaway support is greatly reduced.
However, even if we design the system as reliably as we know how, even able to tolerate local control and magnet failures and small breaches of the vacuum containment, a large system will have more points of failure than a small system, and its loss from the power network will have more significant effects. We probably don't want to build power loops so big that the unexpected failure of five or six at once will seriously jeopardize the stability of the grid. Since the biggest common mode source of error is bad theory, as implemented in replicated software, we should not only have many systems, we should encourage them to use multiple designs and multiple sets of control software, perhaps by increasing the insurance premiums for "monocrop" deployments. Those who disagree and favor "strength in numbers" should contemplate the 2008 banking crisis, and the Poisson distribution.
Stability