Orbit Circularization

What is the ΔV needed for apogee insertion into a circular equatorial orbit from a launch loop transfer orbit, and for perigee insertion from a space elevator transfer orbit?

The destination orbit has a radius of r_d and a velocity of v_d = \sqrt{ \mu / r_d } were \mu = 398600.4418 km³ / s².

---

Simple Case, Equatorial Orbits

---

The launch loop calculation is fairly simple.

An 80 kilometer breech altitude launch loop defines a transfer orbit with a perigee r_p = 6378 + 80 km = 6458 km . The semimajor axis is a = 0.5 * ( r_p + r_d ) , the eccentricity e = ( r_d - r_p ) / ( r_d + r_p ) , the characteristic velocity is v_0 = \sqrt{ \mu / ( a * ( 1 - e^2 ) ) } , and the apogee velocity is v_a = ( 1 - e ) v_0 . Combining and simplifying:

{v_a}^2 = ( 1 - e )^2 {v_0}^2 = ( \mu / a ) ( 1 - e )^2 / ( 1 - e^2 )

{v_a}^2 = ( 2 \mu r_p ) / ( r_d ( r_d + r_p ) )

v_a = \sqrt{ ( 2 \mu r_p ) / ( r_d ( r_d + r_p ) ) }

\Delta V = v_d - v_a

---

The space elevator calculation is more complicated.

For transfer orbits below geosynchronous, the apogee of the orbit is the release radius r_a , and the angular velocity is \omega_E = 2 \pi / P_{sidereal} , where P_{sidereal} is the sidereal day, 86164.0905 seconds. We want to find r_a and the perigee velocity v_p . We will have to work backwards.

v_a = \omega_E r_a

{v_a}^2 / 2 \mu = 1 / r_a - 1 / ( r_a + r_p )

Solve for r_p , perigee radius, the candidate r_d

r_p = \Large { r_a \over { \Large { { \huge { 2 \mu } \over { {r_a}^3 {\omega_E}^2 } } } - 1 } }

That's a 4th order polynomial in r_a, and there are com= licated[[ https://en.wikipedia.org/wiki/Quartic_function | analytical formulas for the roots of that, but it is easier to guess and test with a speadsheet.

So, a 20 iteration binary search of r_a between 29700 km and 53000 km will converge r_p on our target r_d

The numbers are approximate; the space elevator will not stay perfectly vertical, but will swing back and forth, oscillate longitudinally, etc. Lunar and solar tides will displace the counterweight, payload releases will change the tension on the tether, and many other complications can change the numbers above by a fraction of a percent. In production use, a space elevator tether must be measured and modelled to estimate the best release altitude.

---

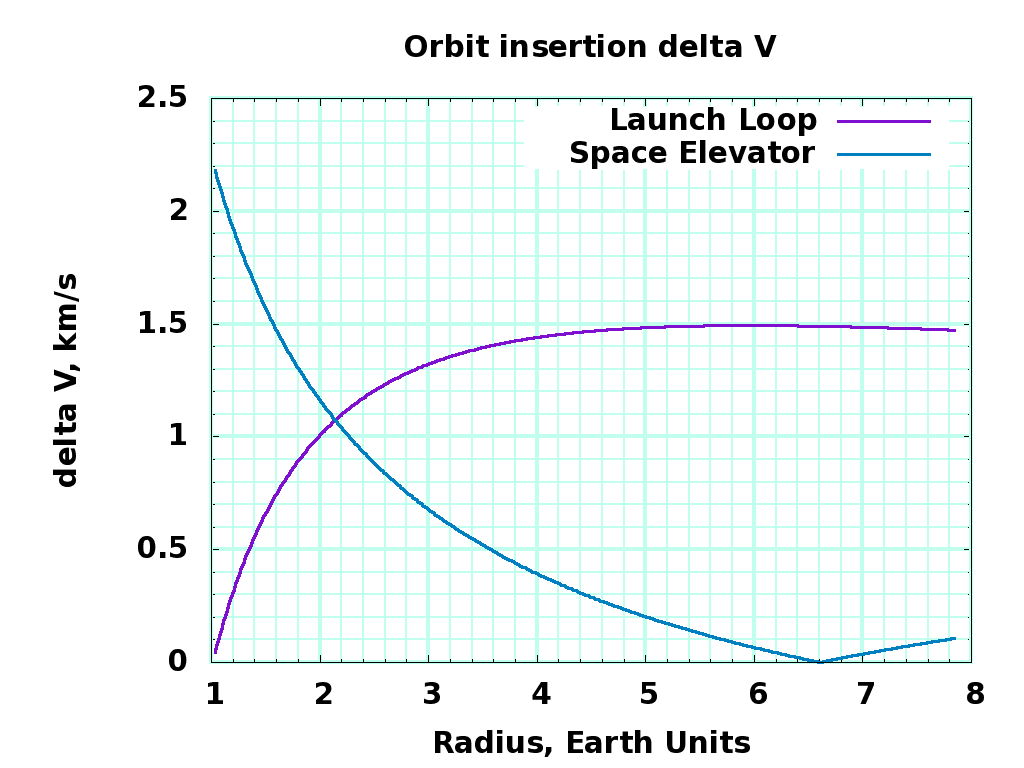
Delta V Comparison

Launch Loop payloads need less \Delta V up to 2 R_e radius ( 1 R_e altitude ). The space elevator wins above 2.5 R_e radius.

source code . . . gnuplot control file

Interestingly, the \Delta V 's at 2 R_e are 13% of the earth launch velocity to that altitude, about 1100 m/s, and are in opposite directions for the two systems. Conceivably, a tether system strung vertically between two counterweights could make an orbiting "landing pad" at 2 R_e , with payloads travelling down from the space elevator slowing down on this tether, and payloads from the launch loop speeding up on it. The two systems working in tandem may both supply mass to this station, with little or no rocket reaction mass needed.

---

From Southern Latitude Launch Loop with a

Plane Change to Equatorial

---

The first launch loops will be located 5° to 10° south latitude, in the southeastern Pacific ocean, to avoid December weather and winds associated with the intertropical convergence zone. Heavier launch loops will be proportionally less affected by wind, and may be located farther north or west in the Pacific, and in the Indian and Atlantic oceans. In the beginning, even the smallest launch loops will be vastly larger than market demand, so they should be located in the region with the gentlest weather, so that weather-related launch scrubs are minimized.

A launch loop located at 10°S will launch into a similarly inclined orbit.

The launch loop can (but won't) be arranged to follow a great circle path, starting parallel to the latitude line, then curving northwards to stay under the track of an orbit. While this keeps the gravity vector aligned with the inertial vector of the loop rotor, it does not change the inclination of the launched objects.

Instead, a launch loop will be constrained to the same latitude line, and launch into the same inclination, because the loop defines the perigee of the resulting transfer orbit.

If the destination orbit is a circular orbit in the equatorial plane, then after release, two velocity change impulses are needed:

• From elliptical transfer orbit to circular orbit (at apogee)
• From inclined orbit to equatorial orbit (at the semilatus rectum, which is where the orbit crosses the equator)

In what order should these impulses occur?

The velocity at the semilatus rectum of the transfer orbit ( \theta = 90° ) is v = v_0 = \sqrt{ 2 \mu / ( r_a + r_p ) } , which is always greater than the velocity in the destination circular orbit v = \sqrt{ \mu / r_p } . For an inclination change of \alpha , the velocity impulse is equal to 2 v \sin( \alpha / 2 ) . Minimizing the orbital velocity at the plane crossing minimizes the velocity impulse for inclination change.

So, the inclination change should happen after orbit circularization.

A diagram is needed here

As the transfer orbit is almost always north or south of the equatorial plane, the chance of a collision is minimized. The crossings of the equatorial plane will have the same orbital period as circular orbits with that radius from Earth, so they will be relatively easy to synchronize with assets in those orbits. This is especially important if a slow, high-ISP solar-electric engine is used, since the solar panels have a large collision cross section. The orbit can be raised slowly (but fuel efficiently!), always in synchonization with equatorial orbits. When the orbit is circular (but still inclined!) it will cross the plane at the same angle as its destination orbital slot, and the inclination can be slowly reduced with the same slow, high-ISP engine.

If a lower-ISP, high thrust chemical combustion rocket engine is used, then two "instantaneous" impulses can be used, first at apogee to circularize, the second a quarter orbit later to correct inclination. The same relative efficiencies apply, and collision risk is minimized further by the lower time spent between launch and destination. Combustion rockets will deliver "perishable" cargos (like cryogenic liquids, or astronauts, or time-sensitive packages) less fuel-efficiently but much more quickly.

The exhaust from a circularization burn will be emitted retrograde, opposite to the direction of orbital motion; if this is a chemical rocket with moderate ISP, the atoms will probably fall to Earth. The exhaust molecules from the plane-change burn will be emitted to the north or south, and will probably remain in orbit. The long-term fate of these tonnes of molecules is uncertain; if the destination orbit is in the van Allen belt, the molecules will slowly collide with the trapped particles, perhaps diffusing them into the loss cone and dissipating the belts, or neutralizing them, or ???