Vehicle Nose Heating
"I would rather be vaguely right than exactly wrong." - Carveth Read, 1896, in "Logic: Inductive and Deductive"
I'm still learning about the heating of nosecones. What follows probably has many errors, and would benefit from professional review and correction.
Launch loops will supply very inexpensive kinetic energy to one-time-use cargo vehicles, launching them horizontally along the axis of the loop. Drag will not reduce that kinetic energy very much, but it could overheat the nose. We can expect the upper atmosphere at the equator to be very turbulent and variable. That will add some uncertainty to the exit velocity, requiring exit velocity adjustments. Since the vehicle will be inexpensive and almost entirely passive, we will probably use laser-ablative thrust of ablative panels attached to the sides of the vehicle to make sub- m/s adjustments; smaller adjustments permit smaller, cheaper, power-thrifty lasers.
Traditional launch rockets normally rise vertically, and do most of their acceleration in space vacuum, at least 100 km above the surface. However, the heat resistant nose cones needed to exit the atmosphere "horizontally", from 80 km loop altitude to space vacuum, could be more expensive. What is needed to protect the vehicle nose from thin but extremely energetic gas?
Symbol Table |
|||
Pr |
Prandtl number |
|
|
Re |
Reynolds number |
|
|
H/s |
Power/area |
W/m² (watt/m², kg/s³ ) |
0.0685218 slug / s³ |
ρ |
air density |
kg/m³ |
1.94032e-3 slugs / ft³ |
m |
mass |
kg |
0.0685218 slug |
σ |
nosecap radius |
m (meter) |
3.28084 ft |
V, u |
freestream velocity |
m/s |
3.28084 ft/s |
T |
Absolute temperature |
K (kelvin) |
1.8 °R (rankine) |
Q |
Heat transferred |
J (joule) |
0.737562 ft-lb |
μ |
viscosity |
kg/m/s |
0.0208854 slugs/ft/s |
subscripts |
|||
r |
recovery conditions |
||
s |
stagnation conditions |
||
w |
wall conditions |
||
According to the standard atmosphere model, the atmosphere at 80 km is 1.8458e-5 kg/m³, 1.5e-5 as dense as that at the surface (I expect it to be denser at the equator than at the 45.5425 degree latitude of the standard model). For a 10 km/s exit, the total enthalpy (thermal and chemical power) of the free stream flow approaching the nose cone is ½ ρ V³ = 9.23 MW/m². That is a lot of heat; fortunately, most of it remains in the gas, not on the nose.
Allen and Eggers
A seminal paper in space history is "A Study of the Motion and Aerodynamic Heating of Missiles Entering the Earth's Atmosphere at High Supersonic Speeds" by H. Julian Allen and A. J. Eggers, Jr. The revised October 1957 version is NACA (National Advisory Committee for Aeronautics) Technical Note 4047, available as 19930084817.pdf from NTRS, the NASA Technical Reports Server.
This paper teaches that a hypersonic reentry body nose should be rounded, not pointy. A pointed nose will endure higher heating at the point, and cannot conduct heat fast enough to the body behind, so it will burn away. The thermal stresses may shatter the nose cone. A rounded nose will move the shock wave farther in front of the vehicle, and deflecting more of the entry heat into the air, and less to the stagnation point (the center of a symmetric flow) on the nose itself.
The Allen/Eggers paper concerns warhead entry; the idea is to deliver an intact and functioning warhead near the surface without damaging it. Launch loop, launching into the equatorial plane, won't overfly most strategic cities, so hopefully billions of people will not be threatened by it. On the other hand, more of those billions can travel to space if nosecones are cheap and effective.
PICA - Phenolic Impregnated Carbon Ablator - is the gold standard for reentry heat shields, but those heat shields cost millions.
Heppenheimer's Facing the Heat Barrier: A History of Hypersonics NASA sp4232 offers a fascinating history of nosecone development. Page 50 offers this amusing sentence:
Indeed, Kantrowitz recalls Von Braun suggesting that it was possible to build a nose cone of lightweight balsa soaked in water and frozen. In Kantrowitz’s words, “That might be a very reasonable ablator.”
Water evaporates too easily, and balsa is expensive and rare. A possible alternative is chemically modified, porous "nanowood" infused with polydimethylsiloxane ... silly putty. Designed properly, they could be manufactured by South American furniture factories.
Launch Loop cargo exit nosecones need not reenter, just survive an outbound trip through the thin upper atmosphere from the perigee of a high apogee Kepler orbit.
Back to Allen/Eggers ...
Stagnation point heating is described by equation 44, unfortunately in foot pound second units:
{ \Large { { d H_s } \over { d t } } } ~ = { 6.8e-6 } ~~ { \Large \sqrt{ \rho \over \sigma } } ~ V^3
Let's try scaling that to meters kilograms seconds:
slugs/s^3 = 6.8e-6 (units?) ~ { \Large \sqrt{ slugs/ft^3 \over ft } } ~ { ft^3 / s^3 }
\sqrt{ slugs } / ft = 6.8e-6 (units?)
So, the units of the multiplier are \sqrt{ slugs } / ft . To convert the multiplier to mks, multiply 6.8e-6 by 3.28084 / \sqrt{ 0.0685218 } to get 8.5e-5 \sqrt{ kg } / m .
The metric version of equation Allen/Eggers 44 is thus:
Eq 44_m: ~~~ { \Large { { d H_s } \over { d t } } } ~ = { 8.5e-5 ~( \sqrt{ kg } / m ) } ~ { \Large \sqrt{ \rho \over \sigma } } ~ V^3
For a 20 cm radius nose, V = 10 km/s, \rho = 1.8458e-5 kg/m³ and \sigma = 0.2m, the stagnation point heating rate is approximately 820 KW/m² .
For a 50 cm radius nose, the heating rate drops to 520 KW/m².
This is pessimistically high heating; at these high velocities, real gas will dissociate and partly ionize, absorbing much of the stream entropy at a lower temperature. As the surface of the nose cone heats, it will absorb less entropy from the stream. On the other hand, some of the atomic oxygen and ions will recombine at the nose, releasing energy. So, treat these numbers as a conservative worst case. Both numbers are a LOT better than the total free stream enthalpy 9200 KW/m².
The Rest of the Nose Cone
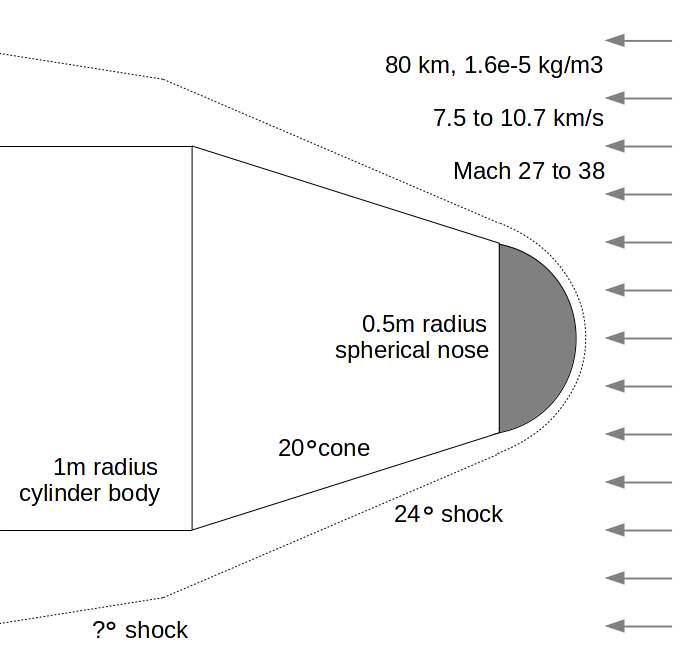
Assuming a hemispherical nose cap in front of a 1m radius nosecone, we will assume the heat absorbed by the entire nose cap diminishes as the cosine of the angle of the nose, until it merges with the conical body of the nose. For the overall drag, we will use a modified version of Newton drag, with shock effects expanding the stream deflection angle by 20%. |
|
I don't know how the heating varies with the slope of the spherical nose; it may decrease as sin(θ), the way the projected Newton drag does (The force normal to the surface is sin²(θ) ).
Kinetic Energy Lost During Exit
The exit vehicle accelerates enclosed in the launch sled, which has its own nose cone, and may (hypothetically) use a track-powered longitudinal electric arc to expand the gas in front of the launch sled nose. After vehicle release, the sled continues to accelerate. All sleds follow the same time/velocity "schedule", one after the other, so even empty sleds that released vehicles to low orbit will follow the same velocity/distance program as sleds that release to higher orbit.
The released vehicle still has some thin atmosphere to plow through, in its drag-modified Kepler orbit to the destination perigee. It will lose some velocity from thin atmospheric drag. Let's use the Newton approximation to the shock wave to estimate that drag.
Enthalpy will be very high, and real gas effects will result in a smaller specific heat ratio (\gamma) and a somewhat smaller shock angle than the 20% angle increase associated with the "classical" \gamma=1.4, the ratio of specific heats. But there will also be some extra body "skin" drag, which I don't know how to calculate. Since energy dissipated by nose heating, skin drag, and shocked atmosphere is supplied by vehicle kinetic energy (slowing it down), lets estimate the total shock force for \gamma=1.4, and a shock angle of 24° around the cone, and assume that pessimistic assumption makes up for body drag.
Assume the radius of the shock around the hemispherical nose cap is R = 0.6 meters, 20% larger than a 0.5 meter physical nose cap. The hemispherical shock is not a complete half-sphere; it merges with the cone shock at θm = 90-24° = 66° from the centerline.
Consider a "hoop" element of spherical shock between angle θ and θ+dθ from the centerline. It is inclined to the stream by θ, and the area of that hoop element is 2π R² cos(θ) dθ. The forward projected area of that hoop element is diminished by cos(θ). The Newton drag per associated with that tilted hoop element is 2 ρ V³ sin(θ) per m². So the total drag on the nosecap is
Nosecap drag = \int_0^{θ_m} { ρ V³ \sin( θ ) ~ 2 π {R_n}^2 \cos( θ ) dθ } ~~ = ~~ π ρ V³ ~ R_n^2 \sin( θ_m )^2
The rest of the cone is easy - the projected area of the cone is an annulus hoop with outer radius of R_o of (1 meter as illustrated above) and an inner radius of R_n \cos( θ_m ) , so the area is π ( {R_o}^2 ~-~ ( ~ R_n \cos( θ_m ) ~ ) ^2 ~ ) .
The cone drag is 2 V³ \sin( θ_m ) multiplied by that area, or
π ρ V³ \sin( θ_m ) ~ ( {R_o}^2 ~-~ ( ~ R_n \cos( θ_m ) ~ ) ^2 ~ )
Added together, the resulting total vehicle drag is:
π ρ V³ \sin( θ_m ) ~ ( {R_o}^2 ~+~ R_n^2 ( \sin(θ_m)^2 - \cos(θ_m)^2 )
simplified with ( cos^2 = 1 - sin^2 ) :
Total vehicle drag = |
π ρ V³ \sin( θ_m ) ~ ( {R_o}^2 ~+~ R_n^2 ( 2 * \sin(θ_m)^2 - 1 ) |
Define scaling factor SF = 2 π \sin( θ_m ) ~ ( {R_o}^2 ~+~ R_n^2 ( 2 * \sin(θ_m)^2 - 1 )
And Enthalpy H = 0.5 ρ V^3 such that Total vehicle drag H * SF
Deceleration is drag / M V .
Examples
Sound speed |
c |
282.54 |
m/s |
Spacecraft mass |
M |
5000 |
kg |
Spacecraft diameter |
R_o |
1 |
m |
Nose Radius |
R_n |
0.5 |
m |
Specific Heat Ratio |
\gamma |
1.05 |
real gas |
Shock angle |
θ_m |
21 |
degrees |
sin( Cone angle ) |
|
0.358368 |
|
scaling factor |
SF |
1.833 |
m^2 |
Mission |
400 km LEO |
M288 |
GEO |
HEEO-1d |
HEEO-7d |
escape |
Apogee km |
6778 |
12789 |
42164 |
75950 |
300205 |
\inf |
Launch km |
6454 |
6457.8 |
6458 |
6458 |
6458 |
6458 |
Angle tan |
0.0252 |
0.0012 |
0.000 |
0.000 |
0.000 |
0.000 |
Vtotal km/s |
7.574 |
9.789 |
9.875 |
10.195 |
10.522 |
10.640 |
Mach |
26.8 |
34.6 |
35.0 |
36.1 |
37.2 |
37.7 |
Radial Shock Mach |
10.9 |
14.1 |
14.3 |
14.7 |
15.1 |
15.3 |
Kinetic energy MJ |
143400 |
239600 |
243800 |
259900 |
276800 |
283000 |
Vx km/s |
8.042 |
9.606 |
10.346 |
10.666 |
10.993 |
11.111 |
Vy km/s |
0.191 |
0.011 |
0.000 |
0.000 |
0.000 |
0.000 |
H MW/m² |
7.45 |
7.25 |
8.89 |
9.78 |
10.75 |
11.12 |
Drag MW |
14.5 |
13.3 |
16.3 |
17.9 |
19.7 |
26.5 |
deceleration m/s² |
0.38 |
0.27 |
0.33 |
0.35 |
0.38 |
0.39 |
- note 1: Vx includes Earth rotation velocity near 80km altitude, ≈ 0.471 km/s.
- note 2: The vehicle spends less than 30 seconds climbing out of the atmosphere.
- The "centrifugal acceleration" exceeds gravity, and approaches -1 gee near escape v
- The vehicle climbs out slowest on a trajectory to LEO, fastest to high orbits
- note 3: For LEO, and orbital destinations up to "M288" (a 288 minute earth-rotation-relative orbit), the launch path is slightly curved, to impart some initial vertical velocity, and reduce climbout time. That lowers the release altitude, and increases drag for the first few seconds of the climbout.
- note 4: High orbit apogee radius is very sensitive to tiny changes in exit velocity
A future version of this document will include "integrated air column" estimates for climbout, to estimate total velocity loss. Launch acceleration is 30m/s², so an extra second or two of delay before release will compensate for the average loss.
Thick Heatshield Weather: Seasonal changes, day/night cycle, solar activity, vehicle and payload differences, and thermospheric turbulence will add variance to the loss. Even with perfect modelling, post exit and midcourse velocity tweaks will be needed for high precision vehicle delivery to the destination. When the upper air is especially dense, thicker heatshields may be required for the exit vehicles.
Historic Space Vehicle Mass and Radius
The page above assumes a 5 tonne, 2 meter diameter vehicle. How does this compare to other missions?
Spacecraft |
Diameter |
Mass |
notes |
Mercury capsule |
1.80m (base) |
1400 kg |
|
Gemini capsule |
2.32m (base) |
3851 kg |
including retro and equipment module, adapter 3.05m |
Dragon capsule |
3.66m (base) |
12055 kg |
including trunk |
Apollo capsule |
3.90m (base) |
28800 kg |
Block II, including service module |
Skylab |
6.61m |
77111 kg |
|
Mir (Kvant module) |
4.15m |
20400 kg |
multiple launches, 7 modules |
Apollo Lunar module |
4.22m (w/o legs) |
16400 kg |
launch fairing probably larger |
Telstar 19v comsat |
4m fairing |
7076 mg |
|
KH-11 |
3m? |
19600 kg |
|
Hubble Space Telescope |
4.2m |
11100 kg |
|
Tiangong-2 |
3.35m |
8600 kg |
Eventually, mission descriptions will get their own webpage.