Generator Model
The Launch Loop electrically extracts power from the laminated iron and aluminum winding rotor through aluminum stator windings and delivers it to the Halbach arrays on the magnet sled. The current design has six centimeter-scale stator slots with laminated iron on both sides; this approximates an induction generator 15 centimeters wide.
Accurate modelling of the induction generator requires 3D finite element modelling and experience with error avoidance - simulation tools are garbage in, garbage out. Given the ultra-high rotor speeds, my guess is that slip will be very low, and the stator field will travel forwards at speeds very close to the 12.5 km/s rotor speed.
Induction generators require reactive power to establish the field. The customary approach requires capacitors to store field energy, but 2000 km of capacitors capable of briefly moving megawatts per winding is expensive and heavy. I will assume we can supply the VAR (volt-amp-reactive) power from the Halbach arrays on the vehicle sled. For this discussion, assume a 50 meter long Halbach array with 10 centimeter pole-pair pitch, or 500 wavelengths. The first and last 5 meters of the sled will be an exciter, feeding kinetic energy from the vehicle to the rotor to establish a magnetic field in rotor and the stator plenums. The last five meters will extract the field energy back out, and into the vehicle sled. The exciter windings will drag on the sled, the extractor windings will pull it, helping maintain the sled in tension.
How much acceleration power?
The design assumes around 200 KN pushing the vehicle and sled at 30 m/s². For a vehicle accelerating to 10600 m/s (near escape velocity, plus exit drag), the drive power will increase from around zero at the start to 2.12 GW, approximately 1800 kilometers eastwards down the track. The "jerk" or change in acceleration might be 10 m/s³, occuring over 3 seconds, at beginning and end.
See FirstTrack for details of initial track acceleration. That results in a vehicle/sled moving at 1000 m/s and 17 km along the track at T=38 seconds.
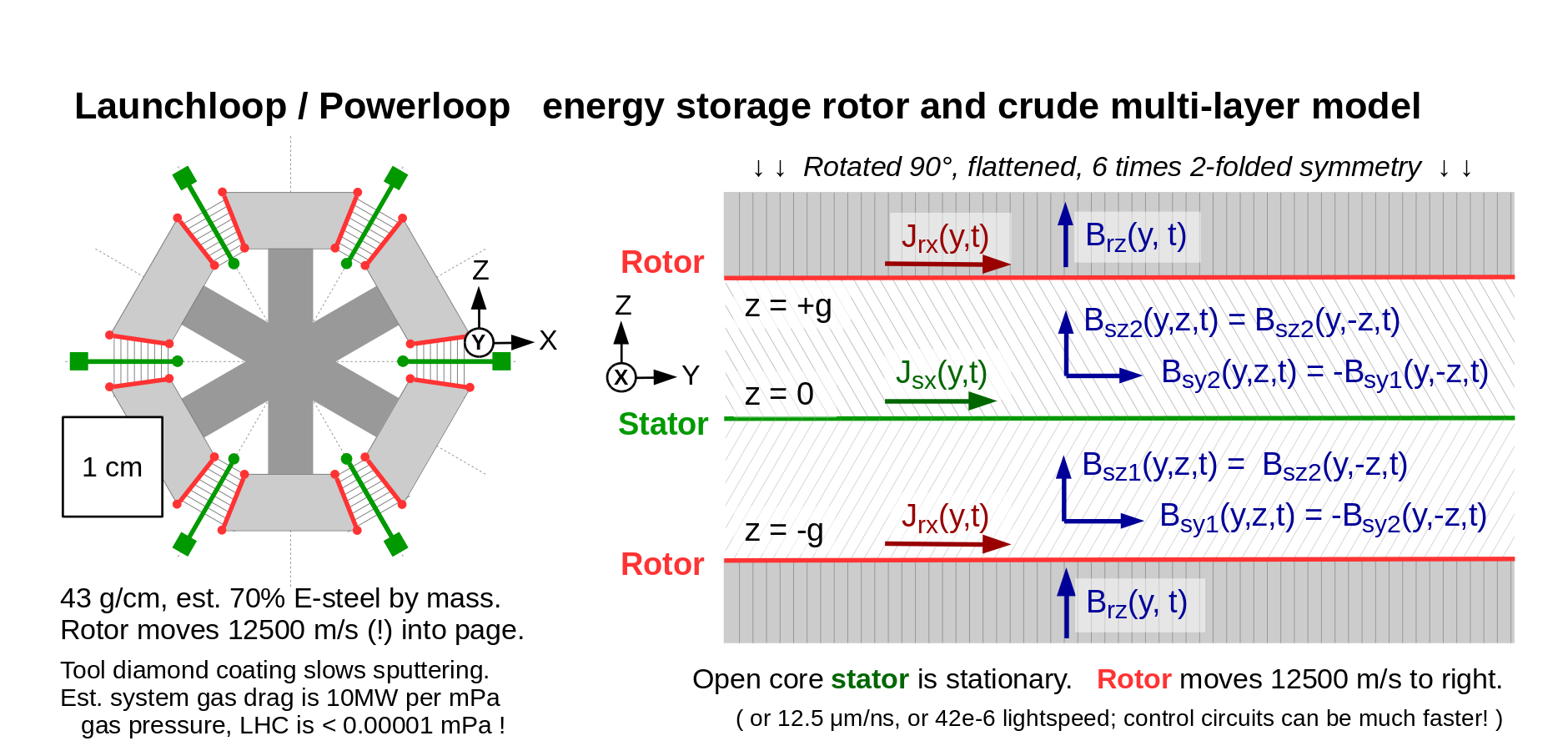
Multi Layer Model
For a traditional rotary induction motor, the multilayer model approximates field behavior. Electromagnetic Power Conversion by Levi and Panzer (second edition, Dover, 1974) contains appendix B (pages 465 to 469), Determination of the Magnetic Field Associated with a Sinusoidal Current Sheet on the Surface of a Rectilinear Air Gap.
I will modify and simplify this slightly. The model is static; I need to add time dependence.
grumble: The motor literature uses \large \tau for a half wavelength, rather than the customary \large \lambda for a full wavelength. I will reluctantly do so here. \large \tau is also used for circuit time constant. Some suggest \large \tau as a replacement for 2 \large \pi . Also, { \large \tau } = {\small { 1 / \sqrt{ 1 - ( v^2 / c^2 ) } } } is the length scaling multiplier in special relativity; Laithwaite points out that magnetic effects can be modelled as relativistic Coulomb effects, hence special relativity is worth consideration. Ah well; perhaps a large and extensible set of mathematical emoji is the best long-term answer.
The model is an infinite sheet of conductor in the x-y plane, with infinitely permeable material below z = 0 and above the gap z = g .
The planar current density K (measured in amps per meter in the Y direction) is K = K_m \cos( ~ { \large { \pi \over \tau } } ~ x ~ ) . After some clever math, the Levi/Panzer derivation produces a magnetic potential:
A_y = { \Large { { \tau \mu_0 K_m } \over \pi } } ~ { \Large { { ~ \cos( ~ { \LARGE { \pi \over \tau } } ~ x ~ ) } \over { \sinh( ~ { \LARGE { \pi \over \tau } } ~ g ~ ) } } } ~ \cosh( ~ { \Large { \pi \over \tau } } ~ ( g - z ) ~ )
and magnetic fields:
B_x = ~ \mu_0 K_m ~ { \Large { { ~ \cos( ~ { \LARGE { \pi \over \tau } } ~ x ~ ) } \over { \Large \sinh( ~ { \LARGE { \pi \over \tau } } ~ g ~ ) } } } ~ \sinh( ~ { \Large { \pi \over \tau } } ~ ( g - z ) ~ ) ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ B_z = - \mu_0 K_m ~ { \Large { { ~\sin( ~ { \LARGE { \pi \over \tau } ~ x ~ ) } \over { \Large \sinh( ~ { \LARGE { \pi \over \tau } } ~ g ~ ) } } } } ~ \cosh( ~ { \Large { \pi \over \tau } } ~ ( g - z ) ~ )
The multilayer model for a six-lobed launch loop rotor can be absurdly simple. The flux wraps around the rotor circumferentially, passing through six open-core stators and six laminated iron cores with a radial rotor "squirrel cage" on each face. Presuming infinite rotor permeability, and given a propagating field in the stator current sheet, we need only consider the current in the rotor current sheet, and the propagating magnetic field in the vacuum gap between them.