Lowering the West Incline

With a New Track Design

Lowering the West End of the Track

Most of the acceleration track of the launch loop should be at 80 kilometers altitude, to avoid most atmospheric drag. However, near the start of acceleration, the vehicle is moving relatively slowly, and can tolerate higher air density. This is an opportunity to lower west station, permitting a shorter west incline, shorter stabilization cables, and a heavier incline. This detail is not essential to the launch loop, but it will save money and improve operations considerably.

The velocity along the track is V^2 ~ = ~ 2 a L . The drag is proportional to density and velocity squared, so for constant drag, the density can increase inversely proportional to track distance L+0 . The scale height Z_S varies between 50km and 80km geometric altitude, but averages 7200 meters. So the height is Z ~ = ~ Z_0 + Z_S \ln { L / L0 } , until we get so close to the west station and the west incline that the angle becomes limited.

The slope of the track is d Z / d L ~ = ~ Z_S / L . The curvature of the track is d^2 Z / d L^2 ~ = ~ - Z_S / L^2

Given a total track length of 2000 km, height versus track length might vary as:

That last entry is problematic - the incline starts at 20 degrees, and curves downwards, so the angle at west station is quite a bit less than 20 degrees. So the curve of the launch track must stop increasing somewhere above 50 km altitude. This is a "flat earth" calculation. The earth's curvature is -1 / R_E , or 1.57E-4 km^-1, so significant extra weight and cable tension is needed to curve the track and rotor as it approaches west station. Lets stop dropping the track quite so steeply at 150 kilometers out, limiting the curvature to 3.2E-4 km^-1. This puts the east end of West station is about 50.6 km high. This also means the first 150 km of track can mass 3 * ( ( 3.2/1.57 + 1 ) * ( 14/7.67 )^2 - 1 ) = 30 kg/m rather than 7 kg/m .

At 3 gees, the payload will spend about 100 seconds accelerating over this 150 km section. Up to 70 seconds after launch, this is a good place to abort and return a payload to west station if necessary. Since the track is sloping downwards, plain old gravity can return an aborted payload in about 15 minutes, while a 0.5 gee acceleration can return it in about 6 minutes.

We will hopefully detect most flaws within 5 seconds of acceleration start. At 3 gees, that will put the vehicle only 375 meters up the track, moving at 150 meters per second. If the vehicle brakes to a stop at 10 m/s², it will continue another 1125 meters to 1500 meters. Gravity will bring the vehicle back to the starting point in 40 seconds, perhaps shunted to another track for debug, passenger exit, etc.

The extra weight of the track can support an abort braking system, perhaps even some kind of semi-passive "velocity transformer" coil system to accelerate the payload with less drag on the rotor, and more pull on the stress-relieved track. Wild hand-waving here!

The downwards curvature adds outwards centrifugal force, v^2 z'' , tending to lift the vehicle. Let's compute the vertical acceleration, including gravity (average 9.6m/s² ) and the curvature of the earth ( -1.55E-4 km^-1 ):

approximate calculations

The upwards acceleration gradually increases until it is lifting passengers out of their seats (they are strapped in, though). The vertical acceleration ceases when the vehicle releases from the track at east station, about 2 minutes later.

The air density at 80km is 1.85e-5 kg/m³. Assuming a 5 meter square cross section, a drag coefficient of 0.2, and a mass of 5000 kg, after the vehicle leaves the acceleration track it decelerates at 0.22 m/s². This reduces gradually over the next minute, as the vehicle climbs out of the atmosphere, and passengers will experience zero gee. While the air drag reduces, as the vehicle climbs it gradually exchanges kinetic energy for potential energy, and continues to slow down.

Gradual reductions in acceleration and ramp curvature approaching, and through, east station can adjust the changes felt by passengers. The region around east station is also where small amounts of lateral \Delta V can be added to adjust inclination slightly from the equatorial plane.

Effect on West Station and the West Incline

Because west station is lower, the west incline joins it at a steeper angle. The stabilization cables are not as tall, meaning they can be lighter for the same horizontal relief force. However, there is a much larger horizontal force from the steeper angle of the station, and combined with the slope hanging cables this results in much more vertical cable force. To compensate for this, assume that the descending cable runs at a lower slope, angling more directly towards west station, a rise of 30 km in 2000 km, or an angle of 0.85 degrees .

The cable slope is given by \sqrt{ e^{ {2(z+{z_0})}/{Z_S}} - 1 } / \cos{ \theta_{side} } . Assume \theta_{side} = 45 \deg , z_0 ~ = 20 km, and Z_S ~ = 80 km .

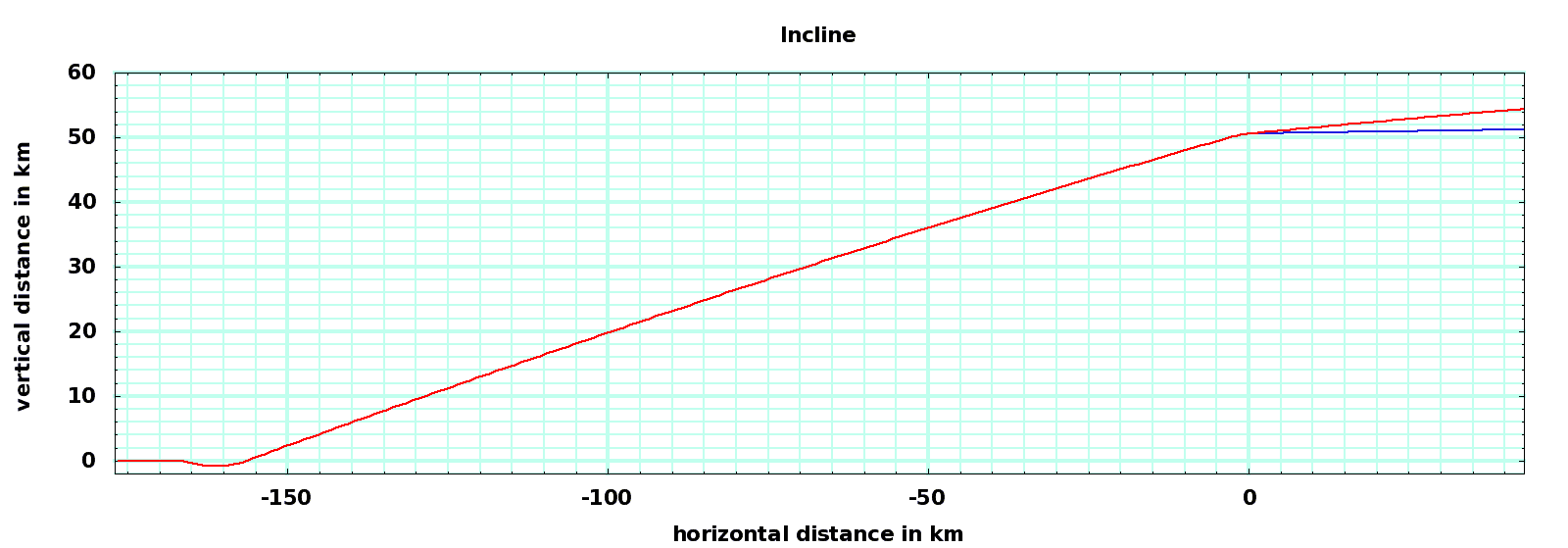
Here is a plot of the west incline (red is launch path, blue is reverse path):

The source and the gnuplot control file.

WORK IN PROGRESS, MORE LATER