Construction1

This will be merged with ConstructionOrbits real soon now.

---

captur10.w1 --- added to Construction1

This analysis ignores second-order effects like lunar/solar/Jupiter tides, apsidal precession from Earth oblateness, light pressure, and outgassing, which will add seconds and many meters of perturbations to the precision calculations needed to deliver a vehicle to a rendezvous at an exact position and time. With years of experience and calibration, the launch loop will evolve into a precision instrument for millimeter-accurate delivery of vehicles to destinations.

However, the following calculations will be better than 0.1% accurate, useful for estimating delivery rates and infrastructure requirements. It is better to be roughly right than exactly wrong.

---

Construction orbit, Act 1

Begin with a construction orbit, with a period of one sidereal day. There are 366.2422 sidereal days per 365.2422 solar days of 86400 seconds, so the construction orbit period is ~~~~ T_c = 86164.0905 seconds

The angular frequency of the construction orbit is ~~~~ \omega_c = 2 \pi / T_c = 7.2921158e-5 radians/second

The Earth's standard gravitational constant is μ = 398600.4418 km³/s². The semimajor axis of a one sidereal day orbit is ~~~ a_c = ( \mu ( T_c / 2\pi )^2 )^{1/3} = 42164.1696 km

The construction orbit perigee should be above the LEO space debris, collision, and litigation belt. Arbitrarily choose a perigee radius 2000 km above Earth equatorial radius: ~~ r_{cp} = 2000 + 6378 km = 8378 km

The construction orbit apogee is twice the semimajor axis on the opposite side of the Earth from the (negative) perigee, so the apogee radius is ~~~ r_{ca} = 2 a_c - r_{cp} = 2 * 42164.1696 - 8378 = 75950.3392 km

Deviating from "standard" treatments, we will choose our reference angle, time, and other orbit parameters in relation to apogee, not the usual perigee. The eccentricity of this orbit is negative: ~~~ e_c = r_{cp} / a_c - 1 = 8378.0 / 42164.1696 - 1.0 = -0.8013005 (no units)

The construction orbit perigee occurs one half a period before time zero: T_{cp} = 0.5 T_c = -43082.0452 seconds

The construction orbit perigee velocity is:

v_{cp} = \sqrt{ ( \mu / a_c ) ( r_{ca} / r_{cp} ) } = \sqrt{ ( { \small 398600.4418 } / { \small 42164.1696 } ) \times ( { \small 75950.3392 } / \small { 8378 } ) ~ ~ } = 9.25746 km/s

The construction orbit apogee velocity is:

v_{ca} = \sqrt{ ( \mu / a_c ) ( r_{cp} / r_{ca} ) } = \sqrt{ ( { \small 398600.4418 } / { \small 42164.1696 } ) \times ( { \small 8378} / \small { 75950.3392 } ) ~ ~ } = 1.02118 km/s

There can be thousands of different one day construction orbits with the same apogee, perigee, and period, but arriving at apogee at different times throughout the sidereal day. The constellation will resemble the petals of a flower; while the orbital tracks intersect, two different stations associated with the same launch loop will not pass through the same intersection simultaneously.

Unless the entire construction station is well shielded, the crew must be confined to a shielded core surrounded by lots of hydrogen (food, waste, water, fuel) that can attenuate the dose. If the orbit passes through the radiation belt only once per day, this can be the rigidly scheduled sleeping period, every 23 hours and 56 minutes.

Astronauts are superbly competent people, so they can get their day's work done 4 minutes faster than the rest of us.

If the construction orbit perigee is "sidereal midnight", apogee is "sidereal noon". As we will see, "noon" is when passengers and supplies arrive from Earth, and when passengers and products return for reentry. Launch and entry orbits will have smaller perigees, a smaller semimajor axis, and thus somewhat shorter orbit times than the construction orbit.

---

Multiple Day Construction Orbits

The period of the construction orbit need not be one sidereal day, but it should be an integer ratio fraction of a sidereal day.

For example, a 5/3 sidereal day orbit will have a larger semimajor axis than the one day orbit, proportional to the 2/3 power of the period, or 59271 km. The perigee might still be 8378 km, yielding a 110164 km apogee. Since the launch loop rotates around the Earth once per sidereal day, the apogee of this construction orbit is accessable only once every three orbits, or every five sidereal days. Such orbits are interesting, but not as practical as simple integer ratios. A 5 sidereal day orbit may actually be more useful - one third of the passes through the van Allen belt, and a higher perigee velocity for the start (and end) of interplanetary missions.

Another example is a 1/2 sidereal day orbit, with a semimajor axis of 26562 km. If perigee is 8378 km as before, apogee is 44745.524 km. The launch velocity is lower, but the capture velocity is higher. This orbit can intersect with loop launches only once per day, because the launch loop is halfway around the world at the other hypothetical launch time. This also accentuates a problem shared by all orbits with "low" perigees; they pass through the van Allen belt during descent and ascent more often and more slowly than higher orbits, so more crew time spent in the shielded core. Indeed, the peak of the outer belt is at 5 Re, about 32000 km, Such orbits are more practical for crew-less automated stations; if the crew cannot work outside shielding, then telepresence is a more practical way to work there.

High integer multiple orbits: 2, 3, 4 etc. sidereal days, are also useful, but orbits with apogees near lunar radius may be (WAG) more sensitive to lunar gravitational perturbations. The Moon's semimajor axis is 384399 km, though lunar perigee and apogee vary because of solar tidal forces. Both lunar and solar "tides" will perturb construction orbits. and launches to them.

So, the most practical construction orbits are likely to be 1, 2, 3 ... 6 sidereal days. For the rest of this discussion, we will focus on launches to the 1 sidereal day construction orbit; this may offer the best compromise between rapid assembly and a higher v_{\infty} .

We will continue the construction orbit description later, after considering how to get there from a launch loop.

---

Prime orbit, Act 1

From here on out, we will round distance to the nearest kilometer and the time to the nearest second.

The prime orbit is an unmodified launch orbit, with the same apogee time ( 0.0 seconds ) and the same apogee radius as the one sidereal day construction orbit: r_{pa} = 75950 km.

The launch orbit perigee is the altitude of the launch loop (assumed to be 80 km) added to the radius of the Earth: r_{pp} = 6378 + 80 km = 6458 km. The prime orbit semimajor axis is: a_p = 0.5 * ( 6458 + 75950 ) = 42104 km The period of the prime orbit is: T_p = 2 \pi \sqrt{ a_p / \mu } = 85980 seconds.

The trajectory time is half the full orbit, or 42990 seconds, or 11 hours 56 minutes and 30 seconds. Prime orbit perigee time is before zero time, or t_{pp} = -42990 seconds.

That is 92 seconds after the construction orbit passed overhead. The prime orbit perigee velocity is 10551 m/s. 471 m/s is provided by earth rotation velocity, and an additional 30 m/s WAG) is needed for air friction during exit. The estimate loop-related launch velocity is 10110 m/s, or 337 seconds of acceleration at 30 m/s . The acceleration run begins 337-92 = 245 seconds before construction orbit perigee, and 1700 km to the west of the release point.

Near apogee, the construction orbit station is moving at 9.257 km/s, so it will be aproximately 2200 km west of the release point, and 2000 km overhead, or 500 km west of launch loop west station, at an elevation of atan( 500/2000 ) or 14 degrees from zenith. There will be plenty of warning time to abort the launch from the loop, though that can lead to logistic complications for fast assembly.

---

Prime Launch

The launch loop launch track can be at altitudes between 70 km and 120 km. The drag and heating at 120 km is very low, but that means space debris deorbits more slowly, greatly increasing the debris flux and impact hazard. At 70 km loop altitude, the drag is 4.7x higher and the temperature (in Kelvins) is 11% higher, so the vehicle drag and heating is 5x higher than the slightly higher 80 km, making the vehicle nose shroud heavier and more expensive. We will choose 80 km for this exercise.

The earth rotates one sidereal day in 86141.0905 seconds. At 6458 km radius, that is a rotation velocity of ( 2 π 6458000 / 86141.0905 ) = 471 m/s . The launch velocity is the apogee velocity minus the rotation velocity. More precisely, we must add a little bit of extra launch velocity to counteract drag leaving the atmosphere; the amount of drag loss will depend on vehicle aerodynamics and atmospheric conditions, but will probably be less than 30 m/s. Production launches will use realtime atmospheric measurements and exact vehicle measurements to model this effect, resulting in exact trajectories trimmed to millimeters per second.

Prime launch delivers vehicles to the apogee of the construction orbit from the launch site at 6458 km radius (80 km altitude). Before a more versatile capture system is assembled, this is the easiest way to get initial materials to the construction orbit station, without a plane change, once per sidereal day.

The arrival velocity is the prime orbit apogee velocity minus the 1021 m/s construction station apogee velocity. That velocity will be faster, and some onboard vehicle thrust will be needed to bring incoming vehicles up to speed. Later, we will discuss cable capture, a way to minimize vehicle cost and complexity by using construction station momentum and makeup thrust.

Orbital characteristics referenced from apogee:

A 142 m/s apogee boost is much smaller than the injection velocity for a circular orbit at 75950 km radius; indeed, it is smaller than the injection velocity into any circular orbit above 275 km altitude. This is why construction orbits are the best destinations from the launch loop.

---

Reentry after Capture/Rendezvous failure

If the vehicle fails to rendezvous with the station, it cannot quickly resynchronize for a second pass. The prime orbit period is shorter than the one day sidereal orbit, so the vehicle will arrive after another orbit 161 seconds ( 86141 - 85980 ) early. It may be best to re-enter (assuming a heat shield) and re-launch. If a low-cost cargo vehicle lacks a heat shield, let it re-enter and burn up. A 40 km altitude ( 6418 km radius) is assumed sufficient to lose enough velocity to descend, so a launch orbit abort reentry orbit will look like so:

This delta V can be accomplished with laser ablation. In addition, the vehicle should have a rocket capable of 3 m/s retrograde thrust.

A much larger retrograde thrust at can re-enter from the construction orbit, starting at apogee:

---

Prime Capture at Docking Station

Approaches to ISS involve a complicated set of manuevers that take up to 8 hours. ISS is a bag of air wrapped in aluminum foil, easily damaged by a collision. A capture station will be larger, heavier and far more robust, and approach speeds from launch orbits will be slower. An amusing alternative is an armored lower docking station suspended on stout cables below the main station, plus deployable capture lassos that grab the tailhooks of approaching vehicles. This is an incredible kludge, but it means that system propulsion can be a fixed rocket on the docking station, shared among hundreds of vehicles a year (some of them propellant tankers).

A single construction station may deploy dozens of docking stations, capturing many incoming vehicles sequentially, perhaps 100 tonnes per day. This is no job for pilots; computers will measure, simulate, and adjust positions and velocities to millimeter accuracy. There are no waves or wind in orbit, and computers and sensors are very fast. In zero gee and high vacuum, with laser interferometry, real-time computer simulation, and high precision actuators, we will learn to capture incoming vehicles faster and more accurately than a tailhook landing on a aircraft carrier.

An incoming vehicle with 200 m/s retrograde velocity (the station moves faster than a vehicle at apogee) moves only 200 micrometers in a microsecond, which is ample time to make an interferometric measurement, update a simulation model, and apply power to an actuator. With limited power, mechanical movements will be slow, but the system has performed nearly identical operations many times before; the control system will be correcting unexpected errors, not discovering de novo what to do. At the speed of light in optical fiber, a sensor reading can travel 200 meters in a microsecond. Compared to "electronics world", "mechanical rendezvous world" is very slow and predictable.

5000 kg vehicles launch from the loop with an acceleration of three+ gees, 30 m/s²; if vehicle contents remained well secured during the 12 hour zero gee trajectory, a 10 m/s² deceleration along the same vehicle axis is tolerable. That is 20 seconds of deceleration, and a 2000 meter deceleration run. One possibility for hookup is to launch the tethered deceleration probe slowly along the trajectory of the incoming vehicle direction, stop it perhaps 1200 meters away, then pulling it towards the docking station at 10 gees, accelerating to 200 m/s inwards in 2 seconds, exactly matching the incoming vehicle's velocity vector and position 1000 meters out.

This allows 5 seconds to manuever and latch onto the vehicle, while the deceleration probe tether is reeled in at the station. The vehicle whips by at 200 m/s, and the pull motor reverses in a couple of seconds, becoming a generator. The cable pulls on the generator; If the vehicle and cable mass 6000 kg, and the combination decelerates at 10 m/s². The force transmitted to the station will be 6000 kg × 10 m/s² = 60 kN. This decelerates the vehicle and cable to zero velocity 20 seconds, and adds a net 1000 kN-s momentum impulse to the station as vehicle, cable, and station match velocities.

The peak generated power is 6000×10×200 = 12 MW, dropping to zero as the vehicle slows to a stop.

---

Restoring Docking Station Momentum

This power might help expel propellant at 1600 m/s retrograde, which will drop the propellant exhaust plume down to the earth perhaps 11 hours later (and before the loop and its next launches rotate into the tenuous plume). This initially generates 14.4 kN of thrust, reducing the propellant feed as power diminishes, a total impulse of 144 kN-s.

We must generate 856 kN-s more thrust and momentum by other means during vehicle capture, requiring a total energy of perhaps 1.8 GJ. At 100 Wh/kg, that is 5000 kg of fast-discharge lithium-ion battery. Total propellant used is 1000 kN-s / 1600 m/s or 625 kg of inert propellant; perhaps water, 12.5% of incoming vehicle mass. Perhaps 1 in 6 of the incoming vehicles are water tankers.

2000 km/s exhaust molecules would be launched into a retrograde Earth orbit, and plague LEO satellites and subsequent loop launches. A plume launched retrograde with significant additional earthwards velocity will have the same angular momentum and will probably still miss the atmosphere, merely doing so more quickly.

A much faster retrograde exhaust plume velocity, such that the slowest molecules are moving faster than 4.3 km/s relative to the station, will launch the propellant entirely away from the Earth faster than escape velocity. That may require a 5000 m/s or better electric thruster and perhaps 6 GJ of stored battery energy and 17000 kg of battery. It is cheaper to launch more water with the launch loop.

Docking Station to Construction Station

Multiple docking stations may be attached by transfer elevator tethers to the main Construction Station, allowing multiple captures per sidereal day. One way to arrange the tethers is as a rotating "pinwheel" around the construction station, connected by fairly long tethers, helping protect the construction station from errant incoming vehicles. The rotation period may be fairly slow, perhaps a few revolutions per sidereal day, but fast enough to keep them taut as the capture station travels around its highly elliptical orbit. Without rotation, the docking station cables will slacken, making transfer elevator operations more difficult.

The construction station itself may include a one gee centrifugal wheel habitat, encased in a very slowly rotating shielding sheath that attaches to the docking stations; axis oriented north-south. A 50 meter radius, 0.9 gee habitat might turn in 15 seconds; 4 RPM, or 5744 turns per sidereal day. The outer shell might turn every 900 seconds, about 96 times per sidereal day. The centrifugal gravity at the end of 300 meter radial tethers would be 0.015 m/s², or 1.5 milli-gees, and a rotation velocity of 2 meters. This is enough for orientation, but not enough to fling careless workers far from construction station. This rotates the docking stations through a 900 second group of arriving vehicles, discussed in the next section. A 1 m/s² freight elevator can lift captured vehicles to the construction station hub in one minute, including low-jerk starts and stops.

---

Multiple vehicles per day to a one sidereal day construction orbit

Vehicles can be launched from the launch loop into higher apogee orbits over a ±15 minute window around the prime orbit; they will arrive with a bit more tangential velocity, and far more radial velocity. Vehicles launched before the prime orbit time will arrive with downward radial velocity; vehicles launched after the prime orbit time will arrive after.

I presume the vehicles will be as cheap and as close to passive and uncomplicated as possible, and will arrive near the station to be captured by an active maneuvering tether. They will be perturbed somewhat by the turbulent passage out of the thin remaining atmosphere after a high precision launch by the launch loop, and some way of thrusting them into an exactly precise (to millimeters absolute position and micrometers per second relative velocity) is needed.

• My guess is that a reusable "thrust panel" consisting of a "black" laser-absorbent refractory metal sponge, saturated (somehow) with lots of hydrogen, can be designed to eject that hydrogen at very high velocity when it is smacked by a laser pulse from an orbiting station with very big optics. Wild handwaving, but a laser propulsion genius like Leik Myrabo or Jordin Kare might have some good ideas about how to do it (is Jordin's collaborator Tom Nugent still active?). Depleted panels will be returned to Earth for recharge and resuse, or used for bulk shielding.

  An ablative rubber panel might also work, but might scatter too much material into persistent retrograde orbits and pollute low-Earth orbital space with ram-surface-eroding material. A '''No Gram Left Behind''' policy will be necessary for a permanent gigatonne/year spacefaring civilization.

When vehicles arrive, they will be "lassoed" by a velocity and position-matched loop on a deployed cable. They will pull the cable against a drum and a generator, producing electricity to drive some form of propulsion attached to the station itself. We do not need high ISP, but propellant plumes with tightly constrained velocity profiles will be designed to launch all of the propellant into a retrograde orbit with a perigee below the top of the atmosphere. An inert material like argon might be best, so it does not upset upper atmosphere chemistry too much.

Vehicles arriving at ± 900 seconds will have radial velocities around 660 m/s, or excess kinetic energies of 220 kJ/kg; if that was converted 50% efficiently to propellant kinetic energy, a 10% propellant fraction could be launched retrograde at ≈1500 m/s, an impulse of 150 kg-m/s per vehicle kg, more than enough to restore station momentum "lost" to a vehicle capture. A 670 m/s combined radial and tangential velocity capture is frightening - or perhaps "a mere engineering detail", as antimatter propulsion advocate Bob Forward was fond of saying. I don't know how to do it safely and reliably, but someone reading this may be inspired to learn how.

If the expelled propellant fraction is 10%, we can guess that perhaps one in eight of the incoming vehicles are tankers delivering liquid (argon?) propellant.

Early and Late Launch

The prime orbit is easiest to compute, and is coplanar with the construction orbit, but there are other trajectories from the launch loop to the construction station, launching earlier or later from prime launch time. A fully-powered launch loop can launch a 5 tonne vehicle every 45 seconds; over a +/- 900 second window, that is 40 additional vehicles and 200 extra tonnes to the construction station every sidereal day.

A launch loop oriented along the 8 degree south latitude line launches into a plane defined by that velocity vector and the center of the Earth. The launch plane rotates, and orbits launched into one plane will need some north/south delta V to transition to a different plane; for example from an early or late launch into the prime launch plane that also defines the construction orbit.

Over 24 sidereal hours (86164 seconds), the normal vector rotates around the pole with a circle with a radius of sin(8°) on the unit sphere. The angular spacing on that circle from the "prime" launch orbit is the plane change required from a launch at an earlier or later time.

For example, for a launch 900 seconds later, the Earth has turned 360*900/86164 = 3.76°. That is an angle of sin(8°) × sin(3.76°) or 9.13 milliradians around that circle. The plane change velocity near apogee is 2 x sin( 0.5 x 9.13 mrad ) x V_apogee. V_apogee is approximately 900 m/s for a one day construction launch orbit, so the plane change velocity would be approximately 8.2 m/s northward. Similarly, for a launch only 300 seconds after the prime launch orbit, the angle is 3.04 mrad and the plane change velocity is 2.7 m/s northward.

The apogee of an early launch occurs east of the construction orbit perigee, and so does the plane change. The plane change for and apogee of an early launch occurs west of the construction orbit perigee. Assuming a north-south thrust for plane change, and no radial or in-plane thrust, we can remap the problem onto one plane, and compute the intersection of the launch orbit and the construction orbit.

We can change the apogee of the launch orbit by adjusting the loop exit velocity. A slightly higher apogee and velocity requires exiting the loop slightly further east; for now we will ignore this complication and assume all launches occur at the same longitude on the Earth as the prime launch.

---

The Earth rotates 360 degrees in a 86164 second sidereal day, or 3.7603 degrees in 900 seconds. Since C programs and spreadsheets prefer radians, that is 6.5629E-02 radians in 900 seconds, or 7.292116e-5 radians per second. Launching after prime orbit launch results in an apogee to the east of construction and prime orbit apogees (0 degrees or 0 radians); counterclockwise when viewed from the north. Launching before the prime orbit results in an apogee to the west (clockwise when viewed from the north). If the apogee of the candidate orbit is above the radius of the construction orbit at that angle, the two ellipses will intersect at two angles, west and east of that angle.

The candidate launch orbit (hereafter, for this section, launch orbit ) will have less angular momentum than the construction orbit, so at the same radius, the westward orbital velocity will be somewhat less (roughly 10% less, approximately 100 m/s). That means that where the orbits cross, the curvatures differ; the launch orbit is more curved, and the radial accelerations are higher for the launch orbit. Near the west crossing, the vehicle in the launch orbit will be descending (towards the Earth) relative to the construction orbit; near the east crossing, the vehicle ascends.

The construction orbit perigee is (8378-6458) = 1920 km higher than the candidate launch orbit perigee (at launch loop exit), so if the launch orbit is less than 1920 km higher than the construction orbit, 77870 km, it will have a smaller semimajor axis and less than a 86164 second orbital period. By choosing a higher or lower launch apogee, we can choose a longer or shorter delay to apogee. A higher launch velocity results in a higher apogee, and (paradoxically) a longer time delay to apogee.

The western crossing is after launch orbit apogee; given the slower launch orbit velocity, it will cross the construction orbit much later. The eastern crossing is before launch orbit apogee, and will cross the construction orbit sooner.

Our goal is to adjust the launch velocity (and thus the apogee radius) so that the launch vehicle crosses the construction orbit at the same time as the construction station.

• More or less; we will actually aim at a capture device a few kilometers from a docking station attached to the construction station. The actual positions will be tweaked for apsidal precession, lunar and solar and Jupiter tides, and a host of other small perturbations. Those tweaks will be computed and optimized for large ensembles of launched vehicles during launch scheduling; this keeps trajectory design engineers employed, and gives the programmers something to miscalculate . "Orbital accountant" will be a job title, and they will not graduate from orbital accountancy school until they risk their lives travelling an outbound and homewards trajectory they've designed for themselves.

So, given the parameters for a launch orbit:

• perigee time t_{pL} (the launch time, approximately 12 hours before construction orbit apogee time t=0

• apogee angle \theta_L (determined by launch or perigee time)

• apogee radius r_{aL} (determined by launch velocity)

• perigee radius r_{pL} = 6458 km, (launch loop exit radius)

• semimajor axis a_{L} = ( r_{pL} + r_{aL} ) / 2

• eccentricity e_L = ( r_{pL} - r_{aL} ) / ( r_{pL} + r_{aL} ) ~~ negative, relative to apogee

... we have fully specified the launch orbit, and can compute orbit period, apogee time, and the position and velocity vectors as a function of time.

The construction orbit is specified as before; perigee radius r_{pC} = 8378 km, apogee radius r_{ac} = 75950 km, apogee angle \theta_C = 0°, apogee time t_{aC} = 0 seconds. As before, the calculated period is t_C = 86164 seconds (one sidereal day), the semimajor axis is a_C = 42164 km (the same as a circular geostationary orbit), and the eccentricity is e_C = -0.8013 .

Given the orbit apogee angle \theta_C, we can compute the minimum launch apogee radius from the construction orbit radius at that angle:

r_{aL-min} = (1 - {e_C}^2 ) r_{aC} / ( 1 + e_C \cos( \theta_C ) )

The minimum radius is r_{aC} \approx 75950 km for t_{aC} = 0 seconds. For a launch time 900 seconds before prime launch, the launch angle \theta_L is ( 2 \pi 900 / 86164 ) = -0.065629 radians = +3.76° (positive is westward in the eastern Pacific), and for 900 seconds after prime launch, the launch angle \theta_L is -0.065629 radians = -3.76°. In either case, the minimum launch apogee radius must be greater than 75296 km to insure two intersection points.

Given the coplanar launch and construction ellipses, we can:

• 1 compute the two angles at which they intersect
• 2 For each intersection angle, we can compute the arrival time of both the construction station and the launch vehicle
• 3 Then we raise or lower apogee and recompute.

Repeat until one of the time differences is zero; that defines a rendezvous in time and space.

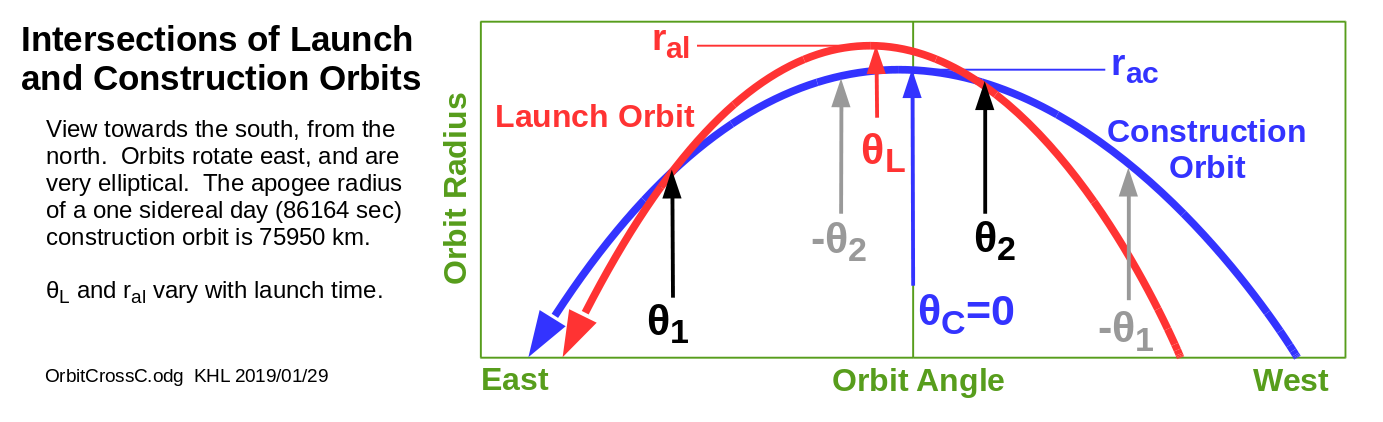
Let's guess a candidate launch orbit apogee r_{aL} . We will find the angles where the radii of launch and construction orbits are the same by equating their radii and computing the angles \theta_1, \theta_2 where this happens.

Starting with r_{pC} = 8378 km, r_{aC}=75950 km, r_{pL} = 6458 km, and r_{aL} TBD, compute the semimajor axes and eccentricities of the two orbits:

For the radius to be the same, the two orbit equations are equal:

~~~ r(\theta) ~=~ { \Large { { ( 1 - {e_L}^2 ) ~ a_L } \over { 1 + e_L \cos( -\theta_L + \theta ) } } } ~=~ { \Large { { ( 1 - {e_C}^2 ) ~ a_C } \over { 1 + e_C \cos( \theta ) } } }

Solving for \theta is easier if we define an intermediate constant: ~~~ K ~=~ { \Large { { ( 1 - {e_L}^2 ) ~ a_L } \over { ( 1 - {e_C}^2 ) ~ a_C } } }

So that: ~~~ K ( 1 + e_C \cos( \theta ) ) ~=~ 1 + e_L \cos( -\theta_L + \theta )

Rearranging: ~~~ \cos( - \theta_L + \theta ) ~=~ ( K - 1 ) /e_L + ( K e_C / e_L ) \cos( \theta )

"Take apart" the first cosine term using the trig identity ~~~ \cos( x + y ) = \cos(x) \cos(y) - \sin(x) \sin(y) :

~~~ \cos( -\theta_L ) \cos( \theta ) - \sin( -\theta_L ) \sin( \theta ) ~=~ \cos( \theta_L ) \cos( \theta ) + \sin( \theta_L ) \sin( \theta ) ~=~ ( K - 1 ) / e_L + ( K e_C / e_L ) \cos( \theta )

We know all the terms except \cos( \theta ) and \sin( \theta ) ; how do we solve for those? Let's solve the equation for \cos( \theta ) in terms of the constants and \sin ( \theta ) :

~~~ \cos( \theta_L ) \cos( \theta ) - ( K e_C / e_L ) \cos( \theta ) ~=~ ( K - 1 ) / e_L - \sin( \theta_L ) \sin( \theta )

~~~ ( \cos( \theta_L ) - ( K e_C / e_L ) ) \cos( \theta ) ~=~ ( K - 1 ) / e_L - \sin( \theta_L ) \sin( \theta )

~~~ \cos( \theta ) ~=~ \Large { { ( K - 1 )/ e_L ~-~ \sin( \theta_L ) \sin( \theta ) } \over { \cos( \theta_L ) - K e_C/e_L } } ~=~ \Large { { ( K - 1 ) ~-~ e_L \sin( \theta_L ) \sin( \theta ) } \over { e_L \cos( \theta_L ) - K e_C } } ~=~ { \Large { { ( K - 1 ) \over { e_L \cos( \theta_L ) - K e_C } } } } ~-~ { \Large { { e_L \sin( \theta_L ) } \over { e_L \cos( \theta_L ) - K e_C } } } \sin( \theta )

Define three more intermediate constants:

~~~~~~ D = e_L \cos( \theta_L ) ~-~ K e_C ~~~~~ and ~~~~~ M = { \Large { { K - 1 } \over D } } ~~~~~ and ~~~~~ N = { \Large { e_L \sin( \theta_L ) \over D } }

So: ~~~~~ \cos( \theta ) = M ~-~ N \sin( \theta ) ~~~~~ Square that: ~~~~~ \cos( \theta )^2 = M^2 ~-~ 2 M N \sin( \theta ) ~-~ N^2 \sin( \theta )^2

Replace: ~~~ 1 - sin^2 = cos^2 ~~~ and get rid of the cos term(!): ~~~ 1 - \sin( \theta )^2 ~=~ M^2 - 2 M N \sin( \theta ) ~+~ N^2 \sin( \theta )^2

Collect terms: ~~~ ( 1 + N^2 ) \sin( \theta )^2 - 2 M N \sin( \theta ) + ( M^2 - 1 ) ~=~ 0

Define even more constants: ~~~ A = 1 + N^2 ~~~~~ B = - 2 M N ~~~~~ C = M^2 - 1

Now we can compute \sin( \theta ) using the binomial formula:

\sin( \theta ) ~=~ { \Large { { -B \pm \sqrt { B^2 - 4 A C } } \over { 2 A } } } ~=~ { \Large { { 2 M N \pm \sqrt { 4 M^2 N^2 - 4 (1 + N^2) ( M^2 - 1 ) } } \over { 2 ( 1 + N^2 ) } } } ~=~ { \Large { { M N \pm \sqrt { M^2 N^2 - M^2N^2 - M^2 + N^2 + 1 } } \over { 1 + N^2 } } }

~~~~~~~~~=~{ \Large { { M N \pm \sqrt { 1 + N^2 - M^2 } } \over { 1 + N^2 } } }

There may be two solutions for \theta , or no solutions if the denominator of either equation is zero, or the second equation is greater than 1.

Starting with a candidate apogee, this produces '''two'' crossing point angles. For each angle, we can compute the time from construction orbit and launch orbit apogees with:

Empirically, for a negative starting time and westward launch angle from the prime orbit, a solution can be found with the smaller of the two positive values of \theta from the sin(\theta) equation above. The launch vehicle arrives at the construction station somewhat slower and from "above". For a one day construction orbit with a 8378 km perigee, the tangential velocity deficit is around 114 m/s and the radial velocity ranges from zero, up to -300 m/s (inwards) for a 900 second early (negative) start time. Because the \theta angle is positive, the vehicle arrives after the launch apogee, "stretching" the time between launch and capture. Since the launch orbit has a shorter period than the construction orbit, this allows for a rendezvous in time and space.

However, for a positive starting time, the crossing point is between the apogees of the launch and construction orbits; \theta is negative, and the launch trajectory time "shortened" between launch and capture. The vehicle arrives too early for a rendezvous for any crossing angle.

Fortunately, a cheap way to stretch the positive-start vehicle arrival time is to increase apogee so that the semimajor axis is larger than the FIXME

---

HERE

Arrival Times for Launch and Construction orbits

POSITIVE TIMES BOGUS, add a small boost and extra orbits, FIXME

Fortunately, cargo vehicles launched over a 30 minute time window arrive over a 49 minute time window, with late and early launches delivering outward and inward radial momentum. With judicious tweaking of launch times and velocities, they can be delivered at regular intervals, with exactly compensating radial momentum. If a "tailhook" cable capture system is practical, this will eliminate the need for high-ISP per-vehicle rockets, making the cargo vehicles more reliable and less expensive. They will require makeup thrust on the construction station itself; with ample solar power and high I_SP electric engines, the station rocket system can be robust, efficient, and multiply redundant.

A relatively small amount of "north-south" thrust will be needed for plane change, less than 10 m/s per vehicle. This thrust is applied hapfway in time between construction station and vehicle apogees, well before capture (CHECK THIS, vehicle apogee time increases with apogee).

---

---

Fix the below

The first table describes a series of increasingly higher altitude construction orbits, with periods that are multiples of sidereal days, synchronizing the orbit with the launch loop as it rotates below.

The first "one sidereal day" orbit will be convenient for the construction of space solar power satellites in synchronous orbits. There may be as many as 96 construction station orbits, spaced around the "sidereal clock", fed by separately synchronous vehicle streams. The quickest return to Earth (say, to return a stabilized accident victim to a hospital on earth) will be from the one day orbit, with a 116 m/s retrograde delta V to drop perigee to 50 km reentry altitude in the atmosphere.

If the launch is not captured by the construction station, the vehicle will be in a shorter period orbit and not synchronize with the station on it's next pass. A 2 m/s retrograde delta V from the launch orbit will also drop perigee to 50 km reentry altitude.

The larger long period orbits will be suitable for the launch of interplanetary missions. They will suffer from larger tidal effects from the moon. Still, if the 5 day orbit at the bottom can be made to work, then the capture delta V will be a mere 40 m/s. After an interplanetary vehicle is assembled in this long period construction orbit and the interplanetary trajectory window opens, the perigee is lowered to perhaps 222 km altitude (6600 km radius) with a 37 m/s thrust at apogee. 2.5 days later at perigee, a 1.1 km/s delta V rocket burn can launch the assembled vehicle with an escape velocity excess vinf = 5.5 km/s for rendezvous with an Aldrin Mars cycler orbit. The referenced paper is for a spartan 75 metric tonne cycler; a vehicle built with 20 4-tonne additions every 5 days over a two year period could mass more than 10,000 tonnes, adding to a vast, shielded wheel suitable for centuries of continuous occupation.

---

Launching from a Construction Orbit to Mars

If an interplanetary vehicle accelerates to a velocity greater than escape velocity at that orbital radius, the excess velocity results in a velocity distant from the Earth of v_{\infty} . ( "Vee infinity" ). For interplanetary launches, higher v_{\infty} reduces travel time, though the arrival velocity can be quite high, which leads to high gee loads entering atmospheres like Mars. The escape velocity at a radius r from the Earth is v^2_{esc} = 2 \mu / r . Given a starting velocity v_r at radius r , v_{\infty}^2 = v_r^2 - 2 \mu / r A small change in v_r can lead to a sizable v_{\infty} . v_{\infty}

Interplanetary launches will begin at the construction orbit apogee, with a small retrograde thrust to drop perigee close to the Earth, maximizing perigee velocity. That maximizes the boost effect of additional delta V at perigee; think of this as adding gravitational energy to the expended propellant, and maximizing the effect of thrust, thus achieving the desired v_{\infty} with a minimum of propellant.

A Hohmann trajectory to Mars results from a v_{\infty} of 2.9 km/s. Consider an "injection orbit" starting at the one day construction orbit apogee radius r_{ca} = r_{ia} = 75950 km. with an injection orbit perigee radius r_{ip} of 6500 km ( 122 km altitude ), for a semimajor axis s_a = 41225 km. The The injection orbit apogee velocity v_{ia} is:

v_{ia} = \sqrt{ ( \mu / s_i ) ( r_{cp} / r_{ca} ) } = \sqrt{ ( 398600.4418 / 41225 ) ( 6500 / 75950 ) } = 0.90966 km/s

The retrograde injection delta V is 1021.18-909.66 m/s = -112 m/s. Hopefully, the propellant plume will have a velocity on the order of -1600 m/s, so that most of the exhaust plume molecules re-enter, that is, have a perigee within the upper atmosphere. 1600 m/s is a low Isp < 180 seconds, so this should use a low energy propellant mixture, perhaps LH/LOX with injected water.

The insertion orbit perigee velocity is:

v_{ip} = \sqrt{ ( \mu / s_c ) ( r_{ca} / r_{cp} ) } = \sqrt{ ( 398600.4418 / 41225 ) ( 75950 / 6500 ) } = 10.629 km/s

for a v_{\infty} = 2.9 km/s, the interplanetary transfer orbit perigee velocity v_{tp} must be:

v_{tp} = \sqrt{ 2.9² + 2 × 398600.4418 / 6500 } = 11.448 km/s

So, the delta V from insertion orbit perigee to an interplanetary Hohmann to Mars is ( 11448 - 10629 ) = 819 m/s, and the total delta V starting at construction orbit perigee is 931 m/s, far less than the ≈11000 m/s direct rocket launch velocity from the Earth's surface.

A more likely mission launched from a construction is a massive 300,000 tonne "Island One" scale permanent habitat, constructed over years in the construction orbit, launched with a crew of thousands into a permanent Aldrin Mars Cycler orbit. This crew will finish the construction and preparation of a Deimos colonization mission, and deploy hundreds of entry vehicles to slow down in the thin Mars atmosphere, and orbit Mars until they are sequentially landed on Deimos to construct a large Deimos scientific colony. A subsequent visit years later by the Mars cycler will deliver the crew for the colony and their supplies.

Mars and Earth have a 782.0 sidereal day (779.9 solar day) synodic period; that enough time to deliver 32,000 vehicles, or 160,000 vehicle-tonnes to more than 40 construction stations from a minimum-sized fully-powered (6GW) launch loop. That is many HUGE missions. A Deimos Synchrotron Light Source ("DSLS") facility for advanced bio-molecule characterization might weigh 30,000 tonnes. A 6 GW space solar power satellite might mass 60,000 tonnes at 10 kg/kW, and require an additional 60,000 tonnes for deployment systems, stationkeeping, and propellant.

---

MoreLater