|
Size: 9252
Comment:
|
Size: 14072
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 5: | Line 5: |
| Superconductors seem like magic to many people. They are perceived as a metal conductor extrapolated zero resistance. Sadly, superconductors are NOT magic, and the realities of their behavior limits their usefulness for the launch loop. | Superconductors seem like magic to many people. They are perceived as a metal conductor extrapolated to zero resistance. In reality, superconductors are NOT magic, and their actual quirky behavior limits their usefulness for new technologies such as the launch loop. |
| Line 7: | Line 7: |
| There are many good books on superconductors, such as "Engineer's Guide to High Temperature Superconductivity" by James Doss, Wiley 1989. I studied superconducting electronics under Ted Van Duzer at UC Berkeley, and my thesis was about superconducting logic. I forgot most of it, but remember a few key points: | There are many good books on superconductors, such as "Engineer's Guide to High Temperature Superconductivity" by James Doss, Wiley 1989. I studied superconducting electronics under Ted Van Duzer at UC Berkeley, and my thesis was about superconducting logic. I now work with billion transistor chip designs. My superconductor memories are out of date and mostly forgotten, but I still remember a few key points, and share them below. ''Note to purists: the following conflates fields (H, measured in amps per meter) and flux (B measured in Tesla or Gauss). So does much of the literature, sigh. I am simplifying greatly, though I fear this essay will still be too complicated for many readers.'' |
| Line 11: | Line 13: |
| Superconductors are macroscopically quantum-ordered collections of free electron and phonons (vibration quanta) in various materials; metals, alloys, and ceramics. They occur at low temperatures, where thermal energy does not disrupt delicate quantum couplings in these collections. All superconductors contain both ordered "superconducting" electrons and normal electrons - both are subject to electrical and magnetic fields, but only the superconducting electrons exhibit zero resistance in limited conditions. Superconductivity can be quenched by a combination of magnetic fields and temperature. The maximum critical field $ H_c $ is a function of temperature; it is maximum at absolute zero temperature, and zero at the critical temperature $ T_c $. | Superconductors are macroscopically quantum-ordered collections of free electron and phonons (vibration quanta) in certain metals, alloys, and ceramics. Superconductivity appears at low temperatures, where thermal energy does not disrupt delicate quantum couplings. Superconductors exhibit zero (or very low resistance), flux exclusion at low fields, and macroscopic scale quantum effects such as flux quantization. All superconductors contain both ordered "superconducting" electrons and normal electrons - both are subject to electrical and magnetic fields, but only the superconducting electrons exhibit zero resistance. Superconductivity is disrupted excessive currents, magnetic fields and temperature. The maximum critical field $ H_c $ is a function of temperature; it is maximum at absolute zero temperature, and zero at the critical temperature $ T_c $. |
| Line 15: | Line 17: |
| Jumps in resistance in a bulk sample are not a reliable indication of superconductivity - resistance drops with temperature in most conductors, and resistance measurements can be upset by mechanical fixturing and material phase changes as materials cool and contract. For thin films of candidate materials, the best resistance measurement is a "four point" Kelvin measurement, where a thin strip of material is deposited on insulating ceramic or glass, and contacted at the ends to supply a current, and tapped at two points in the middle to measure the voltage drop caused by the current. Even this is not foolproof; this is also the setup for a resistive strain gauge, and differences in thermal expansion can add resistance to the setup, as can microfractures and grain boundary slips in the sample. At best, competent resistive measurements are a cheap way to screen candidate materials for further testing. | Jumps in resistance measurements in a bulk sample are not a reliable indication of superconductivity. Resistance drops with temperature in most conductors, and resistance measurements can be upset by mechanical fixturing and material phase changes as samples and connections cool and contract. For thin films of candidate materials, the best resistance measurement is a "four point" Kelvin measurement, where a thin strip of material is deposited on insulating ceramic or glass, and contacted at the ends to supply a current, and tapped at two points in the middle to measure the voltage drop caused by the current. Even this is not foolproof; this is also the setup for a resistive strain gauge, and indirectly a thermocouple, and differences in thermal expansion or end to end temperature can add voltage drops to the setup, as can microfractures and grain boundary slips in the sample. At best, competent resistive measurements are a cheap way to screen candidate materials for further testing. |
| Line 17: | Line 19: |
| The '''gold standard''' for testing superconductivity is the Meissner effect. Superconductors behave like "diamagnetic" materials at modest magnetic fields; they exclude magnetic flux, making it go around the sample. This can be detected with the right instruments and experimental setups, even if we are measuring little embedded bits of superconductor in a jumble of materials. Meissner effect can be dramatic; it is why a chunk of superconductor will hover above a strong magnet, or vice versa. | The '''gold standard''' for testing superconductivity is the '''Meissner effect'''. Superconductors behave like "diamagnetic" materials at modest magnetic fields; they exclude magnetic flux, making it go around the sample. This can be detected with the right instruments and experimental setups, even if we are measuring little embedded bits of superconductor in a jumble of materials. Meissner effect can be dramatic; that effect is why a chunk of superconductor will hover above a strong magnet, or vice versa. |
| Line 19: | Line 21: |
| If someone claims to have discovered a superconductor based on a fractional percentage resistance change as they cool some aggregate material, they have not completed the task. If they are doing a two-point resistance measurement, especially with cheap ohmmeters, they are almost certainly fooling themselves. Real superconductivity is hard to achieve, but dramatic when it occurs. | If someone claims to have discovered a superconductor based on a fractional percentage resistance change as they cool some aggregate material, they have not completed the task. If they are doing a two-point resistance measurement, especially with cheap ohmmeters, they are almost certainly fooling themselves. Real superconductivity is hard to achieve, and difficult to show with resistance measurements, but the magnetic effects are dramatic when it occurs. |
| Line 23: | Line 25: |
| Pure metals tend to be type 1 superconductors, and have low $ T_C $ and $ H_C $. They are good for superconducting circuitry and sensors, though, where power levels are low and repeatability is important. | Pure metals tend to be type 1 superconductors, and have low $ T_c $ and $ H_c $. They are good for superconducting circuitry and sensors, though, where power levels are low and repeatability is important. |
| Line 29: | Line 31: |
| Again, $ H_c $ decreases with temperature. If the material temperature is half of $ T_c $, $ H_c $ might be 75% of the zero temperature value above. At 80% of $ T_c $, $ H_c $ might be 45% of the zero temperature value above. You can't get both maximum temperature and field at the same time. |
Again, $ H_c $ decreases with temperature. If the material temperature is half of $ T_c $, $ H_c $ might be 75% of the zero temperature value above. At 80% of $ T_c $, $ H_c $ might be 45% of the zero temperature value above. You can't get both maximum temperature and field at the same time. |
| Line 32: | Line 34: |
| These are DC steady-state measurements. Remember that superconductors are a mix of superconducting electrons and normal "resistive" electrons. When you change currents, you produce a voltage field in a conductor due to its inductance. This voltage field moves both kinds of electrons, and while the superconducting electrons conduct most of the current, the resistive electrons produce a current that encounters resistance and dissipates heat. Because the heat capacity and thermal conduction of materials at low temperatures are small, even a small amount of heat can raise the temperature significantly. This increases the fraction of resistive electrons, which increases the heating. | These are DC steady-state measurements. Remember that superconductors are a mix of superconducting electrons and normal "resistive" electrons. When you change currents, you produce a voltage field in a conductor due to its inductance. This voltage field moves both kinds of electrons, and while the superconducting electrons conduct most of the current, the resistive electrons produce a current that encounters resistance and dissipates heat. Because the heat capacity and thermal conduction of materials at low temperatures are small, even a small amount of heat can raise the temperature significantly. This increases the fraction of resistive electrons, which increases the heating. |
| Line 34: | Line 36: |
| This can lead to '''quenching''', where the material heats above $ T sub C $ and heats faster as the resistance climbs with temperature. If the current is constant (typical in large magnets that store a lot of energy) the heat rapidly boils the coolant, creating high pressure gas and eventually an explosion. | This can lead to '''quenching''', where the material heats above $ T_c $ and heats faster as the resistance climbs with temperature. If the current is constant (typical in large magnets that store a lot of energy) the heat rapidly boils the coolant, creating high pressure gas and eventually an explosion. |
| Line 38: | Line 40: |
| === Current depth === | === Current === |
| Line 40: | Line 42: |
| The field and temperature do not tell the whole story. The current in a superconducting wire mostly runs near the surface, within a distance called the London length. This current cannot exceed a critical current $ J_c $, which is a function of magnetic field and temperature. The London length is typically less than a micron. The current capacity of a centimeter diameter solid cylinder of superconductor is not significantly higher than that of a centimeter diameter hollow tube. A bundle of thin wires can carry more current, and are often embedded in a copper or silver matrix. The thermal expansion of copper and superconductor may be significantly different, however, leading to strain and cracking; this is a big problem for the ceramic high temperature superconductors. || {{attachment:CRITSURF.GIF}} || Here is a phase diagram, showing the interdependence of maximum temperature, magnetic field, and current for a type I superconductor || |
|| {{attachment:CRITSURF.GIF}} || The field and temperature do not tell the whole story. The current in a superconducting wire mostly runs near the surface, within a distance called the London length. This current cannot exceed a critical current $ J_c $, which is a function of magnetic field and temperature. The London length is typically less than a micron. The current capacity of a centimeter diameter solid cylinder of superconductor is not significantly higher than that of a centimeter diameter hollow tube. A bundle of thin wires can carry more current, and are often embedded in a copper or silver matrix. The thermal expansion of copper and superconductor may be significantly different, however, leading to strain and cracking; this is a big problem for the ceramic high temperature superconductors.<<BR>><<BR>>The drawing is a phase diagram, showing the interdependence of maximum temperature, magnetic field, and current for a type I superconductor.<<BR>>cite: http://chabanoiscedric.tripod.com/supra.html || |
| Line 46: | Line 46: |
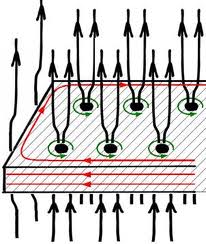
| Alloyed metals and the newer ceramic superconductors are Type II superconductors, with much higher $ T_c $ and $ H_c $. They actually have two critical fields, $ H_c1 $ and $ H_c2 $. Below $ H_c1 $, the material is a Meissner superconductor and fields are excluded, like Type I materials. Above H_c1 and below H_c2, some of the magnetic field penetrates the superconductor through tiny non-superconducting threads or '''vortices'''. These vortexes tend to form a hexagonal lattice, with superconducting material in between. As the magnetic field is increased or decreased, the vortices move in and out of the material, and create significant resistance and heating. | || {{attachment:vortex.jpg}} || Alloyed metals and the newer ceramic superconductors are Type II superconductors, with much higher $ T_c $ and $ H_c $. They actually have two critical fields, $ H_{c1} $ and $ H_{c2} $. Below $ H_{c1} $, the material is a Meissner superconductor and fields are excluded, like Type I materials. Above $ H_{c1} $ and below $ H_{c2} $, some of the magnetic field penetrates the superconductor through tiny non-superconducting threads or '''vortices'''. These vortices tend to form a hexagonal lattice, with superconducting material in between. As the magnetic field is increased or decreased, the vortices move in and out of the material, and create significant resistance and heating. <<BR>><<BR>> As the field approaches $ H_{c2} $, the lattice changes from "glass" to "liquid", and the vortices start randomly jumping around. This also causes resistance, even to DC currents.<<BR>><<BR>>'''The drawing''' shows vortices surrounding field lines in a type II superconductor<<BR>>cite:http://www.supraconductivite.fr/en/index.php?p=supra-levitation-vortex-more <<BR>><<BR>>'''The graph''' shows Field/Temperature phase diagram for superconductors<<BR>>cite:http://jick.net/theses/Price/node6.html || {{attachment:phase.png}}|| |
| Line 48: | Line 48: |
| As the field approaches $ H_c2 $, the lattice changes from "glass" to "liquid", and the vortices start shifting around. This also causes resistance, even to DC fields. | The newer ceramic High Temperature Superconductors are still poorly understood theoretically. They can have critical fields above 100 Tesla, and critical temperatures above 100 Kelvins. Their behavior is more complex, with with '''anisotropic''' (direction dependent) critical currents and fields. They are also quite brittle, not ductile like metals and alloys. HTC superconductors are still mostly experimental, though some companies are selling wire tapes with HTC bonded to copper, brass, or silver in kilogram quantities (not tons) for prototype development. These very high $ T_c $ materials can be used with liquid nitrogen as a coolant at 77K ( -196C or -320F ), but the $ H_c $ and $ J_c $ are lower than they would be at colder temperatures. |
| Line 50: | Line 50: |
| {{attachment:phase.jpg}} | Because HTC materials are complex, difficult to make, and poorly understood, the field is rife with false discoveries, mistakes and retractions. Some poorly equipped foreign labs are especially prone to claim new records for high temperatures, and a few lone individuals in the US are making unlikely claims as well. While we would love for these underdogs to succeed, they are unlikely to do so without proper training, tools, and meticulous lab procedure. Nature rarely reveals its secrets to the careless. |
| Line 52: | Line 52: |
| Even if some of these claims pan out, and even if someone produces the "holy grail" of a room temperature superconductor with a $ T_c $ greater than 300 Kelvin, such speculative materials will still need a high $ H_c $ and $ J_c $ to be useful, will need to be reliably manufacturable, and will '''still require refrigeration''' so they are far enough down the phase diagram to support significant fields and current. A practical room temperature superconductor would need a $ T_c $ greater than 400 Kelvin to use water cooling and exhaust heat to ambient air. That is almost three times higher than repeatable and verified HTC lab results, and almost four times the temperatures of deployed materials. Don't hold your breath ... | |
| Line 57: | Line 56: |
| Magnetic fields are complicated. The $ H $ field near a round wire is proportional to the current, and inversely proportional to the distance. The fields from multiple wires add together, and influence each other. Because of Meissner effect, the fields are pushed out to the edges of a wire and concentrated there - this effect is pronounced in wire tapes and other non-circular wires. | Magnetic fields are complicated. The $ H $ field near a round wire is proportional to the current, and inversely proportional to the distance. The fields from multiple wires add together, and influence each other. Because of Meissner effect, the fields are pushed out to the edges of a wire and concentrated there - this effect is pronounced in wire tapes and other non-circular wires. |
| Line 61: | Line 60: |
| Magnetic fields store energy, proportional to the square of the field times the volume. A cubic meter of volume with a 10 Tesla field in it stores 10 million joules, almost 3 kilowatt hours. | Magnetic fields store energy, proportional to the square of the field times the volume. A cubic meter of volume containing a 5 Tesla field stores 10 million joules, almost 3 kilowatt hours. That is the energy and pressure equivalent of 100 atmosphere compressed air, and the structural demands are similar. |
| Line 63: | Line 62: |
| Magnetic fields also produce tremendous forces on current carrying wires. Two wires with current in the same direction attract each other. Two wires with opposite currents repel. So the fields in a coil want to "explode" the space and dissipate the field, pushing the circumferential wires outwards and away from each other. They also push neighboring wires with currents in the same direction together. The latter increases the field in the wires themselves, and causes resistive heating. Unless superconducting wires are anchored very firmly, they are likely to heat and quench and explode. | Magnetic fields also produce tremendous forces on current carrying wires. Two wires with current in the same direction attract each other. Two wires with opposite currents repel. So the fields in a coil want to "explode" the space and dissipate the field, pushing the circumferential wires outwards and away from each other. They also push neighboring wires with currents in the same direction together. The latter increases the field in the wires themselves, and causes resistive heating. Unless superconducting wires are anchored very firmly, they are likely to move, then heat and quench and explode. === Conclusion === Superconductors are difficult to work with. They have many practical applications, such as sensors, DC magnets, and as part of laboratory and space probe experiments. HTC superconductors appear in prototype motors, generators, maglev trains, and energy storage coils, but they are not widely deployed. It is good to experiment with these materials, but we should not depend on them to make difficult ideas easier; if anything, they add complications and barriers to deployment. As launch volumes approach kilotons per second, waste heat will begin to have noticeable environmental effects, and we may need to reduce heat using reliable technologies. A decade or two after first deployment, launch loops and power storage loops may begin to use DC superconducting deflection magnets, though superconductors will never appear in the high frequency motors, which do not need DC fields or light weight. However, in the short term, robust operation and cheap startup costs are more important, so we can replace rockets as soon as possible. Copper, iron, and cooling water are well understood. We should focus our attention on problems such as stability and hyper-velocity spalling, and developing initial markets for loop technology. We must find solutions for widespread human and environmental problems, not makework for narrowly specialized materials scientists. Launch loop and server sky will create plenty of other material science opportunities. Seek customer dollars, not research grants. |
Superconductors
Superconductors seem like magic to many people. They are perceived as a metal conductor extrapolated to zero resistance. In reality, superconductors are NOT magic, and their actual quirky behavior limits their usefulness for new technologies such as the launch loop.
There are many good books on superconductors, such as "Engineer's Guide to High Temperature Superconductivity" by James Doss, Wiley 1989. I studied superconducting electronics under Ted Van Duzer at UC Berkeley, and my thesis was about superconducting logic. I now work with billion transistor chip designs. My superconductor memories are out of date and mostly forgotten, but I still remember a few key points, and share them below.
Note to purists: the following conflates fields (H, measured in amps per meter) and flux (B measured in Tesla or Gauss). So does much of the literature, sigh. I am simplifying greatly, though I fear this essay will still be too complicated for many readers.
What is a superconductor ?
Superconductors are macroscopically quantum-ordered collections of free electron and phonons (vibration quanta) in certain metals, alloys, and ceramics. Superconductivity appears at low temperatures, where thermal energy does not disrupt delicate quantum couplings. Superconductors exhibit zero (or very low resistance), flux exclusion at low fields, and macroscopic scale quantum effects such as flux quantization. All superconductors contain both ordered "superconducting" electrons and normal electrons - both are subject to electrical and magnetic fields, but only the superconducting electrons exhibit zero resistance. Superconductivity is disrupted excessive currents, magnetic fields and temperature. The maximum critical field H_c is a function of temperature; it is maximum at absolute zero temperature, and zero at the critical temperature T_c .
Detecting superconductivity in experimental materials
Jumps in resistance measurements in a bulk sample are not a reliable indication of superconductivity. Resistance drops with temperature in most conductors, and resistance measurements can be upset by mechanical fixturing and material phase changes as samples and connections cool and contract. For thin films of candidate materials, the best resistance measurement is a "four point" Kelvin measurement, where a thin strip of material is deposited on insulating ceramic or glass, and contacted at the ends to supply a current, and tapped at two points in the middle to measure the voltage drop caused by the current. Even this is not foolproof; this is also the setup for a resistive strain gauge, and indirectly a thermocouple, and differences in thermal expansion or end to end temperature can add voltage drops to the setup, as can microfractures and grain boundary slips in the sample. At best, competent resistive measurements are a cheap way to screen candidate materials for further testing.
The gold standard for testing superconductivity is the Meissner effect. Superconductors behave like "diamagnetic" materials at modest magnetic fields; they exclude magnetic flux, making it go around the sample. This can be detected with the right instruments and experimental setups, even if we are measuring little embedded bits of superconductor in a jumble of materials. Meissner effect can be dramatic; that effect is why a chunk of superconductor will hover above a strong magnet, or vice versa.
If someone claims to have discovered a superconductor based on a fractional percentage resistance change as they cool some aggregate material, they have not completed the task. If they are doing a two-point resistance measurement, especially with cheap ohmmeters, they are almost certainly fooling themselves. Real superconductivity is hard to achieve, and difficult to show with resistance measurements, but the magnetic effects are dramatic when it occurs.
Type I superconductors
Pure metals tend to be type 1 superconductors, and have low T_c and H_c . They are good for superconducting circuitry and sensors, though, where power levels are low and repeatability is important.
material |
Mercury |
Lead |
Niobium |
|
T_c , Kelvin |
4.2 |
7.2 |
9.3 |
at zero magnetic field |
H_c , Tesla |
|
0.08 |
0.18 |
at zero absolute temperature |
Again, H_c decreases with temperature. If the material temperature is half of T_c , H_c might be 75% of the zero temperature value above. At 80% of T_c , H_c might be 45% of the zero temperature value above. You can't get both maximum temperature and field at the same time.
These are DC steady-state measurements. Remember that superconductors are a mix of superconducting electrons and normal "resistive" electrons. When you change currents, you produce a voltage field in a conductor due to its inductance. This voltage field moves both kinds of electrons, and while the superconducting electrons conduct most of the current, the resistive electrons produce a current that encounters resistance and dissipates heat. Because the heat capacity and thermal conduction of materials at low temperatures are small, even a small amount of heat can raise the temperature significantly. This increases the fraction of resistive electrons, which increases the heating.
This can lead to quenching, where the material heats above T_c and heats faster as the resistance climbs with temperature. If the current is constant (typical in large magnets that store a lot of energy) the heat rapidly boils the coolant, creating high pressure gas and eventually an explosion.
To prevent this, superconductors for power lines and magnets are embedded in a much heavier matrix of copper or silver. That adds heat capacity and extra normal conduction path, reducing the sudden transition and giving circuit breakers and arc dissipation systems time to work. That can keep the system from exploding, but not from ceasing to function.
Current
|
The field and temperature do not tell the whole story. The current in a superconducting wire mostly runs near the surface, within a distance called the London length. This current cannot exceed a critical current J_c , which is a function of magnetic field and temperature. The London length is typically less than a micron. The current capacity of a centimeter diameter solid cylinder of superconductor is not significantly higher than that of a centimeter diameter hollow tube. A bundle of thin wires can carry more current, and are often embedded in a copper or silver matrix. The thermal expansion of copper and superconductor may be significantly different, however, leading to strain and cracking; this is a big problem for the ceramic high temperature superconductors. |
Type II and High Temperature Superconductors
|
Alloyed metals and the newer ceramic superconductors are Type II superconductors, with much higher T_c and H_c . They actually have two critical fields, H_{c1} and H_{c2} . Below H_{c1} , the material is a Meissner superconductor and fields are excluded, like Type I materials. Above H_{c1} and below H_{c2} , some of the magnetic field penetrates the superconductor through tiny non-superconducting threads or vortices. These vortices tend to form a hexagonal lattice, with superconducting material in between. As the magnetic field is increased or decreased, the vortices move in and out of the material, and create significant resistance and heating. |
|
The newer ceramic High Temperature Superconductors are still poorly understood theoretically. They can have critical fields above 100 Tesla, and critical temperatures above 100 Kelvins. Their behavior is more complex, with with anisotropic (direction dependent) critical currents and fields. They are also quite brittle, not ductile like metals and alloys. HTC superconductors are still mostly experimental, though some companies are selling wire tapes with HTC bonded to copper, brass, or silver in kilogram quantities (not tons) for prototype development. These very high T_c materials can be used with liquid nitrogen as a coolant at 77K ( -196C or -320F ), but the H_c and J_c are lower than they would be at colder temperatures.
Because HTC materials are complex, difficult to make, and poorly understood, the field is rife with false discoveries, mistakes and retractions. Some poorly equipped foreign labs are especially prone to claim new records for high temperatures, and a few lone individuals in the US are making unlikely claims as well. While we would love for these underdogs to succeed, they are unlikely to do so without proper training, tools, and meticulous lab procedure. Nature rarely reveals its secrets to the careless.
Even if some of these claims pan out, and even if someone produces the "holy grail" of a room temperature superconductor with a T_c greater than 300 Kelvin, such speculative materials will still need a high H_c and J_c to be useful, will need to be reliably manufacturable, and will still require refrigeration so they are far enough down the phase diagram to support significant fields and current. A practical room temperature superconductor would need a T_c greater than 400 Kelvin to use water cooling and exhaust heat to ambient air. That is almost three times higher than repeatable and verified HTC lab results, and almost four times the temperatures of deployed materials. Don't hold your breath ...
Magnetic fields in conductors and magnets
Magnetic fields are complicated. The H field near a round wire is proportional to the current, and inversely proportional to the distance. The fields from multiple wires add together, and influence each other. Because of Meissner effect, the fields are pushed out to the edges of a wire and concentrated there - this effect is pronounced in wire tapes and other non-circular wires.
So if you make a coil of superconducting wire, intending to create a high magnetic field strength in the center, the field near the superconductors themselves may be a large multiple of the field in the center. So, an HTC material with a critical field of 100 Tesla may only be capable of producing a field of 10 Tesla in the middle of a cylindrical coil. This effect is most pronounced when a small bundle of superconducting wire is expected to produce a high field many radiuses away. If you want 1 Tesla 10 meters away, then a bundle of wire 10 centimeters across will have 100 Tesla fields near it, and more at the surface of the wires themselves.
Magnetic fields store energy, proportional to the square of the field times the volume. A cubic meter of volume containing a 5 Tesla field stores 10 million joules, almost 3 kilowatt hours. That is the energy and pressure equivalent of 100 atmosphere compressed air, and the structural demands are similar.
Magnetic fields also produce tremendous forces on current carrying wires. Two wires with current in the same direction attract each other. Two wires with opposite currents repel. So the fields in a coil want to "explode" the space and dissipate the field, pushing the circumferential wires outwards and away from each other. They also push neighboring wires with currents in the same direction together. The latter increases the field in the wires themselves, and causes resistive heating. Unless superconducting wires are anchored very firmly, they are likely to move, then heat and quench and explode.
Conclusion
Superconductors are difficult to work with. They have many practical applications, such as sensors, DC magnets, and as part of laboratory and space probe experiments. HTC superconductors appear in prototype motors, generators, maglev trains, and energy storage coils, but they are not widely deployed. It is good to experiment with these materials, but we should not depend on them to make difficult ideas easier; if anything, they add complications and barriers to deployment.
As launch volumes approach kilotons per second, waste heat will begin to have noticeable environmental effects, and we may need to reduce heat using reliable technologies. A decade or two after first deployment, launch loops and power storage loops may begin to use DC superconducting deflection magnets, though superconductors will never appear in the high frequency motors, which do not need DC fields or light weight. However, in the short term, robust operation and cheap startup costs are more important, so we can replace rockets as soon as possible. Copper, iron, and cooling water are well understood. We should focus our attention on problems such as stability and hyper-velocity spalling, and developing initial markets for loop technology. We must find solutions for widespread human and environmental problems, not makework for narrowly specialized materials scientists. Launch loop and server sky will create plenty of other material science opportunities.
Seek customer dollars, not research grants.