|
Size: 7362
Comment:
|
Size: 14920
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 7: | Line 7: |
| Modern comsats use noble-gas electric thrusters to climb to GEO. This is propellant-thrifty; however, this has driven up the price of Xenon, so usage is shifting to Krypton. There is not enough available high-Z noble gas (xenon, krypton) to raise the orbits of 120 million of tonnes of power satellite. There is plenty of argon, but that must be chilled below 27 Kelvin to store densely for the long spiral orbit to GEO. | Modern comsats use noble-gas electric thrusters to climb to GEO. This is propellant-thrifty; however, this has driven up the price of xenon, so usage is shifting to krypton. There is not enough available high-Z noble gas (xenon, krypton) to raise the orbits of 120 million of tonnes of power satellite. There is plenty of argon, but that must be chilled below 87 Kelvin to store densely for the long spiral orbit to GEO. |
| Line 11: | Line 11: |
| So, consider liquid hydrogen + liquid oxygen ( LH/LOX) chemical rockets, with typical 1:6 mass ratio (slightly fuel rich), producing a propellant plume of and H₂ and H. The mass ratio of water to total hydrogen ( H₂ plus H ), assuming complete combustion and no hydroxyl ( OH or HO ) or hydronium ( H₃O ), is 27:1 . | {{ attachment:AccelerateEllipse.png }} |
| Line 13: | Line 13: |
| Assuming a high expansion vacuum nozzle, the exhaust velocity of a liquid hydrogen engine might be as high as 4460 m/s. | So, consider liquid hydrogen + liquid oxygen (LH/LOX) chemical rockets, with typical 1:6 mass ratio (slightly fuel rich), producing a propellant plume of and H₂ and H. The mass ratio of water to total hydrogen ( H₂ plus H ), assuming complete combustion and no hydroxyl ( OH or HO ) or hydronium ( H₃O ), is 27:1. Ignore the hydrogen and presume the entire plume is H₂O. |
| Line 15: | Line 15: |
| Spacecraft typically launch to GEO from low earth orbit (LEO) via a geostationary transfer orbit (GTO). Presume that the GTO perigee starts from a 122 km equatorial altitude so that the GTO is an ellipse with perigee = 6500 km, apogee = 42164 km, semi-major axis 24332 km. The apogee velocity of the GTO ellipse is 1589 m/s. The GEO circularization delta V is (3075-1589) = 1486 m/s . | Assuming a high expansion vacuum nozzle, the exhaust velocity of a LH/LOX engine might be as high as 4460 m/s. Spacecraft typically launch to GEO from low earth orbit (LEO) via a geostationary transfer orbit (GTO). Presume that the GTO perigee starts from a 122 km equatorial altitude so that the GTO is an ellipse with perigee radius = 6500 km, apogee radius = 42164 km, semi-major axis 24332 km. The apogee velocity of the GTO ellipse is 1589 m/s. The GEO circularization delta V is (3075-1589) = 1486 m/s . |
| Line 27: | Line 29: |
| Well, to start with, we know a retrograde orbit with a velocity of 1589 m/s has a perigee of 122 km; slower species will descend to a lower altitude and fall into the atmosphere. Species with a retrograde velocity of 2871 m/s will have an perigee of 32600 km, and will remain above the atmosphere for a very long time. Species with a retrograde velocity of 1640 m/s will have a perigee above 600 km, and will remain in orbit for decades. | Well, to start with, we know a retrograde orbit with a velocity of -1589 m/s has a perigee of 122 km; slower species will descend to a lower altitude and fall into the atmosphere. Species with a retrograde velocity of -2871 m/s will have an perigee of 32600 km, and will remain above the atmosphere for a very long time. Species with a retrograde velocity of -1640 m/s will have a perigee above 600 km, and will remain in orbit for decades. |
| Line 29: | Line 31: |
| Lets consider the portion of the plume emitted between 1640 m/s and 2871 m/s to be in semi-permanent orbits, and the portion of the plume emitted between 1589 m/s and 1640 m/s to re-enter and stop being a problem. If the plume is 1640 m/s retrograde, the vehicle is travelling 4460-1640 = 2820 m/s prograde. So, the re-entering portion of the plume is the fraction emitted while the vehicle accelerates from 2820 to 3075 m/s, a delta V of 255 m/s. Let's use the Tsiolkovsky equation for that: | Lets consider the portion of the plume emitted between -1640 m/s and -2871 m/s to be in semi-permanent orbits, and the portion of the plume emitted between 1589 m/s and 1640 m/s to re-enter and stop being a problem. If the plume is -1640 m/s retrograde, the vehicle is travelling 4460-1640 = 2820 m/s prograde. So, the re-entering portion of the plume is the fraction emitted while the vehicle accelerates from 2820 to 3075 m/s, a delta V of 255 m/s. Let's use the Tsiolkovsky equation for that: |
| Line 33: | Line 35: |
| So, the plume emitted into semipermanent orbits is (47-7)e9 = 40e9 kg. | So, the plume emitted into semi-permanent orbits is (47-7)e9 = 40e9 kg = 4e10 kg. Mostly water molecules, atomic weight 18, 3.35e25 molecules per kilogram, for a total of 1.3e36 molecules. Their orbital periods will range from 9 to 20 hours, so the average particle will return to orbit apogee every 50,000 seconds. '''Orbits with an apogee at ~+__GEO!__+~''' |
| Line 35: | Line 37: |
| '''Orbits with an apogee at ~+__GEO!__+~''' Over those years, many ''(most?)'' of those species will collide with the ram (forward orbit facing) surfaces of the SSPS, at velocities up to 5946 m/s (3075 + (4460-1589)) slowing them and sputtering the ram surface. An H₂O molecule with a mass of 18 AMU (3e-26 kg) and a relative velocity of 5946 m/s has a kinetic energy of 5.3e-19 J or 3.3 electron volts. For comparison, monatomic oxygen in 500 km LEO ( orbit speed has a kinetic energy of 7.7-19 J or 4.8 eV, is vastly less dense, and is a known long term hazard to much denser objects than an SSPS. | The flux rate through the entire GEO region is 2.6e31 molecules per second. If the molecules are in an average 50,000 second orbit (29334 km semimajor axis, ), their "dwell time" at a radius 10 km from apogee is 140 seconds, hence 0.28% of the molecules, or 3.6e33 molecules, are in a narrow "GEO torus" at any given time moving retrograde relative to the SSPS constellation at a (3075+2306) = 5381 m/s. The volume of that torus is . . . MoreLater (a better analysis involving dwell time) |
| Line 37: | Line 39: |
| This is an "N squared" problem. Delivering 1500 tonnes of GEO comsat with a 500 tonnes of propellant plume is a 6400 times smaller problem. The comsats are much denser than an SSPS, reducing the collision cross section. We have not encountered any '''major''' problems yet - unless plume collision erosion is responsible for a few unexplained losses ... :-( | Over those years, many ''(most?)'' of those species will collide with the ram (forward orbit facing) surfaces of thousands of kilo-hectare power satellites, at velocities up to 5946 m/s (3075 + (4460-1589)) slowing them and sputtering the ram surface. An H₂O molecule with a mass of 18 AMU (3e-26 kg) and a relative velocity of 7344 m/s has a kinetic energy of 5.3e-19 J or 3.3 electron volts. This can damage the power satellites. For comparison, mono-atomic fringe-atmosphere oxygen at 500 km altitude above the 6371 km radius earth (6871 km) rotates with the earth at a velocity of 500 m/s. ISS (in a 54 degree inclined orbit) orbits at 7617 m/s. It encounters oxygen atoms while it crosses the equator at a relative velocity of (coincidentally!) 7344 m/s, with an impact energy of 3.1 eV. This slows ISS, requiring periodic thrust for reboost, and also sputters material off the ram surface of ISS, a known long term hazard. Worse yet, a significant fraction of the plume atoms will have retrograde perigees at LEO, where there will be assets orbiting prograde. While a relatively small fraction of the plume emitted at GEO (with apogee at GEO) will (coincidentally) have perigees near important LEO assets, where they do, the velocity differences will be huge. Consider the International Space Station, ISS, in a circular LEO orbit with an "altitude" of 500 km, presumably a 6870 km radius orbit, inclined 54 degrees. Consider an H2O plume molecule in a 42164 by 6871 km orbit; it will have a perigee velocity close to 10 km/s. The closing velocity with ISS as it crosses the equator is 14.8 km/s, and the collision energy for an H2O molecule will be 20 eV, '''six times higher''' than the collision velocity for atomic oxygen. If the plume is dense, it could be catastrophic to LEO objects. For objects in a prograde transfer orbit to GEO, the closing velocity will be 20 km/s, the collision energy will be 36 eV, huge, though hopefully objects in transfer orbits will only encounter this onslaught one time. This is an "N squared" problem. Delivering 1500 tonnes of GEO comsat with a 500 tonnes of propellant plume is a '''6 billion times smaller''' problem. The comsats are much denser than an SSPS, reducing the collision cross section even further. We have not encountered any '''major''' problems with our comsat fleet yet - unless plume collision erosion is responsible for a few unexplained losses ... :-( === Ionization, Charged Particle Trapping on Field Lines === Accroding to [[ https://spacemath.gsfc.nasa.gov/earth/RBSP7.pdf | this NASA "space math" exercise ]], the van Allen belts contain only '''two grams''' of protons (ionized hydrogen) at very high energy, a density averaging 1e-5/cm³ = 10/m³ in a 1e23 m³ volume out to 6 Re (I'm skeptical, but don't have a better source). GEO is 6.6 Re; lets assume the GEO insertion plume region is a spherical shell 200 km thick, a volume of 4.5e21 cubic meters. Electric engines produce ions (like the Van Allen belts) so those can be trapped by field lines as well. The Earth dipole produces a field in the equatorial plane of $ B = B_0 ( Re / R )^3 $ where $ R $ is the radius, $ B_0 $ = 3.12e-5 Tesla and $ Re $ = 6.371e6 meters. At 6.6 Re, the field is 1.1e-7 Tesla. The cyclotron radius for a charged particle is $ r = m v / q B $; for an N amu (amu = 1.6e-27 kg, q = 1.6e-19 colombs ) particle at GEO the cyclotron radius $ r $ is ( 0.085 sec * N * v meters ), where v is "the" exhaust molecule velocity. Here's a table of retrograde velocity and N for plausible exhaust species (minus the estimated "average" 2300 m/s prograde velocity of the GEO-orbit insertion rocket emitting them): ||<-10> Cyclotron radius at 6.2 Re GEO "average" velocity || Number || || '''Scenario''' || species || N || size || v || Radius || Mass ||<-2> Molecules || Mean free || Density || || || || || pm || km/s || km || kg || total || per m3 || path μm || Altitude || || LOX/LH2 || H₂O || 18 || 270 || 2.2 || 3.4 || 4e10 || 1.4e36 || 3.1e14 || 12 || 338 km || || Hydrogen Arcjet || H₂ || 2 || 290 || 8 || 1.4 || 1e10 || 3.1e36 || 6.9e14 || 5 || 297 km || || Teflon ablator || CF || 31 || xxx || 10 || 26 || 8e9 || 1.6e35 || 3.6e13 || || 466 km || || Argon Helicon || Ar || 40 || 340 || 20 || 68 || 4e9 || 6.3e34 || 1.4e13 || 210 || 530 km || The size is the kinetic diameter, leading to the mean free path, [[ https://en.wikipedia.org/wiki/Kinetic_diameter | Source ]] The number density altitude above does not consider particle mass, merely compares the estimated particles injected at GEO by a large SSPS constellation to number densities in the standard atmosphere at Low Earth Orbit altitudes. ISS orbits at 400 km altitude, masses about 1e6 kg, has a surface area of about 5000 m '''Given the short mean free path compared to the cyclotron radius, the following may not be true:''' The field essentially freezes the particles at the altitudes where they are ionized. For the LOX/LH2 plume, that can be anywhere that solar UV ionizes it, but for the plasma producing rockets, that is at the emission radius, very close to GEO. Compare those densities to 10 atoms per m³ for the hydrogen ions in the belts, ''vastly'' higher density. MoreLater === Thermal-Electric Thrust: Laser or Spark Ablation, Hydrogen Arcjet === Laser ablation propulsion might be problematic. Double pulse ablation collimates the plume surprisingly well, but the thermal-to-thrust-energy fraction is on the order of 20%, worse than a mediocre rocket expansion bell, and vastly worse than a vacuum expansion bell. Some fraction of the ablated material will come off in macroscopic globs; the erosion problem may be as bad as the small chunks of alumina spat out by the PAM solid motors used to circularize early comsats. Some of those globs were collected in LEO by the [[ https://en.wikipedia.org/wiki/Long_Duration_Exposure_Facility | Long Duration Exposure Facility ]] (LDEF) experiment. Until I see some careful empirical measurements of the entire plume emitted by a laser ablation thruster, I will consider laser ablation to be a somewhat improved and more controllable solid rocket, not a "clean" thrust system like an [[ http://www.adastrarocket.com/aarc/VASIMR | VASIMR ]] electric engine. MoreLater |
| Line 41: | Line 87: |
| Alternatives include arrival from ABOVE, construction in Highly Elliptical Earth Orbits (HEEO). HEEO arrival and apogee velocities are slower, delta V's are smaller, and the plumes are launched to escape. The slow relative arrival velocity permits semipassive vehicles and non-rocket capture systems (tailhooks! nets!) with the capture station restoring momentum using permanent high-ISP electric thrusters, perhaps using plentiful argon propellant frequently resupplied from the ground. Much more delta V is needed to raise perigee to GEO (again from a very high apogee with a relatively small Earth escape velocity). Arriving at GEO, more retrograde thrust is needed, but the propellant plume is launched forwards, faster than Earth escape velocity. | Alternatives include arrival from ABOVE, after construction in Highly Elliptical Earth Orbits (HEEO). HEEO arrival and apogee velocities are slower, delta V's are smaller, and the plumes are launched to escape. The slow relative arrival velocity permits semipassive vehicles and non-rocket capture systems (tailhooks! nets!) with the capture station restoring momentum using permanent high-ISP electric thrusters, perhaps using plentiful argon propellant frequently resupplied from the ground. Much more delta V is needed to raise perigee to GEO (again from a very high apogee with a relatively small Earth escape velocity). Arriving at GEO, more retrograde thrust is needed, but the propellant plume is launched forwards, faster than Earth escape velocity. |
| Line 47: | Line 93: |
| Laser ablation propulsion might be problematic. Double pulse ablation collimates the plume surprisingly well, but the thermal-to-thrust-energy fraction is on the order of 20%, worse than a mediocre rocket expansion bell, and vastly worse than a vacuum expansion bell. Some fraction of the ablated material will come off in macroscopic globs; the erosion problem may be as bad as the small chunks of alumina spat out by the PAM solid motors used to circularize early comsats. Some of those globs were collected in LEO by the [[ https://en.wikipedia.org/wiki/Long_Duration_Exposure_Facility | Long Duration Exposure Facility ]] (LDEF) experiment. Until I see some careful empirical measurements of the entire plume emitted by a laser ablation thruster, I will consider laser ablation to be a somewhat improved and more controllable solid rocket, not a "clean" thrust system like an [[ http://www.adastrarocket.com/aarc/VASIMR | VASIMR ]] electric engine. | == The Rotten Apple == ISP is '''''average''''' exhaust velocity. However, the propellant plume will have one or more temperatures, and temperature is velocity (squared, times 1.5 / k ). While the "average" velocity may not result in an orbiting plume, if the exhaust is not physically cooled (either by an expansion bell or by a narrow velocity acceleration process), then the statistics will be a Maxwellian Gaussian(?) in three dimensions. The "Rotten Apple" is a three dimensional projection of a sphere (in ''velocity space'') with an inner paraboloid cutout. It looks like a cored apple in three dimensions, except '''this''' apple is rotten; if it is a propellant plume, it will remain in orbit until it scatters or runs into something. Outside the sphere is escape velocity, except in the downwards projection of the paraboloid, which impacts the Earth. The horizontal center disk of the paraboloid (no vertical velocity, just sideways) is the apogee velocity of an elliptical orbit, with a perigee on the opposite side of the atmosphere ... and inside it. Some upward or downward velocity added to the horizontal velocity shifts the perigee angle. The ring at the top edge of the paraboloid represents an object (or a propellant plume atom) in a parabolic orbit, with apogee at the top of the atmosphere, 90 degrees from the physical position of the emitter in space. {{attachment:RottenApple4a.png | | width=400 }} . {{attachment:RottenApple4b.png | | width=400 }} |
| Line 50: | Line 106: |
SSPS is not the apotheosis of spacefaring human destiny. Global shipping rates in 2019 exceed ten billion tonnes per year (not including local travel); someday space traffic will far exceed that. 3 SSPS constellations ''per month'' cargo rates. If we hope to inhabit space for millions of years, and beyond, we must plan systems that leave no propellant plumes circling the Earth, and in the very long term, not even the Sun. Solve the earth orbit plume problem '''now''', and the solar orbit plume '''soon'''. |
SBSPplume
Some advocate sourcing all the world's energy with space-based solar power (SBSP), on the order of 30 Terawatts. They suggest space solar power satellite (SSPS) masses on the order of 4 kg / kW, or 0.004 kg per watt. That works out to 4e-3 kg/W * 3e13 W or 120e9 kg of SSPS mass delivered to Geostationary Earth Orbit ( GEO, 42164 km radius, 3075 m/s ). This does not include construction equipment or station-keeping fuel.
Modern comsats use noble-gas electric thrusters to climb to GEO. This is propellant-thrifty; however, this has driven up the price of xenon, so usage is shifting to krypton. There is not enough available high-Z noble gas (xenon, krypton) to raise the orbits of 120 million of tonnes of power satellite. There is plenty of argon, but that must be chilled below 87 Kelvin to store densely for the long spiral orbit to GEO.
The transfer orbit, and GEO injection velocity

So, consider liquid hydrogen + liquid oxygen (LH/LOX) chemical rockets, with typical 1:6 mass ratio (slightly fuel rich), producing a propellant plume of and H₂ and H. The mass ratio of water to total hydrogen ( H₂ plus H ), assuming complete combustion and no hydroxyl ( OH or HO ) or hydronium ( H₃O ), is 27:1. Ignore the hydrogen and presume the entire plume is H₂O.
Assuming a high expansion vacuum nozzle, the exhaust velocity of a LH/LOX engine might be as high as 4460 m/s.
Spacecraft typically launch to GEO from low earth orbit (LEO) via a geostationary transfer orbit (GTO). Presume that the GTO perigee starts from a 122 km equatorial altitude so that the GTO is an ellipse with perigee radius = 6500 km, apogee radius = 42164 km, semi-major axis 24332 km. The apogee velocity of the GTO ellipse is 1589 m/s. The GEO circularization delta V is (3075-1589) = 1486 m/s .
Presuming an exhaust velocity of 4460 m/s, and a delta V of 1486 m/s, the plume mass can be calculated using the Tsiolkovsky equation:
M_{plume} = M_{delivered} \times ( e^{ \Delta V / V_e } - 1 ) = 120e9 kg × ( exp( 1486 / 4460 ) - 1 ) = 120e9 kg × 0.395 = 47e9 kg.
The plume will be emitted in a retrograde direction from the vehicle as it accelerates from 1589 to 3075 m/s ; the plume velocity will range from (4460-1589) m/s to (4460-3075) m/s retrograde, or 2871 m/s to 1385 m/s.
What happens to the plume??
Even with a high expansion nozzle, the plume will be hot, with significant Maxwellian thermal velocity spread. Some species (molecules, atoms, ions) will travel more slowly than average, some faster. But let's ignore that to start with, and assume the gas molecules are all in retrograde elliptical orbits. What are the perigees of those orbits?
Well, to start with, we know a retrograde orbit with a velocity of -1589 m/s has a perigee of 122 km; slower species will descend to a lower altitude and fall into the atmosphere. Species with a retrograde velocity of -2871 m/s will have an perigee of 32600 km, and will remain above the atmosphere for a very long time. Species with a retrograde velocity of -1640 m/s will have a perigee above 600 km, and will remain in orbit for decades.
Lets consider the portion of the plume emitted between -1640 m/s and -2871 m/s to be in semi-permanent orbits, and the portion of the plume emitted between 1589 m/s and 1640 m/s to re-enter and stop being a problem. If the plume is -1640 m/s retrograde, the vehicle is travelling 4460-1640 = 2820 m/s prograde. So, the re-entering portion of the plume is the fraction emitted while the vehicle accelerates from 2820 to 3075 m/s, a delta V of 255 m/s. Let's use the Tsiolkovsky equation for that:
M_{entry} = M_{delivered} \times ( e^{ \Delta V / V_e } - 1 ) = 120e9 kg × ( exp( 255 / 4460 ) - 1 ) = 120e9 kg × 0.0588 = 7e9 kg.
So, the plume emitted into semi-permanent orbits is (47-7)e9 = 40e9 kg = 4e10 kg. Mostly water molecules, atomic weight 18, 3.35e25 molecules per kilogram, for a total of 1.3e36 molecules. Their orbital periods will range from 9 to 20 hours, so the average particle will return to orbit apogee every 50,000 seconds. Orbits with an apogee at GEO!
The flux rate through the entire GEO region is 2.6e31 molecules per second. If the molecules are in an average 50,000 second orbit (29334 km semimajor axis, ), their "dwell time" at a radius 10 km from apogee is 140 seconds, hence 0.28% of the molecules, or 3.6e33 molecules, are in a narrow "GEO torus" at any given time moving retrograde relative to the SSPS constellation at a (3075+2306) = 5381 m/s. The volume of that torus is . . . MoreLater (a better analysis involving dwell time)
Over those years, many (most?) of those species will collide with the ram (forward orbit facing) surfaces of thousands of kilo-hectare power satellites, at velocities up to 5946 m/s (3075 + (4460-1589)) slowing them and sputtering the ram surface. An H₂O molecule with a mass of 18 AMU (3e-26 kg) and a relative velocity of 7344 m/s has a kinetic energy of 5.3e-19 J or 3.3 electron volts. This can damage the power satellites.
For comparison, mono-atomic fringe-atmosphere oxygen at 500 km altitude above the 6371 km radius earth (6871 km) rotates with the earth at a velocity of 500 m/s. ISS (in a 54 degree inclined orbit) orbits at 7617 m/s. It encounters oxygen atoms while it crosses the equator at a relative velocity of (coincidentally!) 7344 m/s, with an impact energy of 3.1 eV. This slows ISS, requiring periodic thrust for reboost, and also sputters material off the ram surface of ISS, a known long term hazard.
Worse yet, a significant fraction of the plume atoms will have retrograde perigees at LEO, where there will be assets orbiting prograde. While a relatively small fraction of the plume emitted at GEO (with apogee at GEO) will (coincidentally) have perigees near important LEO assets, where they do, the velocity differences will be huge. Consider the International Space Station, ISS, in a circular LEO orbit with an "altitude" of 500 km, presumably a 6870 km radius orbit, inclined 54 degrees. Consider an H2O plume molecule in a 42164 by 6871 km orbit; it will have a perigee velocity close to 10 km/s. The closing velocity with ISS as it crosses the equator is 14.8 km/s, and the collision energy for an H2O molecule will be 20 eV, six times higher than the collision velocity for atomic oxygen.
If the plume is dense, it could be catastrophic to LEO objects. For objects in a prograde transfer orbit to GEO, the closing velocity will be 20 km/s, the collision energy will be 36 eV, huge, though hopefully objects in transfer orbits will only encounter this onslaught one time.
This is an "N squared" problem. Delivering 1500 tonnes of GEO comsat with a 500 tonnes of propellant plume is a 6 billion times smaller problem. The comsats are much denser than an SSPS, reducing the collision cross section even further. We have not encountered any major problems with our comsat fleet yet - unless plume collision erosion is responsible for a few unexplained losses ... ![]()
Ionization, Charged Particle Trapping on Field Lines
Accroding to this NASA "space math" exercise, the van Allen belts contain only two grams of protons (ionized hydrogen) at very high energy, a density averaging 1e-5/cm³ = 10/m³ in a 1e23 m³ volume out to 6 Re (I'm skeptical, but don't have a better source). GEO is 6.6 Re; lets assume the GEO insertion plume region is a spherical shell 200 km thick, a volume of 4.5e21 cubic meters.
Electric engines produce ions (like the Van Allen belts) so those can be trapped by field lines as well. The Earth dipole produces a field in the equatorial plane of B = B_0 ( Re / R )^3 where R is the radius, B_0 = 3.12e-5 Tesla and Re = 6.371e6 meters. At 6.6 Re, the field is 1.1e-7 Tesla. The cyclotron radius for a charged particle is r = m v / q B ; for an N amu (amu = 1.6e-27 kg, q = 1.6e-19 colombs ) particle at GEO the cyclotron radius r is ( 0.085 sec * N * v meters ), where v is "the" exhaust molecule velocity.
Here's a table of retrograde velocity and N for plausible exhaust species (minus the estimated "average" 2300 m/s prograde velocity of the GEO-orbit insertion rocket emitting them):
Cyclotron radius at 6.2 Re GEO "average" velocity |
Number |
|||||||||
Scenario |
species |
N |
size |
v |
Radius |
Mass |
Molecules |
Mean free |
Density |
|
|
|
|
pm |
km/s |
km |
kg |
total |
per m3 |
path μm |
Altitude |
LOX/LH2 |
H₂O |
18 |
270 |
2.2 |
3.4 |
4e10 |
1.4e36 |
3.1e14 |
12 |
338 km |
Hydrogen Arcjet |
H₂ |
2 |
290 |
8 |
1.4 |
1e10 |
3.1e36 |
6.9e14 |
5 |
297 km |
Teflon ablator |
CF |
31 |
xxx |
10 |
26 |
8e9 |
1.6e35 |
3.6e13 |
|
466 km |
Argon Helicon |
Ar |
40 |
340 |
20 |
68 |
4e9 |
6.3e34 |
1.4e13 |
210 |
530 km |
The size is the kinetic diameter, leading to the mean free path, Source
The number density altitude above does not consider particle mass, merely compares the estimated particles injected at GEO by a large SSPS constellation to number densities in the standard atmosphere at Low Earth Orbit altitudes. ISS orbits at 400 km altitude, masses about 1e6 kg, has a surface area of about 5000 m
Given the short mean free path compared to the cyclotron radius, the following may not be true:
The field essentially freezes the particles at the altitudes where they are ionized. For the LOX/LH2 plume, that can be anywhere that solar UV ionizes it, but for the plasma producing rockets, that is at the emission radius, very close to GEO. Compare those densities to 10 atoms per m³ for the hydrogen ions in the belts, vastly higher density.
Thermal-Electric Thrust: Laser or Spark Ablation, Hydrogen Arcjet
Laser ablation propulsion might be problematic. Double pulse ablation collimates the plume surprisingly well, but the thermal-to-thrust-energy fraction is on the order of 20%, worse than a mediocre rocket expansion bell, and vastly worse than a vacuum expansion bell. Some fraction of the ablated material will come off in macroscopic globs; the erosion problem may be as bad as the small chunks of alumina spat out by the PAM solid motors used to circularize early comsats. Some of those globs were collected in LEO by the Long Duration Exposure Facility (LDEF) experiment. Until I see some careful empirical measurements of the entire plume emitted by a laser ablation thruster, I will consider laser ablation to be a somewhat improved and more controllable solid rocket, not a "clean" thrust system like an VASIMR electric engine.
So ... don't do it that way.
Alternatives include arrival from ABOVE, after construction in Highly Elliptical Earth Orbits (HEEO). HEEO arrival and apogee velocities are slower, delta V's are smaller, and the plumes are launched to escape. The slow relative arrival velocity permits semipassive vehicles and non-rocket capture systems (tailhooks! nets!) with the capture station restoring momentum using permanent high-ISP electric thrusters, perhaps using plentiful argon propellant frequently resupplied from the ground. Much more delta V is needed to raise perigee to GEO (again from a very high apogee with a relatively small Earth escape velocity). Arriving at GEO, more retrograde thrust is needed, but the propellant plume is launched forwards, faster than Earth escape velocity.
Of course, higher ISP electric engines for a LEO to GEO spiral orbit will also launch their propellant plumes retrograde, much faster than escape. However, not all electric engines are created equal; if the bell expansion is small or absent, the plumes will have high thermal velocities, and a significant fraction of the plume species will go into permanent orbits; some with high apogees, meaning they could arrive at the ram surface of the SSPS with more than double GEO orbit velocity, nearlt as fast as the relative speed for atomic oxygen at the ram surface of GEO objects.
The fraction will be smaller ... this is good ... but it would be better to make it MUCH smaller with careful plume management.
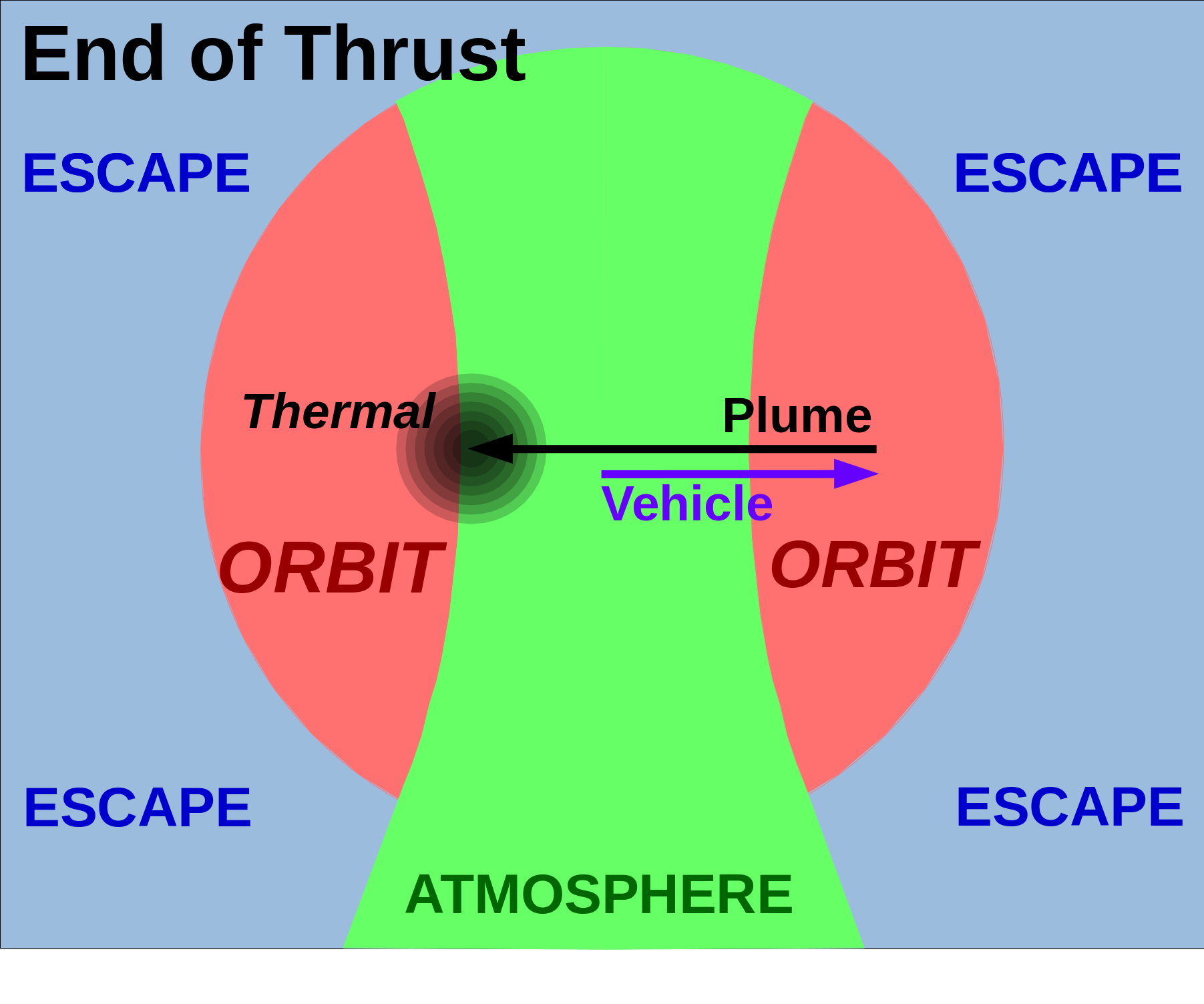
The Rotten Apple
ISP is average exhaust velocity. However, the propellant plume will have one or more temperatures, and temperature is velocity (squared, times 1.5 / k ). While the "average" velocity may not result in an orbiting plume, if the exhaust is not physically cooled (either by an expansion bell or by a narrow velocity acceleration process), then the statistics will be a Maxwellian Gaussian(?) in three dimensions.
The "Rotten Apple" is a three dimensional projection of a sphere (in velocity space) with an inner paraboloid cutout. It looks like a cored apple in three dimensions, except this apple is rotten; if it is a propellant plume, it will remain in orbit until it scatters or runs into something.
Outside the sphere is escape velocity, except in the downwards projection of the paraboloid, which impacts the Earth. The horizontal center disk of the paraboloid (no vertical velocity, just sideways) is the apogee velocity of an elliptical orbit, with a perigee on the opposite side of the atmosphere ... and inside it. Some upward or downward velocity added to the horizontal velocity shifts the perigee angle. The ring at the top edge of the paraboloid represents an object (or a propellant plume atom) in a parabolic orbit, with apogee at the top of the atmosphere, 90 degrees from the physical position of the emitter in space.
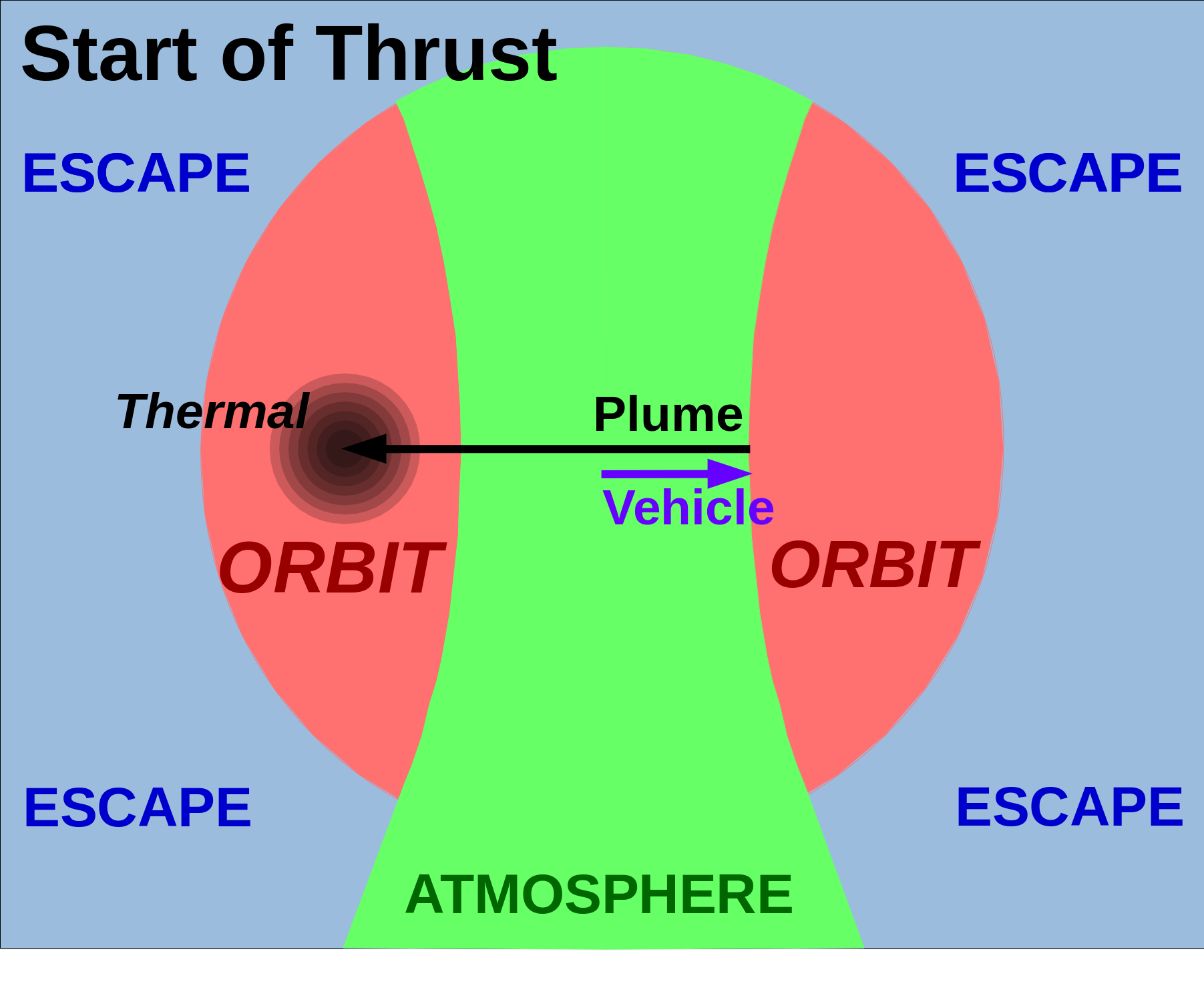 .
. 
Think Ahead! Design as if the far future MATTERS!
SSPS is not the apotheosis of spacefaring human destiny. Global shipping rates in 2019 exceed ten billion tonnes per year (not including local travel); someday space traffic will far exceed that. 3 SSPS constellations per month cargo rates. If we hope to inhabit space for millions of years, and beyond, we must plan systems that leave no propellant plumes circling the Earth, and in the very long term, not even the Sun. Solve the earth orbit plume problem now, and the solar orbit plume soon.
