|
Size: 2244
Comment:
|
Size: 14192
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| = Mountain Myths about Space Launch = | #format jsmath = A Mountain of Myths about Space Launch = |
| Line 3: | Line 4: |
| || Altitude || Density || Year || Record || || km || atmos. || || || || 0.0 || 1.00 || || Standard density 1.225 kg/m³, varies || || 8.848 || 4.07e-1 || 1953 || Everest, Highest Mountain || || 37.65 || 4.62e-3 || 1977 || Highest Airbreathing Manned Aircraft || || 41.4 || 2.66e-3 || 2014 || Highest Altitude Manned Balloon || || 53.0 || 5.86e-4 || 2002 || Highest Altitude Unmanned Balloon || || 99.0 || 5.49e-7 || || "in" the atmosphere, national airspace || || 100.0 || 4.58e-7 || || Legal Boundary of Space || || 101.0 || 3.83e-7 || || "out of" the atmosphere, international || || 160.0 || 1.01e-9 || || rapidly decaying single orbit || || 200.0 || 2.1e-10 || || practical short term orbit || || 400.0 || 2.3e-12 || || International Space Station || orbit decays 2 kilometers per month || |
|| Altitude || Density || Year || Record || || km || atmos. || || || || 0.0 || 1.00 || || Standard density 1.225 kg/m³, varies || || 8.848 || 4.07e-1 || 1953 || Everest, Highest Mountain || || 37.65 || 4.62e-3 || 1977 || Highest Airbreathing Manned Aircraft || || 41.4 || 2.66e-3 || 2014 || Highest Altitude Manned Balloon || || 53.0 || 5.86e-4 || 2002 || Highest Altitude Unmanned Balloon || || 99.0 || 5.49e-7 || || "in" the atmosphere, national airspace || || 100.0 || 4.58e-7 || || Legal Boundary of Space || || 101.0 || 3.83e-7 || || "out of" the atmosphere, international || || 160.0 || 1.01e-9 || || rapidly decaying single orbit || || 200.0 || 2.1e-10 || || practical short term orbit - days? Depends on area and density || || 400.0 || 2.3e-12 || || International Space Station - orbit decays 2 kilometers per month || |
| Line 17: | Line 18: |
| Space is high vacuum. Zero lift for wings or balloons. The legal boundary of 100 km is convenient but entirely arbitrary; it is twice as high as any atmospheric vehicle can fly or float, and half as high as any practical satellite can orbit. Tourist suborbitals to 100 km (like [[ https://en.wikipedia.org/wiki/SpaceShipOne | SpaceShipOne ]] ) are not practical spacecraft, merely dangerous and ostentatious displays of wealth, like climbing Mount Everest without the exercise. | Space is high vacuum. Zero lift for wings or balloons. The legal boundary of 100 km (the [[ https://en.wikipedia.org/wiki/K%C3%A1rm%C3%A1n_line | Kármán line ]] ) is convenient but entirely arbitrary; it is twice as high as any atmospheric vehicle can fly or float, and half as high as any practical satellite can orbit. Tourist suborbitals to 100 km (like [[ https://en.wikipedia.org/wiki/SpaceShipOne | SpaceShipOne ]] ) are not practical spacecraft, merely dangerous and ostentatious entertainment, somewhat like [[ http://www.mountainguides.com/photos/everest-south/side-summit03-gary-dave.jpg | climbing Mount Everest ]] but without the strenuous exercise or rigorous accomplishment. |
| Line 21: | Line 22: |
| If you were suddenly transported to 400 km altitude and dropped from there, you would not orbit the Earth, you would fall down, your vertical speed increasing rapidly. | === A 400 kilometer drop from Space Station altitude, zero orbital velocity === If you were suddenly transported to 400 km altitude (in a space suit) and dropped from there, you would not orbit the Earth. You would fall down, your vertical speed increasing rapidly. After [[attachment:Fall400km.ods | 260 seconds]], you would plunge through the 100 km altitude Kármán line at 2330 meters per second, [[ http://launchloop.com/Atmosphere | 8 times the speed of sound ]] at that altitude, but you would notice nothing, a 0.3 Pascal pressure force added to the 100 kPa (100,000 Pascal( air pressure in your suit. Things get frisky during your final 40 second plunge deep into the atmosphere, approaching a terminal velocity of 2700 m/s. At 7.1 kilometers altitude (higher than all mountain peaks in the Western Hemisphere), the air density is about half of sea level. However, the wind pressure beneath you is 40 times air pressure, about 400 tonnes per square meter; you would be smashed to jelly, though you would not burn up like a (vastly faster) small meteor. . Actually not, you slam on the brakes at a higher altitude. You will stop accelerating and slow down when the drag pressure equals gravity. If your effective drag area is 1 square meter and you and your suit weigh 100 kilograms, then 1000 Pascals of pressure will start slowing you down at an atmospheric density around 170 ppm of surface, around 60 kilometers up. Air density (and drag pressure) doubles every two seconds, so within 10 more seconds of downward plunge, your suit will be ripped off by turbulence, and you will be crushed by gee forces. Meteors arrive at 15 to 30 thousand meters per second. Orbital velocity is around 8000 meters per second, and air drag force is proportional to velocity squared. So, entering at orbital velocity is about 9 times the drag force of a 400 kilometer plunge, and vastly more than encountered by !SpaceShipOne, though 4 to 14 times lower than a meteor. Meteors (and reentering spacecraft) slow down higher in the atmosphere; the smallest meteorites may burn up, but most hit the ground at bullet speed, with a charred surface and a frozen (by deep space) center. As we tragically learned in the catastrophic entry of [[ https://en.wikipedia.org/wiki/Space_Shuttle_Columbia_disaster | Columbia ]], damaged vehicles are ripped to shreds in the middle atmosphere (70 km for Columbia, air density 70 ppm of surface density), but most fragments impact the ground intact. . Launch Loop (2017 design) vehicles reach orbital velocity at 100 km altitude, 0.5 ppm of surface density, so the drag pressure is 140 times lower than 70 km shuttle entry altitude. Passenger vehicles may fail to enter orbit (they require an additional small rocket burn half an orbit later, to circularize the orbit at destination altitude), and must be capable of reentry, but these will be not be fragile winged reentry. Instead, ablative heat-shield slowdown reentries, followed and parachute splashdown in the ocean, perhaps 20 degrees west of the launch loop for vehicles intended for low earth orbit destinations, and 100 degrees west for GEO-bound vehicles. '''Takeaway lesson:''' Reentry slowdown occurs 50 to 80 kilometers above the surface, and the slowdown forces double every 5 kilometers deeper into the atmosphere. === Mountains === 7000 meter mountains seem impressive to 2 meter human beings, but they are trivial bumps compared to the depth of the atmosphere or the 12,740,000 meter diameter of the Earth. Scaled to the diameter of a 57mm billiard ball, these mountains would be 30 micrometers high; P500 fine-grit polishing-grade sandpaper. Indeed, a 100 kilometer joyride to the "edge of space" is only half a millimeter compared to the billiard ball - beard stubble. The excuse for space-launch schemes involving mountains is that the air is thinner at the top, somewhat less drag. But remember that the space shuttle Columbia was torn apart by aerodynamic forces at 70 kilometers altitude, where air density is 70 ppm of surface density. The air at the top of Mount Everest is 400,000 ppm of surface density, 6,000 times higher. Columbia was slowing from orbit, reentering, not trying to punch through the atmosphere with enough velocity remaining to go into orbit. 400 km altitude low earth orbits follow the curve of the earth, the equivalent of 2 millimeters above the surface a the billiard ball. Practically speaking, they are parallel to the surface. Mountains point diagonally upward; as we will see, the worst combination of two diametrically opposed problems. . On a round airless body like the Moon, an orbit can skim relatively close to the surface; the Apollo 11 command module orbited 62 kilometers above the Moon, and could have orbited down to 15 km ([citation needed], the [[Apsides | perilune]] for the initial LM descent orbit) for an emergency rendezvous with a disabled lunar module. For comparison, the cruise altitude of the Concorde SST was 17 to 18 km, and the U2 flew at 21 km altitude. Earth transfer orbits in vacuum, like the ascent of the lunar module, are zero-gee ellipses; at the [[Apsides | perigee and apogee]] portions of their orbits, they are also parallel to the surface of the body they orbit. They oscillate radially, smoothly, and their radial distance approximates a sine wave if the difference between perigee and apogee is relatively small. If a mountaintop launch is into an elliptical transfer orbit (say, to LEO) that transfer orbit is '''parallel''' to the Earth's surface, and travels thousands of kilometers through very thick atmosphere. Much thicker atmosphere (6000 times denser) than spacecraft of average density use to '''slow down and reenter'''. Objects in thick atmosphere slow down '''extremely fast'''. "Ah", I can hear you object, "of course we won't launch parallel to the surface, we will launch up the side of the mountain, going up through the atmosphere at a '''steep angle'''). Indeed, that reduces the time spent experiencing superhigh drag, so less velocity must be added up front to lose in the first seconds after release. But the path length is still shallow and long. I don't know about the mountains of your imagination, but the tall mountains that I know about are rarely steeper than 40 degrees from base to peak. From the Khumbu ice fall to the peak of Everest is a 28 degree slope, 2.8 kilometers vertical rise in a 5.1 kilometer horizontal distance. A deep tunnel dug from Everest base camp in the west to the peak of Everest in the east would cover about 7.6 kilometers of horizontal distance, and 3.5 kilometers vertical distance, perhaps 8500 meters of curved then flat sloped acceleration track to stay on or in the mountain. {{attachment:Everestlaunch.png| |width=600}} . ~-modified from National Geographic map, found online. Will remove if requested.-~ Good luck [[ https://en.wikipedia.org/wiki/Gotthard_Base_Tunnel | digging that tunnel]], and [[ https://en.wikipedia.org/wiki/China_Village_Electrification_Program | connecting gigawatts of power lines ]] to it. A vehicle accelerating in a vacuum tunnel from 0 to 8000 meters per second over 8500 meters distance must accelerate at $ a = v^2 / 2 d $ = 8000² / 2 * 8500 = 3765 m/s², or 385 gees. You will spill your drink, as you are '''smashed into goo''' of the same consistency. If this is a 5000 kilogram vehicle, near the exit it will require a power level of $ P = m a v $ = 5000 * 3765 * 8000 = 150 gigawatts, 9% of all of China's 1650 gigawatts of electric generation for a few seconds. I exaggerate - the power is pulsed, and will come from some gynormous energy storage system and be distributed through many [[MassDriver | gynormous switches and power cables]]. Which we must build and maintain deep in the frozen mountains at the end of yak trails. Right. When the vehicle containing your liqufied remains leaves the vacuum tunnel, it will slam into a wall of 0.45 kg/m³ air at an altitude of 8.5 km (below cruise altitude for most jet passenger aircraft). Assuming a 1 square meter vehicle cross section times drag coefficient, the drag force is 0.45 * 8000² = 28.8 !MegaNewtons, which will slow down the vehicle by 5760 m/s², or about '''590 gees'''. Tough luck - in the remaining atmosphere, you will '''lose all your velocity''' and smack into the next mountain to the west of Everest. Even if we send the atmosphere off to the cleaners to scrub out all US and Chinese electric generation exhaust, our troubles are not over. You are leaving the Earth at a 30 degree angle, not horizontal to the surface; you will be in an ellipse that intersects the Earth. your velocity is 8000 meters per second, but your horizontal velocity is "only" 8000 cos( 30⁰ ) = 6930 m/s Using equations from [[ http://server-sky.com/NearCircularOrbit | this Server Sky page ]], we learn that the semimajor axis for a launch at circular orbit velocity but elevated above the surface by an angle of 30⁰ results in an eccentricity e = sin( 30⁰ ) = 0.5, to the perigee is (1-e) a = 3193 km, and the apogee is (1+e) a = 9579 km. This orbit will arc above the earth for an apogee about 90⁰ to the east, then slam into the Earth's surface about 180⁰ to the east, on the far side of the earth. With a large additional delta V at apogee, the perigee can be raised above the Earth, but sadly, your apogee rocket will get smashed to goo by the launch acceleration. Oh - and how are you going to do that accelerator? [[ https://en.wikipedia.org/wiki/Railgun#U.S._Navy_tests | Railguns are ablative ]], and do more damage to the rails and power source than an ablative projectile will do to the target. [[ http://launchloop.com/ZeroToEighty | Switched coilguns ]] ( later renamed [[ https://en.wikipedia.org/wiki/Mass_Driver | "mass drivers" ]] ) require vastly expensive high speed electronic switching to route impulse power from some storage source to create a fast moving magnetic field gradient that drives the projectile. The conductive projectile develops high currents to resist the field, which are proportional to the force; huge forces mean enormous ohmic heating, which can melt or even vaporize the conductor. ---- === To recap === * Mountains aren't nearly high enough to affect launch aerodynamics and reduce drag to human-tolerable levels * Mountains are way too short for zero-to-orbital velocity change at human-tolerable acceleration * Coilguns AKA mass drivers require way too much electrical power in a very short time, and the switches are way too expensive * Railguns ditto, and the rails wear out too fast People keep writing about this nonsense, as if aerodynamics and orbital geometry don't matter. That is why I looked for alternatives in the late 1970's and early 80's and after many failed attempts came up with the launch loop. Which may also be a failed attempt, but I spent 40 years, not 40 minutes, trying to find fatal show-stoppers, instead finding many fascinating solutions for problems that can be profitably applied to many other global problems. I don't pretend to have all the answers for the Launch Loop, either, but there are no freshman physics show-stoppers, and I am still finding better and better answers. While many difficult advanced-degree problems remained to be solved, they are, as my late friend Robert Forward said, "mere engineering details". Increasing safety and efficiency and productivity, while reducing cost. |
A Mountain of Myths about Space Launch
Altitude |
Density |
Year |
Record |
km |
atmos. |
|
|
0.0 |
1.00 |
|
Standard density 1.225 kg/m³, varies |
8.848 |
4.07e-1 |
1953 |
Everest, Highest Mountain |
37.65 |
4.62e-3 |
1977 |
Highest Airbreathing Manned Aircraft |
41.4 |
2.66e-3 |
2014 |
Highest Altitude Manned Balloon |
53.0 |
5.86e-4 |
2002 |
Highest Altitude Unmanned Balloon |
99.0 |
5.49e-7 |
|
"in" the atmosphere, national airspace |
100.0 |
4.58e-7 |
|
Legal Boundary of Space |
101.0 |
3.83e-7 |
|
"out of" the atmosphere, international |
160.0 |
1.01e-9 |
|
rapidly decaying single orbit |
200.0 |
2.1e-10 |
|
practical short term orbit - days? Depends on area and density |
400.0 |
2.3e-12 |
|
International Space Station - orbit decays 2 kilometers per month |
Space is high vacuum. Zero lift for wings or balloons. The legal boundary of 100 km (the Kármán line ) is convenient but entirely arbitrary; it is twice as high as any atmospheric vehicle can fly or float, and half as high as any practical satellite can orbit. Tourist suborbitals to 100 km (like SpaceShipOne ) are not practical spacecraft, merely dangerous and ostentatious entertainment, somewhat like climbing Mount Everest but without the strenuous exercise or rigorous accomplishment.
Real space is orbit, and the lowest practical orbit is 200 km. Even that is far too low for a large, high-drag object like ISS, which requires frequent reboost to compensate for air drag, even though the air is 2 parts per trillion of the density at sea level. That is a difficult number to grasp - a volume of "ISS vacuum" as big as AT&T Stadium in Texas (104 million cubic feet, 3 million cubic meters) would fit in 7 cubic centimeters, half a tablespoon, if compressed to sea level density.
A 400 kilometer drop from Space Station altitude, zero orbital velocity
If you were suddenly transported to 400 km altitude (in a space suit) and dropped from there, you would not orbit the Earth. You would fall down, your vertical speed increasing rapidly. After 260 seconds, you would plunge through the 100 km altitude Kármán line at 2330 meters per second, 8 times the speed of sound at that altitude, but you would notice nothing, a 0.3 Pascal pressure force added to the 100 kPa (100,000 Pascal( air pressure in your suit.
Things get frisky during your final 40 second plunge deep into the atmosphere, approaching a terminal velocity of 2700 m/s. At 7.1 kilometers altitude (higher than all mountain peaks in the Western Hemisphere), the air density is about half of sea level. However, the wind pressure beneath you is 40 times air pressure, about 400 tonnes per square meter; you would be smashed to jelly, though you would not burn up like a (vastly faster) small meteor.
- Actually not, you slam on the brakes at a higher altitude. You will stop accelerating and slow down when the drag pressure equals gravity. If your effective drag area is 1 square meter and you and your suit weigh 100 kilograms, then 1000 Pascals of pressure will start slowing you down at an atmospheric density around 170 ppm of surface, around 60 kilometers up. Air density (and drag pressure) doubles every two seconds, so within 10 more seconds of downward plunge, your suit will be ripped off by turbulence, and you will be crushed by gee forces.
Meteors arrive at 15 to 30 thousand meters per second. Orbital velocity is around 8000 meters per second, and air drag force is proportional to velocity squared. So, entering at orbital velocity is about 9 times the drag force of a 400 kilometer plunge, and vastly more than encountered by SpaceShipOne, though 4 to 14 times lower than a meteor. Meteors (and reentering spacecraft) slow down higher in the atmosphere; the smallest meteorites may burn up, but most hit the ground at bullet speed, with a charred surface and a frozen (by deep space) center. As we tragically learned in the catastrophic entry of Columbia, damaged vehicles are ripped to shreds in the middle atmosphere (70 km for Columbia, air density 70 ppm of surface density), but most fragments impact the ground intact.
- Launch Loop (2017 design) vehicles reach orbital velocity at 100 km altitude, 0.5 ppm of surface density, so the drag pressure is 140 times lower than 70 km shuttle entry altitude. Passenger vehicles may fail to enter orbit (they require an additional small rocket burn half an orbit later, to circularize the orbit at destination altitude), and must be capable of reentry, but these will be not be fragile winged reentry. Instead, ablative heat-shield slowdown reentries, followed and parachute splashdown in the ocean, perhaps 20 degrees west of the launch loop for vehicles intended for low earth orbit destinations, and 100 degrees west for GEO-bound vehicles.
Takeaway lesson: Reentry slowdown occurs 50 to 80 kilometers above the surface, and the slowdown forces double every 5 kilometers deeper into the atmosphere.
Mountains
7000 meter mountains seem impressive to 2 meter human beings, but they are trivial bumps compared to the depth of the atmosphere or the 12,740,000 meter diameter of the Earth. Scaled to the diameter of a 57mm billiard ball, these mountains would be 30 micrometers high; P500 fine-grit polishing-grade sandpaper. Indeed, a 100 kilometer joyride to the "edge of space" is only half a millimeter compared to the billiard ball - beard stubble.
The excuse for space-launch schemes involving mountains is that the air is thinner at the top, somewhat less drag. But remember that the space shuttle Columbia was torn apart by aerodynamic forces at 70 kilometers altitude, where air density is 70 ppm of surface density. The air at the top of Mount Everest is 400,000 ppm of surface density, 6,000 times higher. Columbia was slowing from orbit, reentering, not trying to punch through the atmosphere with enough velocity remaining to go into orbit.
400 km altitude low earth orbits follow the curve of the earth, the equivalent of 2 millimeters above the surface a the billiard ball. Practically speaking, they are parallel to the surface. Mountains point diagonally upward; as we will see, the worst combination of two diametrically opposed problems.
On a round airless body like the Moon, an orbit can skim relatively close to the surface; the Apollo 11 command module orbited 62 kilometers above the Moon, and could have orbited down to 15 km ([citation needed], the perilune for the initial LM descent orbit) for an emergency rendezvous with a disabled lunar module. For comparison, the cruise altitude of the Concorde SST was 17 to 18 km, and the U2 flew at 21 km altitude.
Earth transfer orbits in vacuum, like the ascent of the lunar module, are zero-gee ellipses; at the perigee and apogee portions of their orbits, they are also parallel to the surface of the body they orbit. They oscillate radially, smoothly, and their radial distance approximates a sine wave if the difference between perigee and apogee is relatively small.
If a mountaintop launch is into an elliptical transfer orbit (say, to LEO) that transfer orbit is parallel to the Earth's surface, and travels thousands of kilometers through very thick atmosphere. Much thicker atmosphere (6000 times denser) than spacecraft of average density use to slow down and reenter. Objects in thick atmosphere slow down extremely fast.
"Ah", I can hear you object, "of course we won't launch parallel to the surface, we will launch up the side of the mountain, going up through the atmosphere at a steep angle). Indeed, that reduces the time spent experiencing superhigh drag, so less velocity must be added up front to lose in the first seconds after release. But the path length is still shallow and long.
I don't know about the mountains of your imagination, but the tall mountains that I know about are rarely steeper than 40 degrees from base to peak. From the Khumbu ice fall to the peak of Everest is a 28 degree slope, 2.8 kilometers vertical rise in a 5.1 kilometer horizontal distance. A deep tunnel dug from Everest base camp in the west to the peak of Everest in the east would cover about 7.6 kilometers of horizontal distance, and 3.5 kilometers vertical distance, perhaps 8500 meters of curved then flat sloped acceleration track to stay on or in the mountain.
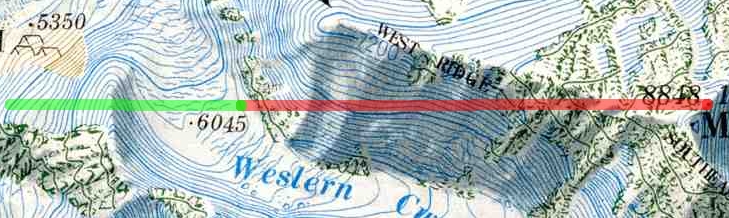
modified from National Geographic map, found online. Will remove if requested.
Good luck digging that tunnel, and connecting gigawatts of power lines to it.
A vehicle accelerating in a vacuum tunnel from 0 to 8000 meters per second over 8500 meters distance must accelerate at a = v^2 / 2 d = 8000² / 2 * 8500 = 3765 m/s², or 385 gees. You will spill your drink, as you are smashed into goo of the same consistency. If this is a 5000 kilogram vehicle, near the exit it will require a power level of P = m a v = 5000 * 3765 * 8000 = 150 gigawatts, 9% of all of China's 1650 gigawatts of electric generation for a few seconds.
I exaggerate - the power is pulsed, and will come from some gynormous energy storage system and be distributed through many gynormous switches and power cables. Which we must build and maintain deep in the frozen mountains at the end of yak trails. Right.
When the vehicle containing your liqufied remains leaves the vacuum tunnel, it will slam into a wall of 0.45 kg/m³ air at an altitude of 8.5 km (below cruise altitude for most jet passenger aircraft). Assuming a 1 square meter vehicle cross section times drag coefficient, the drag force is 0.45 * 8000² = 28.8 MegaNewtons, which will slow down the vehicle by 5760 m/s², or about 590 gees. Tough luck - in the remaining atmosphere, you will lose all your velocity and smack into the next mountain to the west of Everest.
Even if we send the atmosphere off to the cleaners to scrub out all US and Chinese electric generation exhaust, our troubles are not over. You are leaving the Earth at a 30 degree angle, not horizontal to the surface; you will be in an ellipse that intersects the Earth. your velocity is 8000 meters per second, but your horizontal velocity is "only" 8000 cos( 30⁰ ) = 6930 m/s Using equations from this Server Sky page, we learn that the semimajor axis for a launch at circular orbit velocity but elevated above the surface by an angle of 30⁰ results in an eccentricity e = sin( 30⁰ ) = 0.5, to the perigee is (1-e) a = 3193 km, and the apogee is (1+e) a = 9579 km. This orbit will arc above the earth for an apogee about 90⁰ to the east, then slam into the Earth's surface about 180⁰ to the east, on the far side of the earth.
With a large additional delta V at apogee, the perigee can be raised above the Earth, but sadly, your apogee rocket will get smashed to goo by the launch acceleration.
Oh - and how are you going to do that accelerator? Railguns are ablative, and do more damage to the rails and power source than an ablative projectile will do to the target.
Switched coilguns ( later renamed "mass drivers" ) require vastly expensive high speed electronic switching to route impulse power from some storage source to create a fast moving magnetic field gradient that drives the projectile. The conductive projectile develops high currents to resist the field, which are proportional to the force; huge forces mean enormous ohmic heating, which can melt or even vaporize the conductor.
To recap
- Mountains aren't nearly high enough to affect launch aerodynamics and reduce drag to human-tolerable levels
- Mountains are way too short for zero-to-orbital velocity change at human-tolerable acceleration
- Coilguns AKA mass drivers require way too much electrical power in a very short time, and the switches are way too expensive
- Railguns ditto, and the rails wear out too fast
People keep writing about this nonsense, as if aerodynamics and orbital geometry don't matter. That is why I looked for alternatives in the late 1970's and early 80's and after many failed attempts came up with the launch loop. Which may also be a failed attempt, but I spent 40 years, not 40 minutes, trying to find fatal show-stoppers, instead finding many fascinating solutions for problems that can be profitably applied to many other global problems.
I don't pretend to have all the answers for the Launch Loop, either, but there are no freshman physics show-stoppers, and I am still finding better and better answers. While many difficult advanced-degree problems remained to be solved, they are, as my late friend Robert Forward said, "mere engineering details". Increasing safety and efficiency and productivity, while reducing cost.
