|
Size: 20600
Comment:
|
Size: 20647
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 16: | Line 16: |
| || [[ #41 | Transfer orbit 1 ]] ||<)> 69057 ||<)> 39500 ||<)> 75950 ||<)> 3.644 ||<)> 1.894 ||<)> 8° S ||<)> 0.873 || || [[ #46 | Transfer orbit 2 ]] ||<)> 21610 ||<)> 39500 ||<)> 45008 ||<)> 3.279 ||<)> 2.877 ||<)> 8° S ||<)> 0.366 || || [[ #51 | circular GEO ]] ||<)> years ||<)> 42164 ||<)> 42164 ||<)> 3.075 ||<)> 3.075 ||<)> 0° ||<)> 0.906 || |
|| [[ #41 | Transfer orbit 1 ]] ||<)> 69057 ||<)> 39500 ||<)> 75950 ||<)> 3.644 ||<)> 1.894 ||<)> 8° S ||<)> 0.874 || || [[ #46 | Transfer orbit 2 ]] ||<)> 21610 ||<)> 39500 ||<)> 45213 ||<)> 3.282 ||<)> 2.867 ||<)> 8° S ||<)> 0.366 || || [[ #51 | circular GEO ]] ||<)> years ||<)> 42164 ||<)> 42164 ||<)> 3.075 ||<)> 3.075 ||<)> 0° ||<)> 0.907 || |
| Line 20: | Line 20: |
| Line 124: | Line 123: |
| Transfer orbit 2 is an 8 degree inclined and slightly elliptical orbit that crosses geosynchronous orbit close to its semilatus rectum. A 366 m/s retrograde thrust at 39500 kilometer perigee drops apogee down to 45008 kilometers. A vehicle with a high ISP rocket typically spends a bit more than six hours making one quarter of an orbit from perigee to the final thrust. As before, if a high ISP electric rocket is used, this may take many orbits. | Transfer orbit 2 is an 8 degree inclined and slightly elliptical orbit that crosses geosynchronous orbit with a radius of 42164 km = $ a ( 1 - e^2 ) = 2 ( r_p r_a ) / ( r_p + r_a ) $ . A 366 m/s retrograde thrust at 39500 kilometer perigee drops apogee down to 45213 kilometers. A vehicle with a high ISP rocket typically spends a bit more than six hours making one quarter of an orbit from perigee to the final thrust. As before, if a high ISP electric rocket is used, this may take many orbits. |
High Apogee Construction Orbit with a Launch Loop
The goal for this example will be assembling large microwave-transmitting space solar power satellites (SSPS) using thousands of 5 tonne vehicles from a minimum-scale 10,000 tonne/day launch loop. The same process can be used to assemble smaller 183 GHz millimeter wave SSPS, lunar landers, deep space probes, or very large vehicles for interplanetary missions.
Launch loops can scale up to enormous size (and cost), but don't scale much smaller than 5 tonne vehicles at 3 gees, a consequence of winds in the atmosphere they rise through.
Mission summary, 1 stellar day construction orbit . . spreadsheet |
|||||||
Mission Segment |
duration |
perigee |
apogee |
vp |
va |
perigee |
entry Δv |
|
seconds |
km |
km |
km/s |
km/s |
inclination |
km/s |
340 |
6428 |
6458 |
0.471 |
10.667 |
8° S |
10.196 |
|
41657 |
6458 |
75950 |
10.667 |
0.906 |
8° S |
0.000 |
|
86164*N |
8378 |
75950 |
9.258 |
1.021 |
8° S |
0.114 |
|
69057 |
39500 |
75950 |
3.644 |
1.894 |
8° S |
0.874 |
|
21610 |
39500 |
45213 |
3.282 |
2.867 |
8° S |
0.366 |
|
years |
42164 |
42164 |
3.075 |
3.075 |
0° |
0.907 |
|
days |
8378 |
384400 |
9.650 |
0.210 |
varies |
0.392 |
|
The very low cost of loop launch into high apogee orbits enables the assembly of large spacecraft and structures from 5 tonne components. If the apogee is very high, then a small Δv at apogee can raise the perigee of the orbit well above relatively crowded LEO orbits. For this discussion, assume 2000 km perigee altitude is adequate, and a 1 stellar day delivery cycle, hence a 84328 km -(6378+2000 km) = 75950 km apogee.
Launch from the Loop
The launch loop will be located south of the equator for gentle and steady weather. 8 degrees south latitude, east of French Polynesia and west of South America may be the best region for launch loop deployments.
The earth rotates once per stellar day (relative to the fixed stars) every 86164.0989 seconds. The launch loop rotates under the perigee of an orbit at exactly this rate. In order to add another component to an orbiting assembly, it should be launched as the assembly is near perigee, overhead, timed within milliseconds. This can only happen if perigee is synchronized with the Earth's stellar day rotation, with corrections for Lunar tidal effects and the equatorial bulge.
An additional complication is apsidal precession. As a highly elliptical orbit passes near the oblate earth, the orbit will turn a little more than the classic case; as a consequence, the apogee and the next perigee will be a few seconds eastward. This will lengthen the orbit somewhat.
A fully-powered minimum launch loop can launch a 5 tonne vehicle every 45 seconds; that is 1920 vehicles per solar day, 5 less than that per stellar day. That can feed thousands of construction orbits and thousands of projects.
While it may be possible to launch groups of vehicles more closely timed than 45 seconds, each vehicle adds tension and deflection to the track. The tension is maximum at low speed near west station. Tight grouping will increase stress over the entire track, and reduce total throughput. In 45 seconds, the earth turns 0.19 degrees, and apogee "turns" 780 kilometers. Since higher orbits are slower orbits, it is possible to send a string of vehicles to a series of cascaded higher orbits that intersect the construction orbit at somewhat higher velocities, and use somewhat more apogee delta V to inject them into the same construction orbit, permitting higher total throughput during a multi-month construction program.
I will presume we can launch 20 vehicles spaced over a 15 minute range ( +/- 7.5 minutes ) per launch loop, 20 per stellar day. There should be at least three launch loops, providing redundancy in case of failure. If two operate on the same latitude and different longitudes, that can double the vehicle delivery rate per construction orbit. So, with enough power supply, two loops can deliver 200 tonnes per day to each of 96 construction orbits, about 10 million tonnes per year if all three loops operate at continual maximum power. More loops can be added, and they can be scaled MUCH larger if they are reliable and well defended.
Because of the equatorial bulge, perigee will precess westward by a few seconds per day, and the construction orbit and launch time should be lengthened to match; better orbit designers than I will compute the exact amount of precession and adjust the numbers presented here. The slightly shorter "days" used by launch and construction crews will be inconvenient in a 24.0 hour world. Multi-thousand tonne sub-structures may require more than year to assemble, and be passed between "red", "green", and "blue" teams on the ground. The substructures can be assembled into megatonne-scale structures in GEO, synchronized 24.0 hour ground team schedules and independent of launch loop scheduling.
An 80,000 tonne space solar power satellite might be assembled in GEO from 80 large subcomponents, 1000 tonnes each. Each subcomponent would be assembled from 250 five tonne loop launches (estimated four tonnes of payload and one tonne of propellant and thrust stage) from two loops over 4 months. Two loops at 75 percent capacity can launch 2000 of these 1000 tonne components per year.
Ballistic Trajectory from Loop Launch to 75950 km
Leaving the loop, vehicles will climb out through the upper atmosphere and encounter significant drag; they will need a sharp hypersonic nose cone with a heat resistant ablative spherical nose cap. However, the dynamic pressure and gee forces will be small, permitting the use of low-cost materials. An amusing possibility is "nanowood" 1,2 wood from trees that has been treated to remove most of the "live" material and leave only strong structural cellulose. As strong as ordinary wood, less dense and more insulating than styrofoam.
Should the apogee insertion rocket fail, cargo vehicles will re-enter somewhere to the west of the loop, probably disintegrating in the lower atmosphere if they are not equipped with heat shields and parachutes. Of course, passenger vehicles must be capable of safely re-entering, making them much more expensive than cargo vehicles. Vehicles will also briefly pass through the center of the van Allen radiation belts, but if they are launched into a high orbit at high speed, they will pass through the belts relatively rapidly.
Passengers will get a one-time radiation dose exceeding that of the Apollo astronauts, because launch towards a 6458x75950 km construction orbit from 8 degrees south passes them briefly through the equatorial plane at 24150 km altitude, about 3.5 Earth radii, the center of the van Allen belt. Apollo astronauts passed through this altitude well below the equatorial plane. Hopefully, astronauts aimed for construction orbits will only pass through twice per extended mission; in construction orbit they will have much more shielding. If the two-time dose is too much, they will need heavy, hydrogen-rich shielding; this extra mass (which could be fuel or plastic cargo) will reduce the number of astronauts that can be launched per vehicle.
Construction orbit
All components will need some initial thrust to raise perigee well above LEO, away from satellites crowded into high inclination orbits near the Earth. At the first apogee, the initial perigee radius of 6378+80 = 6458 km will be raised to 8378 km with a relatively small and inexpensive thrust package, about 114 m/s of ΔV in the prograde direction. It is more important that this initial thrust device is inexpensive, high thrust, reliable and accurate, rather than high IISP.
The exhaust from a rocket at these high altitudes will leave the vehicle faster than orbital velocity, and will end up in solar orbit. In the far future, we do not want to fill cislunar space with a thin cloud of rocket exhaust, when we are launching billions of tonnes into orbit per year. Note that the last dregs of exhaust from solid fuel rockets are sand and clinkers, because the stoichiometry of combustion becomes very unbalanced and stops before the remaining propellant is consumed; I hope we can avoid solid rockets in the future.
- Note that returning crews from the transfer orbit requires a retrograde -114 m/s of ΔV, which drops perigee back down into the atmosphere 12 hours later. A few more meters per second will drop perigee into thicker atmosphere for a more rapid descent. A similar 12 hour descent will be required in an emergency, and it may take as long as 26 hours (worst case) to return a wounded astronaut to the ground. A higher construction orbit requires a little less ΔV to enter, but the extended return time and slower supply cadence makes higher orbits less valuable. With a launch loop providing ultracheap launch ΔV, reducing production time is more important than reducing propellant use.
- For fast emergency return, an "ambulance" may have vastly more propellant and ΔV, and interrupt the orbit for a fast descent and high speed reentry from any part of the orbit. It might be better to invest the effort in a capable orbiting emergency hospital in every construction; with launch loop we can afford the mass budget. Such mini-hospitals (with a world of medical professionals available using predictive adaptive telepresence) should be an early goal for construction orbit station design, and will contribute to interplanetary mission design.
The construction orbit will have a 86164.0989 second period, one stellar day, with perigee at 8 degrees south latitude. The launch loop (also at 8 degrees south latitude) will rotate underneath perigee once per day, to add another string of 5 tonne components to the assembly.
The first component launched will be a thrust "tractor", with enough precision ΔV capability to rendezvous with subsequent vehicles and rendezvous with the accumulating construction station. Subsequent vehicles should arrive ready for collection by orbital tugs stationed beforehand in construction orbit, which will perform the low ΔV capture, maneuvering and final rendezvous with the construction station.
Tanks of fuel will be delivered next; these will double as radiation shielding for construction workers and radiation sensitive components as the construction orbit passes through the radiation belts, once per day.
The high eccentricity construction orbit moves at high velocity near the earth, low velocity far from it, less than 6 hours per day below geostationary altitude. While the total radiation dose will be higher than an alternative circular construction orbit at GEO altitude, the dose for 18 hours a day will be much lower. Astronauts aboard the construction station will sleep in tubes between the fuel and water tanks for the 6 hours of high radiation dose, and will receive much less total radiation dose than they would in the circular orbit.
Although I have not done the calculation, if there are hundreds of thousands of tonnes of low-Z atoms orbiting daily through the center of the radiation belts, that will absorb or scatter most of the low and medium energy protons. This could rapidly attenuate the total trapped ion population in the radiation belts. In time, this could make space travel much safer.
Eliminating most of the belt also greatly reduces the equatorial ring current, which is the mechanism that couples coronal mass ejections from the Sun to "Carrington Event" magnetic field changes on the Earth. If this works as expected, this will protect the terrestrial power grid from the large ground loop voltages that can damage it during solar storms.
Construction orbits will be used to assemble high altitude mega-structures, such as space solar power satellites and space colonies. They will also be the source and the return destination for reusable interplanetary vehicles, such as Aldrin Mars Cyclers.
What does a construction orbit look like?
Here is a plot of the (stellar) daily position of construction stations as viewed from the fixed stars:
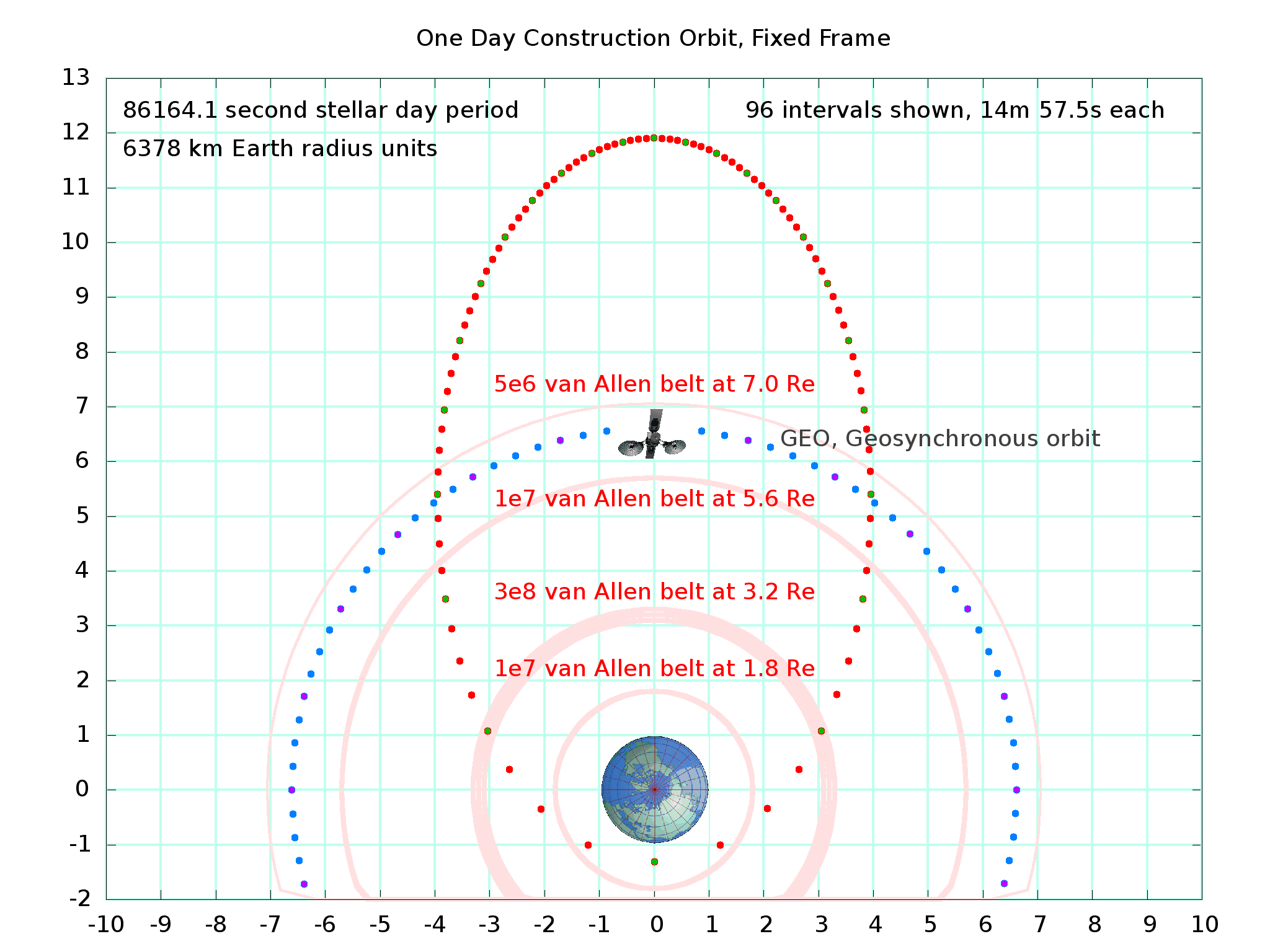
The grid is in "Earth equatorial radii", 6378 kilometers per grid cell. 96 dots per 86184 stellar day period, a bit less than 15 clock minutes between dots, with every 4th dot accented to represent a "stellar hour". A comsat in geostationary orbit is shown; comsats will be needed to relay communications to Earth stations below during part of the orbit. Note that a construction station spends less than 6 hours below GEO. Construction workers will sleep in shielded areas during this portion of the orbit.
Here is a plot of the same orbit viewed relative to the rotating Earth:
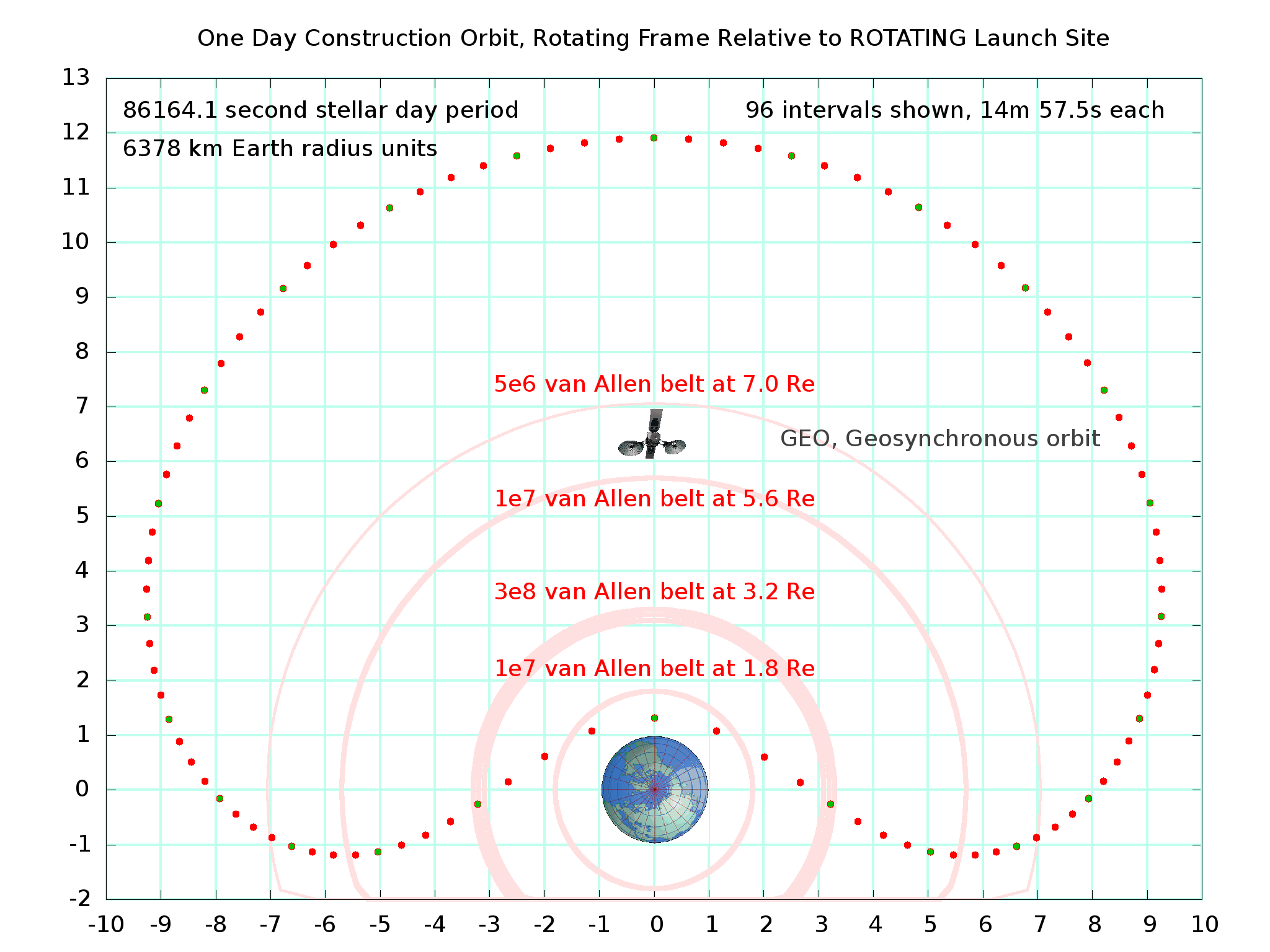 ]]
]]
The actual orbit is not kidney bean shaped, of course; this is merely how it appears from our rotating vantage point. The construction orbit perigee (and apogee 12 stellar hours later) are both at the same latitude as the launch loop, shown here at 120 degrees west longitude, due south of the west coast of the United States. However, the station is only visible for about 10 minutes before and after perigee, dropping below the horizon for 5 hours before and after. For about 12 hours of every orbit, communications to the launch loop area itself must be relayed through communication satellites in geosynchronous orbit, or via other stations in construction orbit. Note also that due to the inclination of the construction orbit, apogee will be 8 degrees north of the equator.
This constellation of orbits (each of the points represents a large, permanent construction station) will be the hub of activity associated with a launch loop. Additional launch loops will be built to the east closer to the South American coast, and west towards French Polynesia; so there will be many non-intersecting constellations. Traffic management for these orbits will require global coordination, and will require continual tweaking to correct for tidal perturbations from the Moon, Sun, and Jupiter, but we will eventually orbit billions of tonnes of construction stations as waypoints to the rest of the solar system.
Think BIG.
Here is the C program that computed the numbers, and the gnuplot control file that produced the pretty pictures. I would like to change how the van Allen belts are depicted, as a sheaf of thin gray lines representing the density of the belt, but I have more important tasks to complete first.
But how do we get from an inclined construction orbit to a circular equatorial GEO orbit? One way is with another small ΔV thrust at apogee to raise perigee, then make a second larger ΔV thrust as this orbit crosses the equatorial plane at GEO radius to circularize the orbit.
My hunch is that we should leave the inclination, and some of the eccentricity, so that the target orbit follows a Lissajous pattern in the sky - for space solar power, the idea is to concentrate availability during the peak load period between 5 to 10 pm on the Earth below. If the SSPS appears at a higher latitude in the sky, this reduces interference with communication satellites to the south, and reduces the slant angle at which the beam arrives, reducing the size of both the power satellite transmitter and the rectenna farms below. Such complexities may bother those who like simple pictures, but they are how global economies comprising billions of contributors actually work. Oversimplification is for children and dictators, not profit-maximizing entrepreneurs and the clever engineers they hire.
All that said, less clever engineers prefer circular equatorial orbits, so that's what the following maneuver will deliver. Just be aware that more clever engineers will be more efficient, and out-compete (and out-maneuver) the less clever.
Transfer orbit 1
The orbits will look approximately like so (in relation to the fixed stars), inclination is not shown:
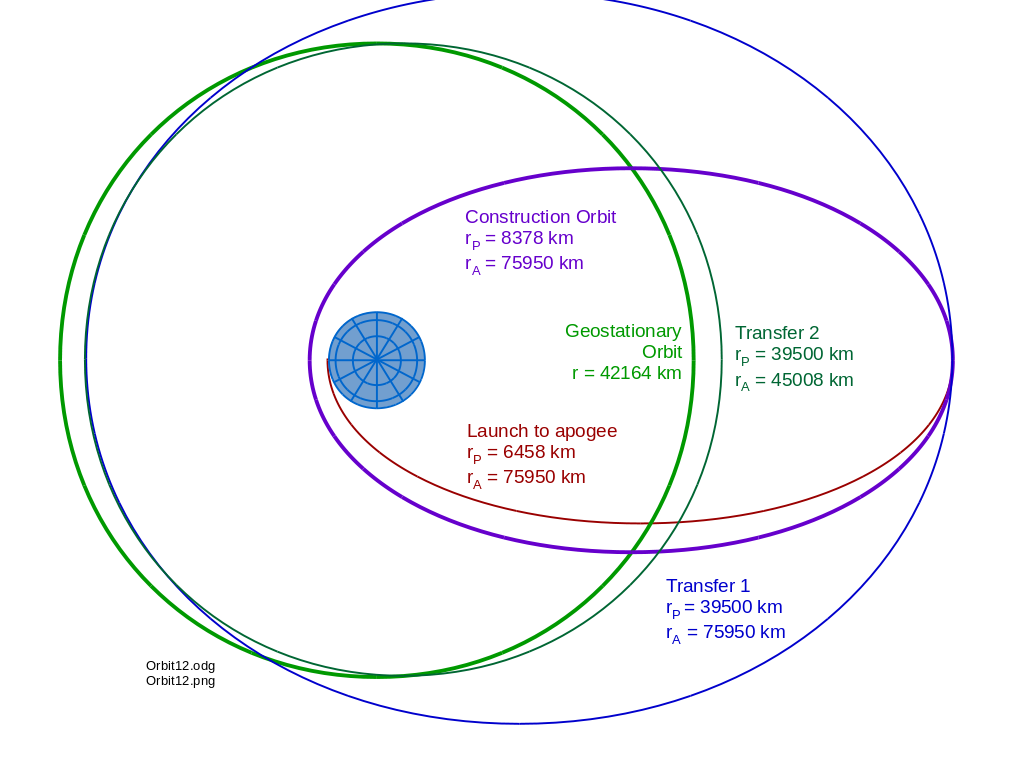
After construction, the first maneuver raises perigee with an 873 m/s prograde ΔV at apogee. Typically, the transfer vehicle will only remain in this orbit for half an orbit. However, if a high ISP electric rocket is used, this maneuver may conserve fuel but take weeks. This might be the case if the transfer vehicle is a completed space solar power satellite; lots of power, small electric rocket - which will also be used for subsequent manuevers, as well as stationkeeping in the destination orbit.
Note: in the abstract, we could also make the transition to transfer orbit 2 by lowering apogee first. However, high is slow, and maneuvering from a lower orbit uses more propellant than maneuvering from a higher one.
Transfer orbit 2
Transfer orbit 2 is an 8 degree inclined and slightly elliptical orbit that crosses geosynchronous orbit with a radius of 42164 km = a ( 1 - e^2 ) = 2 ( r_p r_a ) / ( r_p + r_a ) . A 366 m/s retrograde thrust at 39500 kilometer perigee drops apogee down to 45213 kilometers. A vehicle with a high ISP rocket typically spends a bit more than six hours making one quarter of an orbit from perigee to the final thrust. As before, if a high ISP electric rocket is used, this may take many orbits.
Circular GEO
The last thrust is complicated, a combined three axis 906 m/s thrust that circularizes, decellerates, and planarizes the orbit simultaneously (the vector sum of three vectors is smaller than each component separately). Most of this large thrust is not necessary if the SSPS is allowed to operate in an inclined and slightly elliptical orbit.
Construction Orbits for Interplanetary and Lunar Missions
Some say "orbit is halfway to anywhere", but geosynchronous orbits are actually about the farthest "anywhere" that a launch loop will usually aim at. To go further out, we start at with a construction orbit, but add velocity at perigee; 392 m/s at perigee puts the vehicle in a lunar transfer orbit, a few kilometers per second will put it into a slow (or fast) interplanetary orbit to Mars or Venus. An interplanetary orbit with another large thrust close to Venus is the cheapest way to get to the outer solar system; however, opportunities are so rare that it is better to use big chemical engines with A LOT of ΔV at perigee to do this.
My own preference for near-term "interplanetary" missions is a myriad of small near Earth asteroids, staging bases for long period cyclers to more distant destinations. It's a huge solar system, and distant missions will take years; accept it. The solar system is 4.6 billion years old, and we will fill it with life in a tiny fraction of that time. Extend life and take it easy; if you are in a hurry, digitize yourself and travel at the speed of light, which will be perceptually instantaneous to any destination in the galaxy.
