|
Size: 2535
Comment:
|
Size: 4139
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 30: | Line 30: |
| || H kg || 240000 || 32000 || 4700 || 2600 || 1900 || 1700* || 1000 || 2300 || 1300 || 1300* || 1200 || | || H kg || 240000 || 32000 || 4700 || 2600 || 1900 || 1700* || 1000 || 1500 || 1300 || 1300* || 1200 || |
| Line 53: | Line 53: |
----- === 24 hour "Construction" Orbit === '''Note:''' 75950 km radius is the apogee of a "24 hour" geosynchronous (but NOT geostationary) orbit with a 8378 km radius (2000 km equatorial altitude) perigee. The same 42164 km semimajor axis as a circular geostationary orbit. This is a High Eccentricity Earth Orbit (HEEO), suggested by space scientist John Lewis at the University of Arizona. Given the high perigee velocity of a launch loop, this orbit is easier to achieve with much less apogee insertion ΔV than a GEO orbit. The perigee velocity of this HEEO orbit is high, and that is an excellent place for a high ΔV thrust into an interplanetary trajectory. '''Subnote 1:''' due to the J₂ nonlinearity of the Earth's gravity field, this orbit will precess, so an exact synchronous orbit will have a slightly smaller semimajor axis. '''Subnote 2:''' launchloop launches slows portions of the rotor; restoring rotor position and velocity requires enormous power. Larger vehicles would slow the rotor more, requiring more peak electrical power generation capacity. It is cheaper to assemble large interplanetary vehicles at a permanent orbiting construction station from dozens, perhaps hundreds of daily launches, then launch the propellant to fuel them after they are assembled. Since a launch to an interplanetary Hohmann must occur at a specific time of day for a particular mission, the perigee of the construction orbit must occur at that specific time. This is an annoying constraint for infrequent Mars missions, but less so for missions to many different asteroids. |
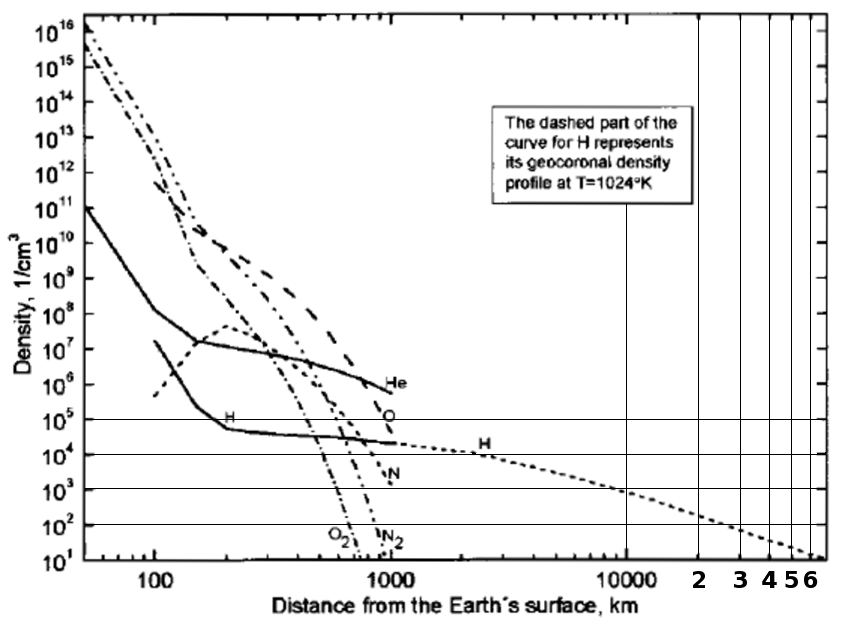
Propellant Plume Gas Scattering
H density versus altitude
|
alt km |
radius km |
#/m3 |
1000 |
7378 |
21000e6 |
|
2000 |
8378 |
12000e6 |
Constr. perigee |
5000 |
11378 |
3100e6 |
|
10000 |
16378 |
820e6 |
|
20000 |
26378 |
180e6 |
|
30000 |
36378 |
67e6 |
|
35786 |
42164 |
45e6 |
GEO circular |
40000 |
46378 |
35e6 |
|
50000 |
56378 |
22e6 |
|
60000 |
66378 |
14e6 |
|
69572 |
75950 |
11e6 |
Constr. apogee |
70000 |
76378 |
10e6 |
|
. https://www.sciencedirect.com/science/article/pii/0022407372900052
Estimated hydrogen mass per 1000 km height, 1.67e-27kg/H |
|||||||||||
Altitude km |
1000 |
2000 |
10000 |
20000 |
30000 |
35786* |
40000 |
50000 |
60000 |
69572* |
70000 |
Radius km |
7378 |
11378 |
16378 |
26378 |
36378 |
42164* |
46378 |
56378 |
66378 |
75950* |
76378 |
Volume km³ |
6.8e11 |
1.6e12 |
3.4e12 |
8.7e12 |
1.7e13 |
2.2e13 |
2.7e13 |
4.0e13 |
5.5e13 |
7.2e13 |
7.3e13 |
#H / m³ |
2.1e10 |
1.2e10 |
8.2e8 |
1.8e8 |
6.7e7 |
4.5e7 |
3.5e7 |
2.2e7 |
1.4e7 |
1.1e7 |
1.0e7 |
H kg |
240000 |
32000 |
4700 |
2600 |
1900 |
1700* |
1000 |
1500 |
1300 |
1300* |
1200 |
Less than 20 tonnes of hydrogen (and almost nothing else) above GEO, out to the bow shock.
Collision cross section table
Gas |
(nm)² |
(nm)² with H₂ |
H₂ |
0.27 |
1.02 |
He |
0.21 |
0.99 |
Ar |
0.36 |
1.06 |
O₂ |
0.40 |
1.07 |
N₂ |
0.43 |
1.08 |
CH₄ |
0.46 |
1.09 |
CO₂ |
0.52 |
1.11 |
Cl₂ |
0.93 |
1.22 |
The second column is the combined collision cross section with an H₂ molecule ... the square of the sum of the square roots.
from libretexts
http://hitran.org . . . . . . . . . k*l at k*l dot com on kao3
24 hour "Construction" Orbit
Note: 75950 km radius is the apogee of a "24 hour" geosynchronous (but NOT geostationary) orbit with a 8378 km radius (2000 km equatorial altitude) perigee. The same 42164 km semimajor axis as a circular geostationary orbit. This is a High Eccentricity Earth Orbit (HEEO), suggested by space scientist John Lewis at the University of Arizona. Given the high perigee velocity of a launch loop, this orbit is easier to achieve with much less apogee insertion ΔV than a GEO orbit. The perigee velocity of this HEEO orbit is high, and that is an excellent place for a high ΔV thrust into an interplanetary trajectory.
Subnote 1: due to the J₂ nonlinearity of the Earth's gravity field, this orbit will precess, so an exact synchronous orbit will have a slightly smaller semimajor axis.
Subnote 2: launchloop launches slows portions of the rotor; restoring rotor position and velocity requires enormous power. Larger vehicles would slow the rotor more, requiring more peak electrical power generation capacity. It is cheaper to assemble large interplanetary vehicles at a permanent orbiting construction station from dozens, perhaps hundreds of daily launches, then launch the propellant to fuel them after they are assembled. Since a launch to an interplanetary Hohmann must occur at a specific time of day for a particular mission, the perigee of the construction orbit must occur at that specific time. This is an annoying constraint for infrequent Mars missions, but less so for missions to many different asteroids.