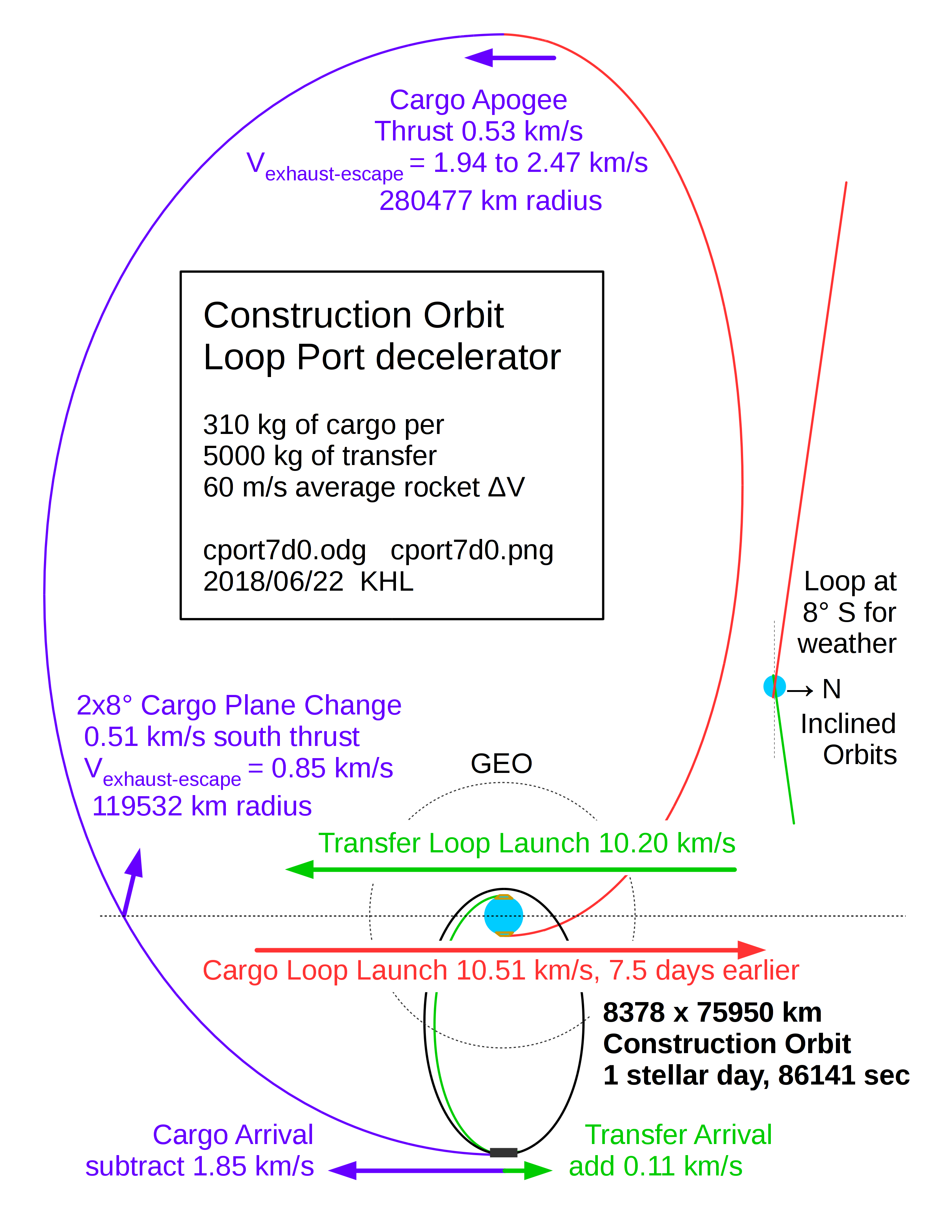
Construction Port
An Arnold-Kingsbury Space Port in a construction orbit, fed by a launch loop. Two streams of vehicles meet at the construction port at the 75950 km (radius) apogee of the geosynchronous (but not circular and geostationary!) 86164 second (one stellar day, which is a solar day minus 3 minutes and 56 seconds) construction orbit.
|
Direct transfer vehicles launch from the loop at 10,200 m/s (surface relative) to an apogee of 75950 km. However, they start with a perigee of 6458 km, not 8378 km like the construction orbit, so they arrive with a velocity deficit of 114 m/s. They are accelerated to construction port velocity in a "short" (1000 meter) Arnold-Kingsbury spaceport at 0.7 gees. |
Slow cargo vehicles launch from the loop at 10,520 m/s to an apogee of 294730 km, approximately 7.5 stellar days before the launch of direct transfer vehicles. At apogee, an additional thrust of 503 m/s increases orbit velocity and raises perigee. |
|
Both vehicles should be timed to arrive nearly simultaneously. This will minimize torque and displacement on the loop-port. Both vehicles will have "mousefart" thrusters for precision (millimeters!) alignment with the loop-port capture rails. |
|
Libreoffice drawing source file |
The two cargo orbit thrusts at a 90° angle from each other may provide enough degrees of freedom to correct large tidal perturbations from the Moon and the Sun (and small perturbations from Jupiter and Saturn). The high apogee of the cargo orbit will amplify the effect of these forces, which will vary over the month and the year.
As an alternative to thrusters, rubber panels on the side of the vehicles may be laser-ablated to produce thrust. This will require a constellation of cooperative lasers.
Vehicle position and orientation can be laser-measured to micrometer accuracy. This surprising capability is used to measure the positions of the LAGEOS Laser Geodynamics Satellites, from the ground, through a turbulent atmosphere, with such high precision that the continental drift under the ground observatories can be measured. In vacuum, without seismic disturbances, accuracies can be fantastically high. LIGO measures differential distances to 23 decimal places, so 11 decimal place interferometric position measurement for sub-millimeter-precision orbit estimation may be possible. We may need even better precision for adjusting the phasing of space solar power satellites to minimize sidelobe communication interference.
The numbers above were calculated in the Libreoffice spreadsheet, the second tab labelled ConPort7d. Feel free to download and tinker with the spreadsheet. Page 2 of the pdf has the hard copy numbers.
Why not launch direct, into the same plane?
To deliver the cargo vehicles with the maximum velocity and angular momentum to the loop port apogee (at 75950 km radius), the apogee of the cargo orbit must be much higher, and on the opposite side of the Earth, where the launch loop was when it rotated through the plane. Remember, the loop launches at a fixed azimuth (along a latitude line) and elevation (close to local horizontal). The direct apogee for that launch, in that plane, is in the exact opposite of the sky. Shifting that apogee requires a huge amount of thrust at perigee. Bad idea.
Pages 5 and 6 of the spreadsheet, ConPortSamePlane, analyzes this possibility. Since the delivery orbit to the loop port must have a very high apogee on the opposite side of the sky (where the launch loop was at the original launch time), we must create that new high apogee by adding velocity at the old high apogee for the cargo vehicle. This is a relatively expensive maneuver, but it is cheaper if we do it at very high altitudes. I chose 439699 km radius for the initial apogee, and also for the new "apogee", making a circular orbit beyond the radius of the Moon. Let's be optimistic and assume the Moon is on vacation, because the numbers are worse with a lower orbit. The ΔV for circularization is 790 m/s.
Half an orbit later (close to a month!) we arrive at the new apogee point, on the opposite side of the sky from the loop port apogee. Now we will subtract 435 m/s of orbital velocity, to drop perigee to meet the loop port apogee. No plane change needed, but at an immense cost in in-plane maneuvering. The relative velocity scaling is a wee bit better; the cargo vehicle arrives at 1971 m/s, and decelerates at 200 gees in the 1000 meter long loop port. However, we expended much more delta V to get there; system average ΔV rises from 58 m/s to 75 m/s, while cargo transit time increases to 30+ days.
ConPort30d, page 4 of the pdf spreadsheet, shows a better use of a superhigh apogee and a 30 day cargo transit, resulting in a mere 35.5 m/s system average ΔV.
However, the Moon is not likely to take a vacation, so neither of these orbits is practical.
I have not analyzed orbits in other than the "0" and "180" degree planes; a "90" degree plane 6 solar hours away from the construction orbit plane may work better. Feel free to do the more complicated geometry and math and inform me of the numerical results. I am not interested in qualitative guesses.
Propellant Velocities
I am still doing journal research to learn about the quantitative behavior of rocket exhaust plumes. These are not clean streams of same-velocity gas, but are scattered by angle and velocity. Some papers report ice crystals emitted from the Apollo / Saturn V third stage liquid hydrogen engines, suggesting just how complex and thermally varying the exhaust plume can be.
My concern is a gigatonne-in-orbit future, where some fraction of the exhaust plume remains in Earth orbit. Other papers report serious contamination issues; propellant plumes have degraded space probe optics and sensors. The worst case for cislunar space is an abundance of propellant plume material clearing out slowly, and an abundance of valuable surfaces that it can run into; mirrors, photovoltaics, windows, and so forth. Damage increases the Strehl scattering of an optical surface, turning it cloudy and white. A piece of flat white paper is a mirror with maximum Strehl scattering.
So, we want to put those gigatonnes in orbit with as little propellant expenditure as possible, and make sure most of the exhaust plume either drops into the atmosphere, or is ejected into interplanetary space, well beyond the orbit of the Moon. The Moon itself is a deep enough gravity well that it will (eventually) collide with and capture much of the gas and particulates whose orbits it intersects with.
The last page of the spreadsheet, PropellantVelocities, is the beginning of some estimates of where the exhaust plumes from cargo vehicle passages end up. My guess is that most (but not all!) of the plumes will escape into interplanetary space, or collide with the Moon, but I cannot quantify that guess, so please be very skeptical. I hope someone reading this page is knowledgeable enough to make an informed and defensible calculation, perhaps suggest changes to the cargo vehicle thrust stages that will shape their plumes to reliably leave cislunar space.
There may be a plume problem in translunar space someday, but the dimensions of the solar system "donut" where the plume ends up is more than 100 million times larger. My apologies to intelligences millions of years from now for my casual disregard of this far future problem. Perhaps not even far future; 10,000 times the plume mass multiplied by 10,000 times as many targets will generate an equivalent total event rate "out there". Bummer, if you are that rare event.