|
Size: 24471
Comment:
|
← Revision 66 as of 2021-06-20 03:27:51 ⇥
Size: 38559
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| ## page was renamed from GEOrail | |
| Line 2: | Line 3: |
| = GEO Rail = == "Landing" Launch Loop payloads in a destination without rockets == Imagine a long and heavy orbiting tether, running vertically from 29900 km radius, through GEO (42164 km), to a counterweight above. The tether has a thin, passive conductive rail around it. It will be used to magnetically capture vehicles and move them to GEO, using the sliding rail to push payloads transversely while they magnetically slide upwards. This is not the normal apogee capture system, where we launch into an orbit whose perigee transverse velocity matches a hanging tether at the right altitude. Instead, we launch the vehicle a little faster and a little later. That puts the vehicle in an orbit with an apogee trailing the tether. The vehicle will never get to that apogee, because we will slide in front of the tether below apogee, where we still have a high (1800 m/s) radial velocity. We will still match the tether's transverse velocity and altitude, though. In the rotating tether frame of reference, the vehicle will approach from below at high speed, from the rear, and decelerate in the traverse ("horizontal") direction as it approaches the tether. The vehicle is rising radially, conserving angular momentum, and losing angular velocity as the radius increases. In the tether's rotating frame, this looks like Coriolis acceleration, equal to twice the velocity times the tether's angular velocity. The angular orbital velocity for a GEO tether is 7.2921E-5 radians per second, and the radial ("vertical") velocity will be around 1800 meters per second, so the Coriolis acceleration is 0.26 m/s^2^. If the vehicle misses the tether rendezvous, it will continue to accelerate retrograde in the rotating frame, with the backwards velocity turning into downwards Coriolis acceleration in the rotating frame, reaching apogee above the intended attach point but well below GEO. |
= Capture Rail = === "Landing" Launch Loop payloads on tethers in circular orbit, without apogee kick motors === . ''More rockets bite the dust ...'' The launch loop provides low cost delta-V from the earth's surface, injecting vehicles into highly elliptical transfer orbits, or earth-escape orbits. What a launch loop cannot do directly is put a payload into a circular orbit. The perigee of a launch-loop launch will always be at the launch track height, even if the apogee reaches the moon. To put a vehicle into a higher circular orbit requires additional angular momentum, usually supplied by a rocket. Tethers provide an alternative. A zero-velocity capture on a vertical tether means that the launch loop launches payloads with an angular velocity matching that of the tether, at a lower altitude ( or radius ) than the center of the tether's orbit. == Classic Tether Capture == '''Yellow is a vehicle in a transfer orbit from launch. Green is a capture, red is a missed capture.''' {{ attachment:cap12.png | | width=960, height=320 }} [[ attachment:cap12.c | Here is the source ]] , and you will need [[ http://www.libgd.org/ | libGD ]] and [[ http://apngasm.sourceforge.net/apngasm | apngasm ]]. Capturing on a tether is not a new idea. The transfer orbit is chosen such that the vehicle arrives at the tether with zero velocity, and clamps on. It will have a small relative acceleration downwards, perhaps 2.5% of one gee, a fairly light load, assuming the tether is much more massive than the vehicle. There are problems with classic tether capture. For a tether in geostationary orbit, capturing a vehicle in a transfer orbit with a perigee of 80km, the capture radius (the apogee of the transfer orbit) is at 29870 km, 12294 km below the geostationary altitude of 42164 km. Somehow, the vehicle must climb up the tether for more than 12000 kilometers. With the very small gee loading, this is not nearly as difficult as climbing up a space elevator from the Earth's surface, and a tractor vehicle can be waiting on the tether to pull up the launch vehicle. However, with limited power and wheel velocity, this will still take a while. At 200 kilometers per hour, the climb will take 61 hours. The climb will probably be slower on the higher gee lower section. We will be stealing angular momentum from the tether, so we will need something like a VASIMR electric rocket to add the momentum again. Worse still, what if we miss the capture? The period of the circular transfer orbit is 6.768 hours; the next time the vehicle reaches apogee, the tether will be a long way away, and we may need many days and hundreds of meters per second of delta V to catch it again. == Climbing Tether Capture == {{ attachment:cap11.png | | width=960, height=320 }} [[ attachment:cap11.c | Here is the source]], and you will need [[ http://www.libgd.org/ | libGD ]] and [[ http://apngasm.sourceforge.net/apngasm | apngasm ]]. But who says the vehicle is constrained to zero vertical/radial velocity? Vehicles leave the launch loop with a magnetic rail attached to the bottom, which magnetically drags on the rotor and propels them to orbital speeds. The magnetic rail is passive - it can only produce drag - but it can drag on anything conductive, such as a very thin metal tube around a tether. If we arrive at the tether with zero transverse/horizontal velocity, and a high radial/vertical velocity, we can ride the magnetic rail, just like the launch loop track that we left a few hours before. As we ride up the rail, we slow down against it. In a matter of minutes, we brake to a stop at geostationary radius. This requires a few percent more deltaV at launch, but launch velocity is cheap with a launch loop. Transit time from start of launch to arrival at GEO will be less than 4 hours. The transit time will be slightly faster than a classic Hohmann transfer orbit with an apogee kick motor. Other benefits include a somewhat shorter hanging tether, which also reduces the amount of angular momentum the vehicle removes from the tether. For a geostationary target orbit, we can choose a transfer orbit with a 12 hour period and a semimajor axis of 26562 km (0.62996 smaller semimajor axis than the 42164 km GEO orbit). If apogee remains at launch loop exit altitude (6458 km), then drag can help the vehicle reenter 12 hours later, on the other side of the earth from the launch loop. It we instead choose to make another try, we can add 10m/s deltaV at apogee, and raise perigee by 45 km, a 200x reduction in drag. That will give us one or two more passes at capture, 24 and 48 hours later. The unmodified orbit is the "12 hour low" orbit, while the boosted perigee orbit is the "12 hour high" orbit. Actually, we must also perform a second burn at perigee, to lower apogee, if we wish to maintain the same semimajor axis and the same 12 hour orbit period. We can also choose a transfer orbit with a 24 hour complete period, and perform the same perigee-raising maneuver if we wish to reduce drag and make a second pass. That higher orbit will have higher angular momentum, and draw less angular momentum from the tether. || Transfer Orbit ||Perigee|| Apogee||V,,P,,||V,,A,,|| AngM ||R,,capture,,|| || || km || km || m/s || m/s || m^2^/s|| km || || 12 hour low || 6458 || 46665 || || || || || || 12 hour high || 6503 || 46620 || || 24 hour low || 6458 || 77870 || || 24 hour high || 6503 || 77825 || A 24 hour orbit, geostationary capture tether, fed from a fixed point on earth, is perhaps the easiest capture tether to imagine. However, a non-synchronous capture tether offers more flexibility, as we will see below. ---- THE REST OF THIS PAGE WILL BE REWORKED ---- Imagine a long and heavy orbiting tether, running vertically from 29000 km radius, through GEO (42164 km), to a counterweight above. The tether has a thin, passive conductive rail around it. It will be used to magnetically capture vehicles and move them to GEO, using the sliding rail to push payloads transversely while they magnetically slide upwards. This is not the normal apogee capture system, where we launch into an orbit whose perigee transverse velocity matches a hanging tether at the right altitude. Instead, we launch the vehicle a little faster and a little later. That puts the vehicle in an orbit with an apogee trailing the tether. The vehicle will never get to that apogee, because we will slide in front of the tether below apogee, where we still have a high (2700 m/s) radial velocity. We will still match the tether's transverse velocity and altitude, though. In the rotating tether frame of reference, the vehicle will approach from below at high speed, from the rear, and decelerate in the traverse ("horizontal") direction as it approaches the tether. The vehicle is rising radially, conserving angular momentum, and losing angular velocity as the radius increases. In the tether's rotating frame, this looks like Coriolis acceleration, equal to twice the velocity times the tether's angular velocity. The angular orbital velocity for a GEO tether is 7.2921E-5 radians per second, and the radial ("vertical") velocity will be around 2700 meters per second, so the Coriolis acceleration is 0.27 m/s^2^. If the vehicle misses the tether rendezvous, it will continue to accelerate retrograde in the rotating frame, with the backwards velocity turning into downwards Coriolis acceleration in the rotating frame, reaching apogee above the intended attach point but well below GEO. |
| Line 13: | Line 70: |
| We launch a vehicle off the launch loop at 10148.7 m/s, and with very good radar and some trim thrusters, we "land" on the bottom of the rail at 29979.7 km altitude. At that point, we have the same angular frequency and circular orbital velocity, and a large vertical velocity component, 1746.8 m/s . As the vehicle slides up the tether, the weak gravity slows it down radially, as it accelerates forwards in orbit to remain on the "faster at higher altitude" tether. As the vehicle slides upwards, it magnetically levitates/pushes against the east side of the rail with Coriolis acceleration. That is 26 centimeters per second squared at 1800 m/s vertically, and 7 centimeters per second squared at 400 m/s, our speed as we approach GEO altitude. The Coriolis acceleration and the eddy currents both reduce with relative velocity - most convenient! The vertical deceleration (gravity minus rotational centrifugal acceleration) decreases to zero as we approach GEO, still with significant velocity, though with less than the velocity of a frictionless ballistic because of the eddy currents. As the vehicle approaches GEO, it is still moving fast, which is good, because it has 12000 kilometers to travel. The trip will take about 4 hours. About 10000 meters below GEO station, the rail surface changes to increase eddy current drag, slowing down the vehicle. The vehicle reaches the drag section at 400 meters per second, and deceleration increases from a few millimeters per second to 10 m/s^2^, a bit more than 1 gee (with passengers facing backwards, backs into chairs). The vehicle slows to 25 meters per second about 40 meters below the station, and with the aid of some linear motors, reduces deceleration and velocity to zero over the next 5 seconds. The payload or passenger compartment is plucked off the magnet-rail and wing, and pushed into the station through an airlock. Since the tether rail is not magnetic or active (that would be far too heavy for a 12000 kilometer gossamer structure) the vehicle magnet-rail will need to wrap partly around it in some way. 26 cm/s^2^ Coriolis acceleration is far too weak to hold the vehicle against a rippling tether at high speed. For example, a ripple with a 20 kilometer wavelength and a 20 meter peak-to-peak amplitude will shake the vehicle back and forth at 0.3 gees ( 12x Coriolis ) and a period of 11 seconds - a mild roller coaster. Such a transverse ripple will not be a standing wave, but traveling up or down the tether at around 1 km per second. It will be a challenge to remove it, perhaps by periodic transverse shaking at GEO by the large momentum mass. It would be more difficult to remove by shaking the bottom counterweight vertically, inducing Coriolis accelerations, because a lot of power is required. |
We launch a vehicle off the launch loop at 10463 m/s, and with very good radar and some trim thrusters, we "land" on the bottom of the rail at 30440 km altitude. At that point, we have the same angular frequency and circular orbital velocity, and a large vertical velocity component, 2700 m/s . As the vehicle slides up the tether, the weak gravity and eddy current drag slows it down radially, as it accelerates transversely (forwards) in orbit to remain on the "faster at higher altitude" tether. As the vehicle slides upwards, it magnetically levitates/pushes against the east side of the rail with Coriolis acceleration. That is 39 centimeters per second squared at 2700 m/s vertically, and 19 centimeters per second squared at 1334 m/s, our speed as we approach GEO altitude. The Coriolis acceleration and the eddy currents both reduce with relative velocity - most convenient! The vertical deceleration (gravity minus rotational centrifugal acceleration) decreases to zero as we approach GEO, still with significant velocity, though with less than the velocity of a frictionless ballistic because of the eddy currents. As the vehicle approaches GEO, it is still moving fast, which is good, because it has 12000 kilometers to travel. The trip will take about 5 hours from earth, and 2 hours riding up the tether. It will be slower than a Hohmann with an apogee kick motor, but much cheaper and less polluting. At "slowdown height", about 180 kilometers below GEO station, the rail surface changes to increase eddy current drag, slowing down the vehicle. The vehicle reaches the drag section at 1334 meters per second, and deceleration increases from a few millimeters per second to 5 m/s^2^, a bit more than half a gee (with passengers facing backwards, backs into chairs). The vehicle slows to 25 meters per second about 40 meters below the station, and with active track control, reduces deceleration and velocity to zero over the next 5 seconds. The payload or passenger compartment is plucked off the magnet-rail and wing, and pushed into the station through an airlock. Since the tether rail is not magnetic or active (that would be far too heavy for a 12000 kilometer gossamer structure) the vehicle magnet-rail will need to wrap partly around it in some way. 39 cm/s^2^ Coriolis acceleration is far too weak to hold the vehicle against a rippling tether at high speed. For example, a ripple with a 20 kilometer wavelength and a 20 meter peak-to-peak amplitude will shake the vehicle back and forth at 0.8 gees ( 12x Coriolis ) and a period of 7 seconds - a frisky roller coaster. Such a transverse ripple will not be a standing wave, but traveling up or down the tether at around 1 km per second. It will be a challenge to remove it, perhaps by periodic transverse shaking at GEO by the large momentum mass. It would be more difficult to remove by shaking the bottom counterweight vertically, inducing Coriolis accelerations, because a lot of power is required. |
| Line 27: | Line 84: |
| More rockets bite the dust ... |
|
| Line 35: | Line 90: |
| === VASIMR and "Zero Orbiting Exhaust" momentum restoration === |
|
| Line 39: | Line 96: |
| A [[ http://en.wikipedia.org/wiki/VASIMR | Variable Specific Impulse Magnetoplasma Rocket ]] (VASIMR) engine operates optimally at 50 km/sec, so operation at 80 km/sec is close to optimum. The reaction mass is argon, which can be frozen at -200C with a density of 1600 kg/m3 and a vapor pressure of 0.1 atmosphere for transit from earth. We will need about 1 kg of argon reaction mass shipped up for every 50 kg of uncompensated mass shipped up from Earth. Argon is 0.93% of the atmosphere, and costs about $1/kg (liquid) in high quantities. It is a byproduct of the production of liquid oxygen. We will expend about 40 kilowatt hours per "uncompensated vehicle kilogram" operating the plasma rockets, including coolers and radiator operation. Typical solar cell weights for existing satellites are 65 kg/kilowatt, so 1 kilogram of solar cells provides enough energy in a year to bring aboard 3.5 kilograms of mass - a power doubling time of 5 months. However, if we can use "server sky" style ultra-thin InP cells, closer to 1000 kg/kW, we can approach 50 kilograms of mass per kilogram of solar cell. In the very long term, solar cells made from lunar materials will bring both momentum and cheaper launch to the GEO rail, but solar cells are a high-tech undertaking, and it will be a long time before that level of manufacturing technology can operate practically in space. In the shorter term, we may be forced to get by with lower ISP engines than 80 km/sec VASIMR, perhaps operating only around noon with an exhaust velocity of 20km/sec. That increases our argon needs 4X, but reduces our power needs 16X. We will only be operating our engines with about a 30 percent duty cycle, so our solar panel needs only drop 5.3X. Still, our power doubling time drops to a month or so. Probably worth it during the building phase. We may even be rascals, and run the VASIMR engines 24 hours for a while, dumping a few tons of midnight argon into orbits in the inner solar system. == Operation of an M288 rail base == A similar rail system can supply the M288 [[ http://server-sky.com | server sky orbits ]] MORE LATER == M288 rail bases for orbital debris capture == Server sky thinsats are cheaper to launch if they are lighter, but below a minimum mass-to-area ratio, the orbits are unstable under light pressure. However, we can add mass ballast to a very light satellite, using gram-weight chunks of space debris. The processing is simple, just let the debris shatter as it is collision-captured inside a cornucopia-shaped funnel. Larger chunks can be cut apart at a simple processing plant at the M288 rail base, smaller chunks can be welded together. Capture vehicles can drop below the tether, in intercept orbits where the debris crosses the equatorial plane. Depending on their orbit, they can return to the same rail base, but more likely a different rail base will be more convenient. MORE LATER |
A [[ http://en.wikipedia.org/wiki/VASIMR | Variable Specific Impulse Magnetoplasma Rocket ]] (VASIMR) engine operates optimally at 50 km/sec, so operation at 80 km/sec is close to optimum. The reaction mass is argon, which can be frozen at -200C with a density of 1600 kg/m3 and a vapor pressure of 0.1 atmosphere for transit from earth. We will need about 1 kg of argon reaction mass shipped up for every 50 kg of uncompensated mass shipped up from Earth. Argon is 0.93% of the atmosphere, and costs about $1/kg (liquid) in large quantities. It is a byproduct of liquid oxygen production. With 80km/s exhaust, we will expend about 40 kilowatt hours per "uncompensated vehicle kilogram" operating the plasma rockets, including coolers and radiator operation. Typical solar cell weights for existing satellites are 65 kg/kilowatt, or 16 watts per kilogram, so 1 kilogram of solar cells provides enough energy in a year to bring aboard 3.5 kilograms of mass - a power doubling time of 5 months. However, if we can use "server sky" style ultra-thin InP cells, closer to 1000 kg/kW, we can approach 50 kilograms of mass per kilogram-year of solar cell. In the very long term, solar cells made from lunar materials will bring both momentum and cheaper launch to the GEO rail, but solar cells are a high-tech undertaking, and it will be a long time before that level of manufacturing technology exists in space. In the shorter term, perhaps there is some variant of VASIMR that can operate at lower exhaust velocities, expending more argon but using less energy. If we fire the argon out at 4500 m/s, and don't have too much thermal spread, the argon will be in a ballistic orbit that falls into the atmosphere (returning the argon where we found it). This will require 1 kilogram of argon for every 3 kilograms of payload shipped, which may mean that every other payload is argon during construction. However, at 50% efficiency, and 50% mass fraction we will need only 3.8 kW-hours of energy per kilogram of incoming non-argon mass, resulting in 1 kg per 10 kg-days of solar cell. That will lead to very fast growth rates of the power and engine systems, rapidly evolving towards the high velocity exhaust scenario. The above analysis assumes that the argon plasma neutralizes - if it stays ionized, it will gyrate in the Earth's magnetic field and not go much of anywhere, because the pitch angle will be high. That will be interesting, perhaps the trapped particles will act as shielding mass against higher energy particles trapped on the same field lines, but that analysis must wait for another time. Also - do not assume that we can fire the argon at night at just the right velocity so that the exhaust falls into the sun. The sun is a small target, and distant, so with thermal spread much of the exhaust will end up in highly elliptical orbits that reach earth's orbit. The gas will be dilute, and most of it that returns will collect in the morning sky, but it will add some pollution in the long run. How much argon will we use? The Earth's atmosphere weighs 5E15 tons, and about 1% is argon, so 5E13 tons of argon are available. With 80km/s exhaust resulting in a 50:1 payload-to-argon ratio, we can ship up 2.5E15 tons before we run out of argon. Chances are, we will be shipping down material and momentum from the moon long before we make a dent in the argon supply. == Conductor Track Weight == Assume a 5 ton vehicle moving at 2700m/s with 1.0 m/s^2^ transverse acceleration (lots of vibration!), and 0.3 m/s^2^ radial deceleration from the magnetic field. The total transverse force is 5000N, the deceleration force is 1500N. The deceleration power is 4MW . Assume a 10 meter magnet rail with 0.2T undulating fields and 50% fill, and an average of 4 cm of "track width" on a 6cm diameter aluminum tube (bonded to a Kevlar core tube), so the "bearing surface" is 0.2 m^2^. The field pressure is 5000N/0.2m^2^ or 25000N/m^2^, which is 0.2T times 125,000 amps per meter in the conductor. Assume the current path is effectively 10cm long and 5 meters wide for 625KA total. For a deceleration power of 4MW, the resistance of the current path must be 4MW/(625KA^2^) or 10 micro-ohms. The resistivity per square of the aluminum will be (5.0/0.1) times that, or 500 micro-ohms per square. Aluminum is about 30 nano-ohm-meter, so a thickness of 60 microns will have that resistivity. The cross section is $pi$ * 0.06m * 6E-5m or 1.13E-5 m^2^, for a mass per meter of 30 grams (aluminum density is 2.7). That is 30kg/km, or 360 tons of aluminum for the whole 12000 km track. 4MW/2700m/s, or 1500 Joules per meter of heat energy will be deposited into the 30g/m track. Aluminum heat capacity is 0.9 J/gm-K, so it could heat by about 56K. However, it is bonded to a much larger mass of Kevlar (1.4 J/gm-K), and the thermal diffusion time through 60 microns of aluminum is about 40 microseconds. The 10 meter magnet rail passes by in 3.7 milliseconds, so we can assume that most of the heat has passed into the Kevlar core, and the aluminum heats much less. MORE LATER -------- |
| Line 68: | Line 129: |
| $ a ~ = ~ { \Large { r_p \over { 2 ~ - ~ \LARGE { { r_p {v_p}^2 } \over { \huge \mu } } } } } $ ` ` semi-major axis | $ a ~ = ~ { \Large { 1 \over { \LARGE { 2 \over r_p } ~ - ~ \LARGE { { {v_p}^2 } \over { \huge \mu } } } } } $ ` ` semi-major axis |
| Line 90: | Line 151: |
| ---- |
|
| Line 92: | Line 155: |
| For the classical ( zero vertical velocity ) tether capture, $ v_R $ = 0 and $ \theta $ = $ \pi $ . So: $ {\omega_T} ~ = ~ { \Large { { \mu^2 ( 1 - e )^2 } \over { {r_p}^3 {v_p}^3 } } } $ $ ~ ~ ~ ~ ~ ~ = ~ { \Large { { \mu^2 ( 2 - r_p {v_p}^2 / \mu )^2 } \over { {r_p}^3 {v_p}^3 } } } $ $ ~ ~ ~ ~ ~ ~ = ~ { \Large { { ( 2 \mu - r_p {v_p}^2 )^2 } \over { {r_p}^3 {v_p}^3 } } } $ The perigee velocity $ v_p $ can be computed by iterating on this equation: $ v_p ~ = ~ \sqrt{ 2 \mu / r_p - \sqrt{ \omega_T r_p {v_p}^3 } } $ Given $ v_p $, we can compute the capture radius, which is $ r_a $ as above. But we aren't done! We need to do two more things - climb up the tether, and restore momentum to the tether. Assume the tether is massive compared to a vehicle, so it does not deflect much. The will slow down by a tiny amount, and we must restore the momentum, perhaps with rocket engines. We must also supply energy to lift the vehicle up the tether against the small gravity (minus centrifugal force) at that high altitude. ||<-4:> '''Classical Tether Capture''' || || $ \mu $ || gravitational parameter || 3.986004418e14 || m^3^/s^2^ || || $ \omega_T $ || GEO angular frequency || 7.29211515e-5 || radians/s || || $ r_{GEO} $ || GEO radius || 42164172.4 || m || || $ v_{GEO} $ || GEO velocity || 3074.66 || m/s || || $ E_{GEO} $ || GEO energy / kg || -14180301.17 || J/kg || || $ H_{GEO} $ || GEO angular momentum/kg || 1.296e11 || m^2^/s || || $ r_p $ || perigee radius || 6458137.0 || m || || $ v_p $ || perigee velocity || 10074.5754 || m/s || || $ e $ || eccentricity || 0.64446 || || || $ a $ || semimajor axis || 18164241.20 || m || || $ r_a $ || apogee radius || 29870345.40 || m || || $ v_a $ || apogee velocity || 2178.1800 || m || || $ acc_a $ || apogee radial accel. || 0.2879 || m/s^2 || || $ E_a $ || apogee energy / kg || -15716587.30 || J/kg || || $ H_a $ || apogee ang momentum/kg || 6.506e10 || m^2^/s || || $ \Delta r $ || radius increase || 12293826.96 || m || || $ \Delta v $ || velocity increase || 896.4800 || m/s || || $ \Delta E $ ||radial energy increase/kg|| 1536286.13 || J/kg || |
For the classical ( zero vertical velocity ) tether capture, $ v_R $ = 0 and $ \theta $ = $ \pi $ . We are at apogee. We know three things about the transfer orbit: $ \Large { 1 \over a } ~ = ~ { 2 \over r_p } - { {v_p}^2 \over \mu } ~ = ~ { 2 \over r_a } - { {v_a}^2 \over \mu } $ Conservation of energy $ v_a r_a ~ = ~ v_p r_p $ ` ` Conservation of angular momentum $ v_a ~ = ~ \omega_{GEO} r_a $ ` ` Definition of zero relative transverse velocity, vehicle to tether That is enough to solve for $ r_a $ : $ \Large { { 2 \mu } \over r_p } - \left( { { \omega_{GEO} {r_a}^2 } \over r_p } \right)^2 ~ = ~ { { 2 \mu } \over r_a } - { \omega_{GEO} {r_a}^2 } $ Which can be reduced to the following iterator: $ r_a \Large = \left( { { 2 \mu } \over { {\omega_{GEO}}^2 } } \left( { r_p \over { r_a + r_p } } \right) \right)^{ 1 \over 3 } $ Iterate on that for a while. It converges in about 20 steps to high accuracy starting anywhere between 0 and $ r_{GEO} $, but slightly faster starting at $ 0.7*r_{GEO} $ If we rendezvous with a hanging tether at the radius $ r_a $, we will have zero velocity vertically and horizontally with respect to the tether, and a small acceleration downwards. We can clamp on and hang at the end of the tether. Our small residual weight will accelerate the tether down, slightly, and launch strain waves up it.v But we aren't done! We need to do two more things - climb up the tether, and restore momentum to the tether. Assume the tether is massive compared to a vehicle, so it does not deflect much. The tether will slow down by a tiny amount, and we must restore the momentum, perhaps with rocket engines. We must also supply energy to lift the vehicle up the tether against the small gravity (minus centrifugal force) at that high altitude. ||<-9:> '''Classical Tether Capture''' || || $ \mu $ || gravitational parameter || 3.986004418e14 || m^3^/s^2^ || || $ \omega_T $ || GEO angular frequency || 7.29211515e-5 || radians/s || || $ r_{GEO} $ || GEO radius || 42164172.4 || m || || $ v_{GEO} $ || GEO velocity || 3074.66 || m/s || || $ E_{GEO} $ || GEO energy / kg || -14180301.17 || J/kg || || $ H_{GEO} $ || GEO angular momentum/kg || 1.296e11 || m^2^/s || || $ r_p $ || perigee radius || 6458137.0 || m || || $ v_p $ || perigee velocity || 10074.5754 || m/s || || $ e $ || eccentricity || 0.64446 || || || $ a $ || semimajor axis || 18164241.20 || m || || $ r_a $ || apogee radius || 29870345.40 || m || || $ v_a $ || apogee velocity || 2178.1800 || m || || $ acc_a $ || apogee radial accel. || 0.2879 || m/s^2 || || $ E_a $ || apogee energy / kg || -15716587.30 || J/kg || || $ H_a $ || apogee ang momentum/kg || 6.506e10 || m^2^/s || || $ \Delta r $ || radius increase || 12293826.96 || m || || $ \Delta v $ || velocity increase || 896.4800 || m/s || || $ \Delta E $ ||radial energy increase/kg|| 1536286.13 || J/kg || |
| Line 131: | Line 191: |
| If we haul the payload up with a solar cell power source weighing as much as the payload, then our "hauling power" will be about (16/2) = 8 watts per kilogram using current satellite technology. Against a 0.2879 m/s^2^ acceleration field, we can move at (8/0.2879) = 28 m/s near the bottom, faster near the top. At 8 watts per kilogram, and 1536286 joules per kilogram, climbing the tether will require at least 53 hours. However, at some point we are velocity limited - perhaps 200m/s for our motor. That occurs when the acceleration force is ( 8/200 ) = 0.04 m/s^2^, about 39800 km high. The velocity limit increases climber time to 55 hours . | If we haul the vehicle up with a solar cell power source weighing as much as the payload, then our "hauling power" will be about (16/2) = 8 watts per kilogram using current satellite technology. Against a 0.2879 m/s^2^ acceleration field, we can move at (8/0.2879) = 28 m/s near the bottom, faster near the top. At 8 watts per kilogram, and 1536286 joules per kilogram, climbing the tether will require at least 53 hours. However, at some point we are velocity limited - perhaps 200m/s for our motor. That occurs when the acceleration force is ( 8/200 ) = 0.04 m/s^2^, about 39800 km high. The velocity limit increases climber time to 55 hours . |
| Line 137: | Line 197: |
| ---- |
|
| Line 141: | Line 203: |
| The capture radius $ r_c $ is below orbit apogee by some as-yet undefined amount. The angular velocity will be $ \omega_T $ as before, so the transverse velocity will be $ \omega_T r_c $. The total velocity squared will be the sum of the squares: $ {v_{vc}}^2 + ( \omega_T r_c )^2 $. $ \omega_T r_c ~ = ~ v_0 ( 1 + e \cos( \theta ) ) $ $ v_{vc} ~ = ~ v_0 e \sin( \theta ) $ $ r_c ~ = ~ r_0 / ( 1 + e \cos( \theta ) ) $ So: $ \sin( \theta ) ~ = ~ { \Large { v_{vc} \over { v_0 e } } } $ $ ~ ~ ~ ~ ~ ~ ~ ~ = ~ { \Large { v_{vc} \over { v_p - \mu / r_p v_p } } } $ $ \cos( \theta ) ~ = ~ - \sqrt{ 1 - \sin( \theta )^2 } $ ` ` . . . Note the quadrant! $\theta$ is near $\pi$, not 0! $ ~ ~ ~ ~ ~ ~ ~ ~ = ~ - \sqrt{ 1 - { \Large \left( { v_{vc} \over { v_p - \mu / r_p v_p } } \right) } ^2 } $ $ \omega_T ~ = ~ ( v_0 / r_0 ) ( 1 + e \cos( \theta ) )^2 $ $ ~ ~ ~ ~ ~ ~ = ~ { \Large { \mu^2 \over { {r_p}^3 {v_p}^3 } } } ~ \left( 1 - \left( { \Large { { r_p {v_p}^2 } \over \mu } } - 1 \right) \sqrt{ 1 - { \Large \left( { v_{vc} \over { v_p - \mu / r_p v_p } } \right) } ^2 } \right)^2 $ Let's solve this mess for $ v_p $. We know all the other terms. It will be iterative, as before: $ v_p ~ = ~ \LARGE \sqrt{ { \Large { \mu \over r_p } + } { { { \mu \over r_p } - \sqrt{ \Large \omega_T r_p {v_p}^3 } } \over \sqrt{ 1 - { \left( { v_{vc} \over { v_p - \mu / r_p v_p } } \right) } ^2 } } } $ If $ v_{vc} $ = 0, this reduces to the classical case above. The capture rail is a long way out of the gravity well, so "natural" vertical deceleration of a vehicle is small. However, there will be some drag from eddy currents in the thin and rather resistive rail. In a production system, the drag profile will be optimized and rather complex. For this analysis, we will just compute the kinetic energy lost by moving up the rail, multiply that by a drag factor, and use that to compute the kinetic energy and velocity left as we approach the dock at GEO. |
The capture radius $ r_c $ is below orbit apogee, and below the GEO altitude . This is a good starting point. The angular velocity will be $ \omega_T $ as before, so the transverse velocity will be: $ v_{tc} = \omega_T r_c $ and the angular momentum is $ h = \omega_T {r_c}^2 $ We know that at launch, at perigee, the angular momentum is the same, so: $ v_p = h / r_p $ We can define the orbit from there, computing $ a $, $ e $, $ v_0 $, $ r_0 $, and $ \theta $ from the equations above. Most interesting is computing the vertical velocity at capture, $ v_{rc} $: $ v_{rc} ~ = ~ \sqrt{ 2 \mu { \Large \left( { 1 \over r_p } - { 1 \over r_c } \right) } + {v_p}^2 - {v_{tc}}^2 } $ Also the vertical energy per mass needed to climb up the tether,$ E_{cc} $: $ E_{cc} ~ = ~ { 1 \over 2 } {\omega_T}^2 \left( {r_c}^2 - {r_{GEO}}^2 \right) + \mu { \Large \left( { 1 \over r_c } - { 1 \over r_{GEO} } \right) } $ If the eddy current losses are negligible ( which requires a thick and heavy conductor track ), then the vehicle will reach (or pass) GEO if $ E_{cc} < { 1 \over 2 } {v_{rc}}^2 $ If we define the capture parameter $ c \equiv r_c / r_{GEO} $ and the perigee parameter $ p \equiv r_p / r_{GEO} \approx $ 0.1531665 then the inequality can be massaged into: $ c^5 - 2 p^2 c^3 + ( 2 p^2 + p ) c - 2 p^2 > 0 $ MORE LATER - that does not look right, yet. The next few bits may be invalid, too The capture rail is a long way out of the gravity well, so "natural" vertical deceleration of a vehicle is small. However, there will be some drag from eddy currents in the thin and rather resistive rail. In a production system, the drag profile will be optimized and rather complex. For this analysis, we will just compute the kinetic energy lost by moving up the rail, multiply that by a drag factor, and use that to compute the kinetic energy and velocity remaining as we approach the dock at GEO. |
| Line 195: | Line 263: |
| ||<-4:> '''GEOrail Tether Capture''' || || $ v_{vc} $ || Vertical V || 2700.0000 || m/s || || $ acc_s $ || slowdown deceleration || 5.0000 || m/s^2^ || || $ D $ || drag factor || 2.0000 || || || $ \mu $ || gravitational parameter || 3.9860E+14 || m^3^/s^2^ || || $ \omega_T $ || GEO angular frequency || 7.2921151E-05 || radians/s || || $ r_{GEO} $ || GEO radius || 42164172.37 || m || || $ v_{GEO} $ || GEO velocity || 3074.6600 || m/s || || $ E_{GEO} $ || GEO energy / kg || -14180301 || J/Kg || || $ H_{GEO} $ || GEO angular momentum/kg || 1.2964E+11 || m^2^/s || || $ r_p $ || perigee radius || 6458137.0 || m || || $ v_p $ || perigee velocity || 10462.7761 || m/s || || $ e $ || eccentricity || 0.77363 || || || $ a $ || semimajor axis || 28529281.45 || m || || $ r_a $ || apogee radius || 50600425.91 || m || || $ v_a $ || apogee velocity || 1335.3651 || m/s || || $ \theta $ || orbit angle at capture || 143.73 || degrees || || $ r_c $ || capture radius || 30440398.47 || m || || $ v_{tc} $ || capture tranverse velo. || 2219.7489 || m/s || || $ E_c $ || capture energy || 15558098 || J/kg || || $ acc_c $ || capture vert. accel. || 0.2683 || m/s^2^ || || $H_{capture}$|| capture ang. momentum/kg|| 6.7570E+10 || m^2^/s || || $ y_s $ || slowdown run || 177982.60 || m || || $ r_s $ || slowdown radius || 41986189.77 || m || || $ v_s $ || slowdown velocity || 1334.10 || s || || $ t_s $ || slowdown time || 266.82 || s || || || tether climb time || 6604.70 || s || || || Partial orbit time || 18533.41 || s || || || Launch time || 348.76 || s || || || Total time || 7.15 || hours || || $ \Delta v $ || velocity increase || 854.9111 || m/s || || $ \Delta E $ ||radial energy increase/kg|| 1377796.89 || J/kg || || $ \Delta H $ ||radial ang. mom. incr./kg|| 6.2070E+10 || m^2^/s || |
||<-9:> '''GEOrail Tether Capture''' || || $ v_{vc} $ || Vertical V || 2700.0000 || m/s || || $ acc_s $ || slowdown deceleration || 5.0000 || m/s^2^ || || $ D $ || drag factor || 2.0000 || || || $ \mu $ || gravitational parameter || 3.9860E+14 || m^3^/s^2^ || || $ \omega_T $ || GEO angular frequency || 7.2921151E-05 || radians/s || || $ r_{GEO} $ || GEO radius || 42164172.37 || m || || $ v_{GEO} $ || GEO velocity || 3074.6600 || m/s || || $ E_{GEO} $ || GEO energy / kg || -14180301 || J/Kg || || $ H_{GEO} $ || GEO angular momentum/kg || 1.2964E+11 || m^2^/s || || $ r_p $ || perigee radius || 6458137.0 || m || || $ v_p $ || perigee velocity || 10462.7761 || m/s || || $ e $ || eccentricity || 0.77363 || || || $ a $ || semimajor axis || 28529281.45 || m || || $ r_a $ || apogee radius || 50600425.91 || m || || $ v_a $ || apogee velocity || 1335.3651 || m/s || || $ \theta $ || orbit angle at capture || 143.73 || degrees || || $ r_c $ || capture radius || 30440398.47 || m || || $ v_{tc} $ || capture tranverse velo. || 2219.7489 || m/s || || $ E_c $ || capture energy || 15558098 || J/kg || || $ acc_c $ || capture vert. accel. || 0.2683 || m/s^2^ || || $H_{capture}$|| capture ang. momentum/kg|| 6.7570E+10 || m^2^/s || || $ y_s $ || slowdown run || 177982.60 || m || || $ r_s $ || slowdown radius || 41986189.77 || m || || $ v_s $ || slowdown velocity || 1334.10 || m/s || || $ t_s $ || slowdown time || 266.82 || s || || || tether climb time || 6604.70 || s || || || Partial orbit time || 18533.41 || s || || || Launch time || 348.76 || s || || || Total time || 7.15 || hours || || $ \Delta v $ || velocity increase || 854.9111 || m/s || || $ \Delta E $ ||radial energy increase/kg|| 1377796.89 || J/kg || || $ \Delta H $ ||radial ang. mom. incr./kg|| 6.2070E+10 || m^2^/s || |
| Line 247: | Line 299: |
MORE LATER |
MORE LATER == M288 capture rail == A similar rail system can supply the M288 [[ http://server-sky.com | server sky orbits ]]. {{ attachment:cap14.png | | width=960, height=320 }} [[ attachment:cap14.c | Here is the source ]] , and you will need [[ http://www.libgd.org/ | libGD ]] and [[ http://apngasm.sourceforge.net/apngasm | apngasm ]]. ||<-9:> '''M288 rail Tether Capture''' || || $ v_{vc} $ || Vertical V || 2933.86 || m/s || || $ acc_s $ || slowdown deceleration || 4.9836 || m/s^2^ || || $ \omega_T $ || M288 angular frequency || 4.37527e-04 || radians/s || || $ r_{M288} $ || M288 radius || 12769564 || m || || $ v_{M288} $ || M288 velocity || 5587.028 || m/s || || $ E_{M288} $ || M288 energy / kg || -15.607e+06 || J/Kg || || $ H_{M288} $ || M288 angular momentum/kg|| 7.1344E+10 || m^2^/s || || $ r_p $ || perigee radius || 6458137.0 || m || || $ v_p $ || perigee velocity || 9603.4591 || m/s || || $ e $ || eccentricity || 0.49426 || || || $ a $ || semimajor axis || 1276564 || m || || $ r_a $ || apogee radius || 19080992 || m || || $ v_a $ || apogee velocity || 3250.3790 || m/s || || $ \theta $ || orbit angle at capture || 112.54 || degrees || || $ r_c $ || capture radius || 11905978.35 || m || || $ v_{tc} $ || capture tranverse velo. || 5209.1859 || m/s || || $ E_c $ || transfer orbit energy || -15.607e+07 || J/kg || || $ acc_c $ || capture vert. accel. || -0.5328 || m/s^2^ || || $H_{capture}$|| capture ang. momentum/kg|| 6.2020E+10 || m^2^/s || || $ y_s $ || slowdown run || 863.59 || km || || || Partial orbit time || 2157.42 || s || || || Launch time || 304.42 || s || || || Total time || 50.84 || minutes || || $\Delta H$ || ang. momentum change/kg || 6.2020E+10 || m^2^/s || With a capture radius of 12769km, and an elliptical orbit with the same semi-major axis the same as the M288 orbit, a miss will result in another capture opportunity one orbit (about 4 hours) later, plus or minus drag in the upper atmosphere. We may choose to add some apogee velocity, and otherwise adjust the orbit so perigee is above the high drag portion of the atmosphere. The M288 orbit is low enough and the magnetosphere particle density is high enough that we can use electrodynamic tether acceleration to restore angular momentum after a capture. 9.3235e9 m^2/s times the angular velocity of 4.375E-4 rad/sec is the energy we need to add back to the tether, about 5 MJ/kg at 80% thrust efficiency. With 16 W/kg solar cells at 62% availability (tilting to the terminator to avoid night sky illumination), 1 kg of solar cells can generate 5MJ in less than 6 days Vertical deltaV could be a problem, but this velocity is tangential to the orbit, doesn't change the capture rail semimajor axis much, and is as likely to add as subtract from radial velocity, depending on where on the capture rail orbit it is added. By timing our launches, we can manage the average towards zero. || || || || || || || || || Angular || || slowdown || || || retry || retry || || || slowdown || Restore || || distance || total || energy || orbit || sidereal || launch || capture || accel || Energy || || km || minutes || ratio || hours || orbits || m/s || m/s || m/s2 || J/kg || || 863.59 || 50.84 || 19.1703 || 3.99 || 1.0000 || 9132.52 || 2933.86 || 4.98 || 4.08E+6 || || 631.83 || 42.86 || 57.5671 || 11.97 || 1.5000 || 9510.04 || 3695.37 || 10.81 || 3.01E+6 || || 507.13 || 39.81 || 109.132 || 7.98 || 2.0000 || 9716.17 || 4069.73 || 16.33 || 2.43E+6 || || 371.80 || 37.09 || 245.410 || 11.97 || 3.0000 || 9942.27 || 4457.78 || 26.72 || 1.79E+6 || MORE LATER == M288 rail bases for orbital debris capture == Server sky thinsats are cheaper to launch if they are lighter, but below a minimum mass-to-area ratio, the orbits are unstable under light pressure. However, we can add mass ballast to a very light satellite, using gram-weight chunks of space debris. The processing is simple, just let the debris shatter as it is collision-captured inside a cornucopia-shaped funnel. Larger chunks can be cut apart at a simple processing plant at the M288 rail base, smaller chunks can be welded together. Capture vehicles can drop below the tether, in intercept orbits where the debris crosses the equatorial plane. Depending on their orbit, they can return to the same rail base, but more likely a different rail base will be more convenient. MORE LATER |
Capture Rail
"Landing" Launch Loop payloads on tethers in circular orbit, without apogee kick motors
More rockets bite the dust ...
The launch loop provides low cost delta-V from the earth's surface, injecting vehicles into highly elliptical transfer orbits, or earth-escape orbits. What a launch loop cannot do directly is put a payload into a circular orbit. The perigee of a launch-loop launch will always be at the launch track height, even if the apogee reaches the moon. To put a vehicle into a higher circular orbit requires additional angular momentum, usually supplied by a rocket.
Tethers provide an alternative. A zero-velocity capture on a vertical tether means that the launch loop launches payloads with an angular velocity matching that of the tether, at a lower altitude ( or radius ) than the center of the tether's orbit.
Classic Tether Capture
Yellow is a vehicle in a transfer orbit from launch. Green is a capture, red is a missed capture.
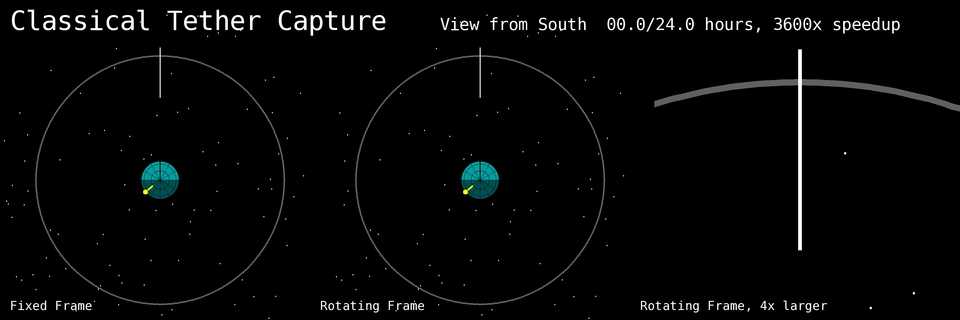
Here is the source , and you will need libGD and apngasm.
Capturing on a tether is not a new idea. The transfer orbit is chosen such that the vehicle arrives at the tether with zero velocity, and clamps on. It will have a small relative acceleration downwards, perhaps 2.5% of one gee, a fairly light load, assuming the tether is much more massive than the vehicle.
There are problems with classic tether capture. For a tether in geostationary orbit, capturing a vehicle in a transfer orbit with a perigee of 80km, the capture radius (the apogee of the transfer orbit) is at 29870 km, 12294 km below the geostationary altitude of 42164 km. Somehow, the vehicle must climb up the tether for more than 12000 kilometers. With the very small gee loading, this is not nearly as difficult as climbing up a space elevator from the Earth's surface, and a tractor vehicle can be waiting on the tether to pull up the launch vehicle. However, with limited power and wheel velocity, this will still take a while. At 200 kilometers per hour, the climb will take 61 hours. The climb will probably be slower on the higher gee lower section.
We will be stealing angular momentum from the tether, so we will need something like a VASIMR electric rocket to add the momentum again.
Worse still, what if we miss the capture? The period of the circular transfer orbit is 6.768 hours; the next time the vehicle reaches apogee, the tether will be a long way away, and we may need many days and hundreds of meters per second of delta V to catch it again.
Climbing Tether Capture

Here is the source, and you will need libGD and apngasm.
But who says the vehicle is constrained to zero vertical/radial velocity?
Vehicles leave the launch loop with a magnetic rail attached to the bottom, which magnetically drags on the rotor and propels them to orbital speeds. The magnetic rail is passive - it can only produce drag - but it can drag on anything conductive, such as a very thin metal tube around a tether. If we arrive at the tether with zero transverse/horizontal velocity, and a high radial/vertical velocity, we can ride the magnetic rail, just like the launch loop track that we left a few hours before. As we ride up the rail, we slow down against it. In a matter of minutes, we brake to a stop at geostationary radius. This requires a few percent more deltaV at launch, but launch velocity is cheap with a launch loop.
Transit time from start of launch to arrival at GEO will be less than 4 hours. The transit time will be slightly faster than a classic Hohmann transfer orbit with an apogee kick motor.
Other benefits include a somewhat shorter hanging tether, which also reduces the amount of angular momentum the vehicle removes from the tether.
For a geostationary target orbit, we can choose a transfer orbit with a 12 hour period and a semimajor axis of 26562 km (0.62996 smaller semimajor axis than the 42164 km GEO orbit). If apogee remains at launch loop exit altitude (6458 km), then drag can help the vehicle reenter 12 hours later, on the other side of the earth from the launch loop. It we instead choose to make another try, we can add 10m/s deltaV at apogee, and raise perigee by 45 km, a 200x reduction in drag. That will give us one or two more passes at capture, 24 and 48 hours later. The unmodified orbit is the "12 hour low" orbit, while the boosted perigee orbit is the "12 hour high" orbit. Actually, we must also perform a second burn at perigee, to lower apogee, if we wish to maintain the same semimajor axis and the same 12 hour orbit period.
We can also choose a transfer orbit with a 24 hour complete period, and perform the same perigee-raising maneuver if we wish to reduce drag and make a second pass. That higher orbit will have higher angular momentum, and draw less angular momentum from the tether.
Transfer Orbit |
Perigee |
Apogee |
VP |
VA |
AngM |
Rcapture |
|
km |
km |
m/s |
m/s |
m2/s |
km |
12 hour low |
6458 |
46665 |
|
|
|
|
12 hour high |
6503 |
46620 |
||||
24 hour low |
6458 |
77870 |
||||
24 hour high |
6503 |
77825 |
A 24 hour orbit, geostationary capture tether, fed from a fixed point on earth, is perhaps the easiest capture tether to imagine. However, a non-synchronous capture tether offers more flexibility, as we will see below.
THE REST OF THIS PAGE WILL BE REWORKED
Imagine a long and heavy orbiting tether, running vertically from 29000 km radius, through GEO (42164 km), to a counterweight above. The tether has a thin, passive conductive rail around it. It will be used to magnetically capture vehicles and move them to GEO, using the sliding rail to push payloads transversely while they magnetically slide upwards.
This is not the normal apogee capture system, where we launch into an orbit whose perigee transverse velocity matches a hanging tether at the right altitude. Instead, we launch the vehicle a little faster and a little later. That puts the vehicle in an orbit with an apogee trailing the tether. The vehicle will never get to that apogee, because we will slide in front of the tether below apogee, where we still have a high (2700 m/s) radial velocity. We will still match the tether's transverse velocity and altitude, though.
In the rotating tether frame of reference, the vehicle will approach from below at high speed, from the rear, and decelerate in the traverse ("horizontal") direction as it approaches the tether. The vehicle is rising radially, conserving angular momentum, and losing angular velocity as the radius increases. In the tether's rotating frame, this looks like Coriolis acceleration, equal to twice the velocity times the tether's angular velocity. The angular orbital velocity for a GEO tether is 7.2921E-5 radians per second, and the radial ("vertical") velocity will be around 2700 meters per second, so the Coriolis acceleration is 0.27 m/s2. If the vehicle misses the tether rendezvous, it will continue to accelerate retrograde in the rotating frame, with the backwards velocity turning into downwards Coriolis acceleration in the rotating frame, reaching apogee above the intended attach point but well below GEO.
The tether is made with not-excessively-tapered Kevlar. We will need many tons of it, especially at GEO, as an angular momentum bank. More mass is better for this system. THIS is where we put the hotels, the radiation shielding, and the heavy buffet tables for obese tourists.
We launch a vehicle off the launch loop at 10463 m/s, and with very good radar and some trim thrusters, we "land" on the bottom of the rail at 30440 km altitude. At that point, we have the same angular frequency and circular orbital velocity, and a large vertical velocity component, 2700 m/s .
As the vehicle slides up the tether, the weak gravity and eddy current drag slows it down radially, as it accelerates transversely (forwards) in orbit to remain on the "faster at higher altitude" tether.
As the vehicle slides upwards, it magnetically levitates/pushes against the east side of the rail with Coriolis acceleration. That is 39 centimeters per second squared at 2700 m/s vertically, and 19 centimeters per second squared at 1334 m/s, our speed as we approach GEO altitude. The Coriolis acceleration and the eddy currents both reduce with relative velocity - most convenient! The vertical deceleration (gravity minus rotational centrifugal acceleration) decreases to zero as we approach GEO, still with significant velocity, though with less than the velocity of a frictionless ballistic because of the eddy currents.
As the vehicle approaches GEO, it is still moving fast, which is good, because it has 12000 kilometers to travel. The trip will take about 5 hours from earth, and 2 hours riding up the tether. It will be slower than a Hohmann with an apogee kick motor, but much cheaper and less polluting. At "slowdown height", about 180 kilometers below GEO station, the rail surface changes to increase eddy current drag, slowing down the vehicle. The vehicle reaches the drag section at 1334 meters per second, and deceleration increases from a few millimeters per second to 5 m/s2, a bit more than half a gee (with passengers facing backwards, backs into chairs). The vehicle slows to 25 meters per second about 40 meters below the station, and with active track control, reduces deceleration and velocity to zero over the next 5 seconds. The payload or passenger compartment is plucked off the magnet-rail and wing, and pushed into the station through an airlock.
Since the tether rail is not magnetic or active (that would be far too heavy for a 12000 kilometer gossamer structure) the vehicle magnet-rail will need to wrap partly around it in some way. 39 cm/s2 Coriolis acceleration is far too weak to hold the vehicle against a rippling tether at high speed. For example, a ripple with a 20 kilometer wavelength and a 20 meter peak-to-peak amplitude will shake the vehicle back and forth at 0.8 gees ( 12x Coriolis ) and a period of 7 seconds - a frisky roller coaster. Such a transverse ripple will not be a standing wave, but traveling up or down the tether at around 1 km per second. It will be a challenge to remove it, perhaps by periodic transverse shaking at GEO by the large momentum mass. It would be more difficult to remove by shaking the bottom counterweight vertically, inducing Coriolis accelerations, because a lot of power is required.
We can reverse the process. Using a magnetic accelerator to launch a vehicle down a rail on the west side of the tether, we falling off the end in a transfer orbit back to the upper atmosphere. This restores most of the GEO rail momentum.
The rocket thrust needed by GEO rail vehicles will be pure velocity correction, centimeters per second if we've done our radar and orbital mechanics calculations correctly. If we miss, we just reenter normally - a delay, but not a disaster. Besides a little correction exhaust, and whatever we need to add to for momentum restoration, the system is mass conservative and mostly energy-recycling.
Restoring GEO Rail orbital momentum
If we de-orbit GEO station trash much faster than we receive payloads (aiming for empty and lifeless portions of the ocean) we can add more momentum by exploiting Coriolis force acceleration. We can also receive mass (and momentum) from the moon, or launch mass from the loop in slingshot orbits around the moon. However, the moon will not always be conveniently located for this, and vehicles may make many 20 day orbits before arriving with a suitable orbital position.
A slightly stronger tether can swing like a pendulum. That allows vehicles to arrive from the launch loop with higher angular velocity, and leave with lower angular velocity. This variation needs further study.
VASIMR and "Zero Orbiting Exhaust" momentum restoration
We will probably need to make up some energy and momentum losses with plasma rocket engines at GEO station, especially if we accumulate more upward vehicles than downward ones. But overall, the energy will be tiny compared to the the launch loop energies, and we can float a lot of solar cell around GEO as part of our "momentum anchor".
As part of an overall "space anti-litter" ethic, we should make sure the plasma rocket engines are offset so they are firing exhaust away from the rest of the geosynchronous ring, and that the rocket exhaust is traveling fast enough to escape the solar system ( >16 km/sec at noon when the rockets are pushing retrograde to the Earth's orbit around the sun, >76 km/sec (!!) at midnight, when the rockets are pushing retrograde ).
A Variable Specific Impulse Magnetoplasma Rocket (VASIMR) engine operates optimally at 50 km/sec, so operation at 80 km/sec is close to optimum. The reaction mass is argon, which can be frozen at -200C with a density of 1600 kg/m3 and a vapor pressure of 0.1 atmosphere for transit from earth. We will need about 1 kg of argon reaction mass shipped up for every 50 kg of uncompensated mass shipped up from Earth. Argon is 0.93% of the atmosphere, and costs about $1/kg (liquid) in large quantities. It is a byproduct of liquid oxygen production.
With 80km/s exhaust, we will expend about 40 kilowatt hours per "uncompensated vehicle kilogram" operating the plasma rockets, including coolers and radiator operation. Typical solar cell weights for existing satellites are 65 kg/kilowatt, or 16 watts per kilogram, so 1 kilogram of solar cells provides enough energy in a year to bring aboard 3.5 kilograms of mass - a power doubling time of 5 months. However, if we can use "server sky" style ultra-thin InP cells, closer to 1000 kg/kW, we can approach 50 kilograms of mass per kilogram-year of solar cell. In the very long term, solar cells made from lunar materials will bring both momentum and cheaper launch to the GEO rail, but solar cells are a high-tech undertaking, and it will be a long time before that level of manufacturing technology exists in space.
In the shorter term, perhaps there is some variant of VASIMR that can operate at lower exhaust velocities, expending more argon but using less energy. If we fire the argon out at 4500 m/s, and don't have too much thermal spread, the argon will be in a ballistic orbit that falls into the atmosphere (returning the argon where we found it). This will require 1 kilogram of argon for every 3 kilograms of payload shipped, which may mean that every other payload is argon during construction. However, at 50% efficiency, and 50% mass fraction we will need only 3.8 kW-hours of energy per kilogram of incoming non-argon mass, resulting in 1 kg per 10 kg-days of solar cell. That will lead to very fast growth rates of the power and engine systems, rapidly evolving towards the high velocity exhaust scenario.
The above analysis assumes that the argon plasma neutralizes - if it stays ionized, it will gyrate in the Earth's magnetic field and not go much of anywhere, because the pitch angle will be high. That will be interesting, perhaps the trapped particles will act as shielding mass against higher energy particles trapped on the same field lines, but that analysis must wait for another time.
Also - do not assume that we can fire the argon at night at just the right velocity so that the exhaust falls into the sun. The sun is a small target, and distant, so with thermal spread much of the exhaust will end up in highly elliptical orbits that reach earth's orbit. The gas will be dilute, and most of it that returns will collect in the morning sky, but it will add some pollution in the long run.
How much argon will we use? The Earth's atmosphere weighs 5E15 tons, and about 1% is argon, so 5E13 tons of argon are available. With 80km/s exhaust resulting in a 50:1 payload-to-argon ratio, we can ship up 2.5E15 tons before we run out of argon. Chances are, we will be shipping down material and momentum from the moon long before we make a dent in the argon supply.
Conductor Track Weight
Assume a 5 ton vehicle moving at 2700m/s with 1.0 m/s2 transverse acceleration (lots of vibration!), and 0.3 m/s2 radial deceleration from the magnetic field. The total transverse force is 5000N, the deceleration force is 1500N. The deceleration power is 4MW .
Assume a 10 meter magnet rail with 0.2T undulating fields and 50% fill, and an average of 4 cm of "track width" on a 6cm diameter aluminum tube (bonded to a Kevlar core tube), so the "bearing surface" is 0.2 m2. The field pressure is 5000N/0.2m2 or 25000N/m2, which is 0.2T times 125,000 amps per meter in the conductor. Assume the current path is effectively 10cm long and 5 meters wide for 625KA total. For a deceleration power of 4MW, the resistance of the current path must be 4MW/(625KA2) or 10 micro-ohms. The resistivity per square of the aluminum will be (5.0/0.1) times that, or 500 micro-ohms per square. Aluminum is about 30 nano-ohm-meter, so a thickness of 60 microns will have that resistivity. The cross section is pi * 0.06m * 6E-5m or 1.13E-5 m2, for a mass per meter of 30 grams (aluminum density is 2.7). That is 30kg/km, or 360 tons of aluminum for the whole 12000 km track.
4MW/2700m/s, or 1500 Joules per meter of heat energy will be deposited into the 30g/m track. Aluminum heat capacity is 0.9 J/gm-K, so it could heat by about 56K. However, it is bonded to a much larger mass of Kevlar (1.4 J/gm-K), and the thermal diffusion time through 60 microns of aluminum is about 40 microseconds. The 10 meter magnet rail passes by in 3.7 milliseconds, so we can assume that most of the heat has passed into the Kevlar core, and the aluminum heats much less.
MORE LATER
The Math
We will neglect oblateness, light pressure, and the gravity of other bodies for now. Simple Kepler two body orbits around the earth.
The vehicle leaves the launch loop at 80km altitude, the apogee of an elliptical orbit with a perigee of r_p = 6458.137 km and velocity v_a . The earth's gravitational parameter \mu = 398600.4418 km3/s2 = 3.986004418e14 m3/s2. Given those three values, we define the orbit:
h ~ = ~ r_p v_p angular momentum
a ~ = ~ { \Large { 1 \over { \LARGE { 2 \over r_p } ~ - ~ \LARGE { { {v_p}^2 } \over { \huge \mu } } } } } semi-major axis
e ~ = ~ 1 - { \Large { { r_p } \over a } } ~ = ~ { \Large { { r_p {v_p}^2 } \over \mu } } - 1 eccentricity
v_0 ~ = ~ { \Large { { v_p } \over { 1 + e } } } ~ = ~ { \Large { { \mu } \over { r_p v_p } } } characteristic velocity
r_0 ~ = ~ a ( 1 - e^2 ) ~ = ~ \Large { { {r_p}^2 {v_p}^2 } \over \mu } characteristic radius
r( \theta ) ~ = ~ \Large { r_0 \over { 1 + e \cos( \theta ) } } orbit radius as a function of \theta , the angle from perigee or true anomaly
{v_T}( \theta ) ~ = ~ v_0 ( 1 + e \cos( \theta ) ) orbit transverse velocity
{v_R}( \theta ) ~ = ~ v_0 e \sin( \theta ) orbit radial velocity
{\omega } ( \theta ) ~ = ~ { \Large { h \over{ r^2 } } } ~ = ~{ \Large { { \mu^2 ( 1 + e \cos( \theta ) )^2 } \over { {r_p}^3 {v_p}^3 } } } orbit angular velocity
r_a ~ = ~ ( 1 + e ) a ~ = ~ { \Large 1 \over { \LARGE { { \huge 2 \mu } \over { r_p {v_p}^2 } } ~ - ~1 } } apogee
The angular velocity of the tether in geostationary orbit (defined by the stellar day ) is \omega_T = 2 \pi / 86164.098903691 = 7.29211515E-5 radians per second.
At the capture point, the orbit has the same angular velocity as the tether, \omega = \omega_T .
Classical Tether Capture
For the classical ( zero vertical velocity ) tether capture, v_R = 0 and \theta = \pi . We are at apogee.
We know three things about the transfer orbit:
\Large { 1 \over a } ~ = ~ { 2 \over r_p } - { {v_p}^2 \over \mu } ~ = ~ { 2 \over r_a } - { {v_a}^2 \over \mu } Conservation of energy
v_a r_a ~ = ~ v_p r_p Conservation of angular momentum
v_a ~ = ~ \omega_{GEO} r_a Definition of zero relative transverse velocity, vehicle to tether
That is enough to solve for r_a :
\Large { { 2 \mu } \over r_p } - \left( { { \omega_{GEO} {r_a}^2 } \over r_p } \right)^2 ~ = ~ { { 2 \mu } \over r_a } - { \omega_{GEO} {r_a}^2 }
Which can be reduced to the following iterator:
r_a \Large = \left( { { 2 \mu } \over { {\omega_{GEO}}^2 } } \left( { r_p \over { r_a + r_p } } \right) \right)^{ 1 \over 3 }
Iterate on that for a while. It converges in about 20 steps to high accuracy starting anywhere between 0 and r_{GEO} , but slightly faster starting at 0.7*r_{GEO}
If we rendezvous with a hanging tether at the radius r_a , we will have zero velocity vertically and horizontally with respect to the tether, and a small acceleration downwards. We can clamp on and hang at the end of the tether. Our small residual weight will accelerate the tether down, slightly, and launch strain waves up it.v
But we aren't done! We need to do two more things - climb up the tether, and restore momentum to the tether. Assume the tether is massive compared to a vehicle, so it does not deflect much. The tether will slow down by a tiny amount, and we must restore the momentum, perhaps with rocket engines. We must also supply energy to lift the vehicle up the tether against the small gravity (minus centrifugal force) at that high altitude.
Classical Tether Capture |
||||||||
\mu |
gravitational parameter |
3.986004418e14 |
m3/s2 |
|
\omega_T |
GEO angular frequency |
7.29211515e-5 |
radians/s |
r_{GEO} |
GEO radius |
42164172.4 |
m |
|
v_{GEO} |
GEO velocity |
3074.66 |
m/s |
E_{GEO} |
GEO energy / kg |
-14180301.17 |
J/kg |
|
H_{GEO} |
GEO angular momentum/kg |
1.296e11 |
m2/s |
r_p |
perigee radius |
6458137.0 |
m |
|
v_p |
perigee velocity |
10074.5754 |
m/s |
e |
eccentricity |
0.64446 |
|
|
a |
semimajor axis |
18164241.20 |
m |
r_a |
apogee radius |
29870345.40 |
m |
|
v_a |
apogee velocity |
2178.1800 |
m |
acc_a |
apogee radial accel. |
0.2879 |
m/s^2 |
|
E_a |
apogee energy / kg |
-15716587.30 |
J/kg |
H_a |
apogee ang momentum/kg |
6.506e10 |
m2/s |
|
\Delta r |
radius increase |
12293826.96 |
m |
\Delta v |
velocity increase |
896.4800 |
m/s |
|
\Delta E |
radial energy increase/kg |
1536286.13 |
J/kg |
\Delta H |
radial ang. mom. incr./kg |
6.458e10 |
m2/s |
|||||
If we haul the vehicle up with a solar cell power source weighing as much as the payload, then our "hauling power" will be about (16/2) = 8 watts per kilogram using current satellite technology. Against a 0.2879 m/s2 acceleration field, we can move at (8/0.2879) = 28 m/s near the bottom, faster near the top. At 8 watts per kilogram, and 1536286 joules per kilogram, climbing the tether will require at least 53 hours. However, at some point we are velocity limited - perhaps 200m/s for our motor. That occurs when the acceleration force is ( 8/200 ) = 0.04 m/s2, about 39800 km high. The velocity limit increases climber time to 55 hours .
If we can use a pulley system without tangling cables, running at 400m/s, climber time is 8.5 hours. We can go a lot faster if we are not moving the motor and the solar cells.
MORE LATER
Rail Tether Capture, with vertical velocity
This is a little trickier. The system moves faster if we have a lousy "lift to drag" ratio, because we can travel the tether faster. It also makes the math a little simpler if we pick a fixed starting speed, as long as it is more than enough to make the climb. Lets start with the energy increase for the classic case, 1.54 MJ/kg , double it, and turn the result into a velocity: about 2500 meters per second. We will arbitrarily choose that as v_{vc} , the vertical speed the vehicle will be moving up the tether when it is captured. Since we are launching from the loop with about 52 MJ/kg anyway, an extra 3% energy loss will not be a show stopper, and we will get to the GEO rail station faster. Time is money!
The capture radius r_c is below orbit apogee, and below the GEO altitude . This is a good starting point. The angular velocity will be \omega_T as before, so the transverse velocity will be:
v_{tc} = \omega_T r_c
and the angular momentum is
h = \omega_T {r_c}^2
We know that at launch, at perigee, the angular momentum is the same, so:
v_p = h / r_p
We can define the orbit from there, computing a , e , v_0 , r_0 , and \theta from the equations above.
Most interesting is computing the vertical velocity at capture, v_{rc} :
v_{rc} ~ = ~ \sqrt{ 2 \mu { \Large \left( { 1 \over r_p } - { 1 \over r_c } \right) } + {v_p}^2 - {v_{tc}}^2 }
Also the vertical energy per mass needed to climb up the tether, E_{cc} :
E_{cc} ~ = ~ { 1 \over 2 } {\omega_T}^2 \left( {r_c}^2 - {r_{GEO}}^2 \right) + \mu { \Large \left( { 1 \over r_c } - { 1 \over r_{GEO} } \right) }
If the eddy current losses are negligible ( which requires a thick and heavy conductor track ), then the vehicle will reach (or pass) GEO if
E_{cc} < { 1 \over 2 } {v_{rc}}^2
If we define the capture parameter c \equiv r_c / r_{GEO} and the perigee parameter p \equiv r_p / r_{GEO} \approx 0.1531665 then the inequality can be massaged into:
c^5 - 2 p^2 c^3 + ( 2 p^2 + p ) c - 2 p^2 > 0
MORE LATER - that does not look right, yet. The next few bits may be invalid, too
The capture rail is a long way out of the gravity well, so "natural" vertical deceleration of a vehicle is small. However, there will be some drag from eddy currents in the thin and rather resistive rail. In a production system, the drag profile will be optimized and rather complex. For this analysis, we will just compute the kinetic energy lost by moving up the rail, multiply that by a drag factor, and use that to compute the kinetic energy and velocity remaining as we approach the dock at GEO.
The vertical deceleration is given by:
acceleration = \omega^2 r - \mu / r^2 . . . zero at GEO, of course!
and the specific energy ( J/kg ) can be computed by integrating that:
E(r) = 0.5 \omega^2 r^2 - \mu / r
The drag factor is D , and will always be greater than 1, so the velocity nearing GEO will be:
v_{GEO} \approx \sqrt{ {v_{vc}}^2 - 2 D ( E_{GEO} - E_{capture} ) }
The velocity at radius r will be:
v(r) \approx \sqrt{ {v_{vc}}^2 + D \omega^2 ( r^2 - {r_c}^2 ) - 2 D \mu ( 1 / r_c - 1 / r ) }
The transit time from the capture point to GEO will be:
time = {\huge\int} _{r_c}^{GEO} { \Large { dr \over {v(r)} } } ... which probably requires numerical integration
Since we want to keep the transit time small, we would like to keep the rail very straight and travel up it quickly. So we keep the drag and deceleration relatively low for most of the trip. As we approach GEO, however, we "hit the brakes", decelerating at a much higher rate, so we come quickly and smoothly to a stop at the dock. The transition from low to high deceleration occurs at the slowdown radius r_s .
Here's a close-to-minimum transit time capture:
GEOrail Tether Capture |
||||||||
v_{vc} |
Vertical V |
2700.0000 |
m/s |
|
acc_s |
slowdown deceleration |
5.0000 |
m/s2 |
D |
drag factor |
2.0000 |
|
|
\mu |
gravitational parameter |
3.9860E+14 |
m3/s2 |
\omega_T |
GEO angular frequency |
7.2921151E-05 |
radians/s |
|
r_{GEO} |
GEO radius |
42164172.37 |
m |
v_{GEO} |
GEO velocity |
3074.6600 |
m/s |
|
E_{GEO} |
GEO energy / kg |
-14180301 |
J/Kg |
H_{GEO} |
GEO angular momentum/kg |
1.2964E+11 |
m2/s |
|
r_p |
perigee radius |
6458137.0 |
m |
v_p |
perigee velocity |
10462.7761 |
m/s |
|
e |
eccentricity |
0.77363 |
|
a |
semimajor axis |
28529281.45 |
m |
|
r_a |
apogee radius |
50600425.91 |
m |
v_a |
apogee velocity |
1335.3651 |
m/s |
|
\theta |
orbit angle at capture |
143.73 |
degrees |
r_c |
capture radius |
30440398.47 |
m |
|
v_{tc} |
capture tranverse velo. |
2219.7489 |
m/s |
E_c |
capture energy |
15558098 |
J/kg |
|
acc_c |
capture vert. accel. |
0.2683 |
m/s2 |
H_{capture} |
capture ang. momentum/kg |
6.7570E+10 |
m2/s |
|
y_s |
slowdown run |
177982.60 |
m |
r_s |
slowdown radius |
41986189.77 |
m |
|
v_s |
slowdown velocity |
1334.10 |
m/s |
t_s |
slowdown time |
266.82 |
s |
|
|
tether climb time |
6604.70 |
s |
|
Partial orbit time |
18533.41 |
s |
|
|
Launch time |
348.76 |
s |
|
Total time |
7.15 |
hours |
|
\Delta v |
velocity increase |
854.9111 |
m/s |
\Delta E |
radial energy increase/kg |
1377796.89 |
J/kg |
|
\Delta H |
radial ang. mom. incr./kg |
6.2070E+10 |
m2/s |
\Delta r |
radius increase |
11723773.89 |
m |
|||||
Here's a table of transit time versus versus vertical capture velocity. The capture velocity is quite sensitive to launch velocity, which must be controlled to mm/sec. Note that if we launch very fast, we spend a long time heading out and coming back to the tether. These are all "drag=2" times; if we reduce drag, the optimum occurs at a lower launch velocity.
Transit time versus vertical tether velocity |
time, seconds |
total |
||||||
vertical |
vp |
a |
rc |
launch |
orbit |
climb |
slow |
hours |
3200.00 |
10615.08 |
37940037 |
30661158 |
354 |
24481 |
4330 |
446 |
8.23 |
3000.00 |
10551.38 |
32915772 |
30569017 |
352 |
21591 |
4991 |
381 |
7.59 |
2800.00 |
10491.37 |
29807595 |
30481967 |
350 |
19422 |
5934 |
308 |
7.23 |
2750.00 |
10476.96 |
29148708 |
30461018 |
349 |
18964 |
6245 |
288 |
7.18 |
2700.00 |
10462.78 |
28529281 |
30440398 |
349 |
18533 |
6605 |
267 |
7.15 |
2650.00 |
10488.83 |
27946160 |
30420112 |
348 |
18129 |
7028 |
244 |
7.15 |
2600.00 |
10435.13 |
27396521 |
30400159 |
348 |
17749 |
7542 |
220 |
7.18 |
2550.00 |
10421.67 |
26877836 |
30380544 |
347 |
17390 |
8193 |
193 |
7.26 |
2500.00 |
10408.45 |
26387830 |
30361268 |
347 |
17053 |
9075 |
162 |
7.40 |
2400.00 |
10382.74 |
25485852 |
30323743 |
346 |
16433 |
13467 |
70 |
8.42 |
There may be another set of optima at much higher launch velocities. If we fire the vehicle off the launch loop very fast, we are shooting it almost straight up the tether. The simulations did not capture that because \theta is less than 90 degrees, the cosine changes sign, and the orbit is probably parabolic with an eccentricity greater than 1. While that might shave off some transit time, if the vehicle misses a capture, it will be lost in interplanetary or even interstellar space.
MORE LATER
M288 capture rail
A similar rail system can supply the M288 server sky orbits.
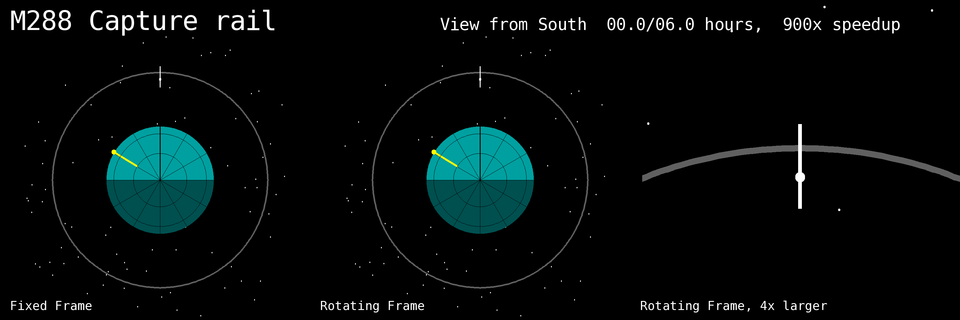
Here is the source , and you will need libGD and apngasm.
M288 rail Tether Capture |
||||||||
v_{vc} |
Vertical V |
2933.86 |
m/s |
|
acc_s |
slowdown deceleration |
4.9836 |
m/s2 |
\omega_T |
M288 angular frequency |
4.37527e-04 |
radians/s |
|
r_{M288} |
M288 radius |
12769564 |
m |
v_{M288} |
M288 velocity |
5587.028 |
m/s |
|
E_{M288} |
M288 energy / kg |
-15.607e+06 |
J/Kg |
H_{M288} |
M288 angular momentum/kg |
7.1344E+10 |
m2/s |
|
r_p |
perigee radius |
6458137.0 |
m |
v_p |
perigee velocity |
9603.4591 |
m/s |
|
e |
eccentricity |
0.49426 |
|
a |
semimajor axis |
1276564 |
m |
|
r_a |
apogee radius |
19080992 |
m |
v_a |
apogee velocity |
3250.3790 |
m/s |
|
\theta |
orbit angle at capture |
112.54 |
degrees |
r_c |
capture radius |
11905978.35 |
m |
|
v_{tc} |
capture tranverse velo. |
5209.1859 |
m/s |
E_c |
transfer orbit energy |
-15.607e+07 |
J/kg |
|
acc_c |
capture vert. accel. |
-0.5328 |
m/s2 |
H_{capture} |
capture ang. momentum/kg |
6.2020E+10 |
m2/s |
|
y_s |
slowdown run |
863.59 |
km |
|
Partial orbit time |
2157.42 |
s |
|
|
Launch time |
304.42 |
s |
|
Total time |
50.84 |
minutes |
|
\Delta H |
ang. momentum change/kg |
6.2020E+10 |
m2/s |
With a capture radius of 12769km, and an elliptical orbit with the same semi-major axis the same as the M288 orbit, a miss will result in another capture opportunity one orbit (about 4 hours) later, plus or minus drag in the upper atmosphere. We may choose to add some apogee velocity, and otherwise adjust the orbit so perigee is above the high drag portion of the atmosphere.
The M288 orbit is low enough and the magnetosphere particle density is high enough that we can use electrodynamic tether acceleration to restore angular momentum after a capture. 9.3235e9 m^2/s times the angular velocity of 4.375E-4 rad/sec is the energy we need to add back to the tether, about 5 MJ/kg at 80% thrust efficiency. With 16 W/kg solar cells at 62% availability (tilting to the terminator to avoid night sky illumination), 1 kg of solar cells can generate 5MJ in less than 6 days
Vertical deltaV could be a problem, but this velocity is tangential to the orbit, doesn't change the capture rail semimajor axis much, and is as likely to add as subtract from radial velocity, depending on where on the capture rail orbit it is added. By timing our launches, we can manage the average towards zero.
|
|
|
|
|
|
|
|
Angular |
slowdown |
|
|
retry |
retry |
|
|
slowdown |
Restore |
distance |
total |
energy |
orbit |
sidereal |
launch |
capture |
accel |
Energy |
km |
minutes |
ratio |
hours |
orbits |
m/s |
m/s |
m/s2 |
J/kg |
863.59 |
50.84 |
19.1703 |
3.99 |
1.0000 |
9132.52 |
2933.86 |
4.98 |
4.08E+6 |
631.83 |
42.86 |
57.5671 |
11.97 |
1.5000 |
9510.04 |
3695.37 |
10.81 |
3.01E+6 |
507.13 |
39.81 |
109.132 |
7.98 |
2.0000 |
9716.17 |
4069.73 |
16.33 |
2.43E+6 |
371.80 |
37.09 |
245.410 |
11.97 |
3.0000 |
9942.27 |
4457.78 |
26.72 |
1.79E+6 |
MORE LATER
M288 rail bases for orbital debris capture
Server sky thinsats are cheaper to launch if they are lighter, but below a minimum mass-to-area ratio, the orbits are unstable under light pressure. However, we can add mass ballast to a very light satellite, using gram-weight chunks of space debris. The processing is simple, just let the debris shatter as it is collision-captured inside a cornucopia-shaped funnel. Larger chunks can be cut apart at a simple processing plant at the M288 rail base, smaller chunks can be welded together.
Capture vehicles can drop below the tether, in intercept orbits where the debris crosses the equatorial plane. Depending on their orbit, they can return to the same rail base, but more likely a different rail base will be more convenient.
MORE LATER
