|
Size: 49
Comment:
|
← Revision 52 as of 2021-06-25 23:48:19 ⇥
Size: 6018
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| #format jsmath | |
| Line 3: | Line 4: |
| [[attachment:CNTE.zip | CNTE.zip ]] | . [[attachment:CNTE.zip | CNTE.zip ]] . . . . [[attachment:FD.zip | FD.zip ]] . . . . [[attachment:NN.zip | NN.zip ]] Pure carbon nanotubes exhibit '''superlubricity''' - approximately ZERO friction between neighboring tubes in a bundle. In 2013, Zhang et. al. published a paper on [[ https://www.researchgate.net/profile/WZ_Qian/publication/258253770_Superlubricity_in_centimetres-long_double-walled_carbon_nanotubes_under_ambient_conditions/links/0046353390b48ed61f000000.pdf | carbon nanotube superlubricity ]] that measured the intershell sliding force of a 1 centimeter long double-wall carbon nanotube (DWCNT), pulling a single inner tube out of a centimeter-long outer tube with an atomic force microscope. Three diameters were measured, and the tiny pullout force matched theory, a function of outer tube diameter. [[ http://oatao.univ-toulouse.fr/4770/1/Laurent_4770.pdf | Laurent et. al. ]] estimates that the inner tube diameter is 0.34nm ( $ d_{s-s} $ ) less than the outer tube diameter, and that DWCNT density (g/cm³) is: $ \rho_{MW} = 6084 g/cm³ { \Large { ( d_{out} ~ - ~ d_{s-s} ) \over { d_{out}^2 } } } $ with $ d_{s-s} = 0.34nm $ and $ d_{out} $ in nanometers. I added my own estimations for perfect hexagonally close packed tube density, tubes/m² $ = \sqrt( 3 ) / 2 D^2 = 0.866 / D^2 $ The pullout pressure $ P = 866 F / D^2 $ MPa if F is nanonewtons and D is nanometers. Results: ||<-2> Zhang et. al. || ||<-2> Laurent et. al || || Diameter || Pullout || || Inner || Density || Tubes || Pullout || Strength || || nm || Force nN || || nm || kg/m³ || / m² || Pressure || Kyuri || || 2.73 || 1.37 || || 2.39 || 1951 || 1.16e17 || 159 MPa || 81.5 || || 2.93 || 1.47 || || 2.59 || 1835 || 1.01e17 || 148 MPa || 80.7 || || 3.26 || 1.64 || || 2.92 || 1672 || 8.10e16 || 134 MPa || 80.1 || These strengths '''for pure, perfect DWCNT''' are less than 0.2% of the minimum strength needed for a space elevator, and 2% of the strength of [[http://www.torayca.com/en/download/pdf/torayca_t1100g.pdf | Torayca 1100G carbon fiber]]. Furthermore, given these pullout forces (which will be unevenly distributed in real atomically imperfect materials) the '''stretch will not recover'''; these are not spring forces, but disassembly forces. After the material slides apart, it will not go back together, the hysteresis is unity and the creep is unlimited. This is weak taffy, not a strong elastic material like kevlar or carbon fiber, or even a weaker but low creep material like piano wire. || {{ attachment:CNTstrZhang.png | | width=240 }} || In 2004, [[ http://tinyurl.com/Zhang2004 | Zhang, M. et. al. ]] showed this stress/strain curve for CNT yarn in figure 3B. Repeated slow strain cycles slowly pulled the yarns apart, stretching them 11% in 10 cycles (the plunge at the end of the graph is separation failure). A 100,000 km space elevator tether lifting 3600 climbers in a 10 year lifetime can't stretch more than a small fraction of a percent in its lifetime. Plainly, space elevator tethers must be more like piano wire, remaining taut and without enough stretch to "lose tuning" <<BR>><<BR>> [[attachment:CNTstrZhang.png | download separate image ]] || The situation is grim but not completely hopeless. In [[ https://doi.org/10.1557/opl.2015.251 | CNT fibers - yarns between the extremes ]], Dr. Thurid Gspann et. al. suggest that defects create load-sharing crosslinks between tubes, though they reduce tube strength from the theoretical 100 GPa by 30% to 70%. Even with the theoretical "best defect" maximum of 70 GPa, and a density of 1700 kg/m, this '''theoretical''' atomic-precision macro-material will have a strength of 41 Myuri, less than the 48 Myuri (derated by 40% to 34 Myuri) material assumed by the [[ https://www.worldcat.org/oclc/871183396 | 2013 Space Elevators assessment ]]. If 40 Myuri is potentially possible with '''perfect "precision-defect" CNT''' (extrapolated from current knowledge), there ''may be'' an entirely different atomically-perfect 3D material structure with zero hysteresis and '''50 Myuri''' strength. '''''May'' be'''; in 2017, we do not have a scintilla of a clue how to do that. Indeed, these may be pseudo-life-like complex nanostructures that can repair and grow themselves under tension. The details are far beyond our current understanding and technological imagination; enough for a second rate science fiction thriller, but not for practical design. Superlubricity also threatens wheel grip on the space elevator; if substantially all of the CNT fibers are oriented vertically, they will support only nanonewtons of friction force. Our macroscopic experience is that squeezing a fiber increases friction; not so for pure CNT. The 10.5 μm thick tether at the bottom of the reference design space elevator may be a woven net (and fill with ice at the tropopause!), but only the vertical fibers contribute tensile strength, while the horizontal cross ties may create a rough surface but are otherwise dead weight. Much will depend on the tread of the wheels, which will be an engineered surface as difficult to imagine as the tether itself. Space elevators have assumed diamond-like crystal tethers since the 1970s, and carbon nanotube tethers since the 1990s. Neither are strong and stable enough in multitube macroscopic tether form. The materials necessary have not yet been discovered, or even imagined in analyzable detail. ------ == Torayca == [[ https://www.torayca.com/en/lineup/product/pro_001_01.html | data updated 2021/06/25 ]] || || Modulus || Strength || Density || MYuri || wavespeed || || T300-1000 || 230 GPa || 3.53 GPa || 1.76 Mg/m3 || 2.0 || 11.4 km/s || || T1000GB-12000 || 294 GPa || 6.5 GPa || 1.8 Mg/m3 || 3.6 || 12.8 km/s || || T1100GC-12000 || 324 GPa || 7.0 GPa || 1.79 Mg/m3 || 3.9 || 13.5 km/s || |
CNTE
Pure carbon nanotubes exhibit superlubricity - approximately ZERO friction between neighboring tubes in a bundle. In 2013, Zhang et. al. published a paper on carbon nanotube superlubricity that measured the intershell sliding force of a 1 centimeter long double-wall carbon nanotube (DWCNT), pulling a single inner tube out of a centimeter-long outer tube with an atomic force microscope. Three diameters were measured, and the tiny pullout force matched theory, a function of outer tube diameter.
Laurent et. al. estimates that the inner tube diameter is 0.34nm ( d_{s-s} ) less than the outer tube diameter, and that DWCNT density (g/cm³) is:
\rho_{MW} = 6084 g/cm³ { \Large { ( d_{out} ~ - ~ d_{s-s} ) \over { d_{out}^2 } } } with d_{s-s} = 0.34nm and d_{out} in nanometers.
I added my own estimations for perfect hexagonally close packed tube density, tubes/m² = \sqrt( 3 ) / 2 D^2 = 0.866 / D^2 The pullout pressure P = 866 F / D^2 MPa if F is nanonewtons and D is nanometers. Results:
Zhang et. al. |
|
Laurent et. al |
|||||
Diameter |
Pullout |
|
Inner |
Density |
Tubes |
Pullout |
Strength |
nm |
Force nN |
|
nm |
kg/m³ |
/ m² |
Pressure |
Kyuri |
2.73 |
1.37 |
|
2.39 |
1951 |
1.16e17 |
159 MPa |
81.5 |
2.93 |
1.47 |
|
2.59 |
1835 |
1.01e17 |
148 MPa |
80.7 |
3.26 |
1.64 |
|
2.92 |
1672 |
8.10e16 |
134 MPa |
80.1 |
These strengths for pure, perfect DWCNT are less than 0.2% of the minimum strength needed for a space elevator, and 2% of the strength of Torayca 1100G carbon fiber. Furthermore, given these pullout forces (which will be unevenly distributed in real atomically imperfect materials) the stretch will not recover; these are not spring forces, but disassembly forces. After the material slides apart, it will not go back together, the hysteresis is unity and the creep is unlimited. This is weak taffy, not a strong elastic material like kevlar or carbon fiber, or even a weaker but low creep material like piano wire.
|
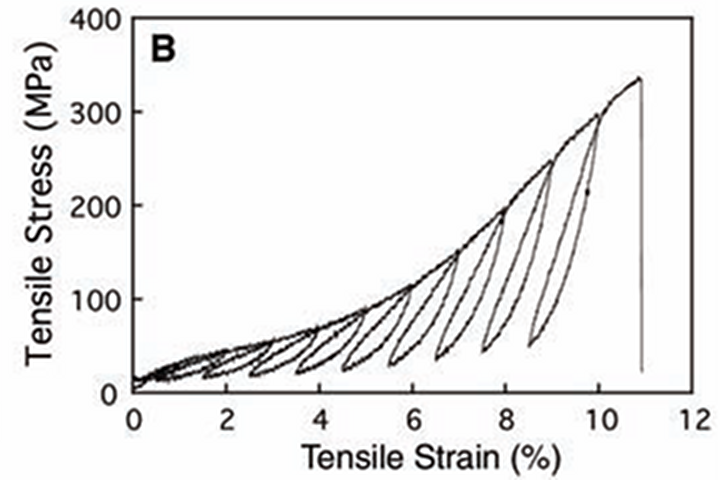
In 2004, Zhang, M. et. al. showed this stress/strain curve for CNT yarn in figure 3B. Repeated slow strain cycles slowly pulled the yarns apart, stretching them 11% in 10 cycles (the plunge at the end of the graph is separation failure). A 100,000 km space elevator tether lifting 3600 climbers in a 10 year lifetime can't stretch more than a small fraction of a percent in its lifetime. Plainly, space elevator tethers must be more like piano wire, remaining taut and without enough stretch to "lose tuning" |
The situation is grim but not completely hopeless. In CNT fibers - yarns between the extremes, Dr. Thurid Gspann et. al. suggest that defects create load-sharing crosslinks between tubes, though they reduce tube strength from the theoretical 100 GPa by 30% to 70%. Even with the theoretical "best defect" maximum of 70 GPa, and a density of 1700 kg/m, this theoretical atomic-precision macro-material will have a strength of 41 Myuri, less than the 48 Myuri (derated by 40% to 34 Myuri) material assumed by the 2013 Space Elevators assessment.
If 40 Myuri is potentially possible with perfect "precision-defect" CNT (extrapolated from current knowledge), there may be an entirely different atomically-perfect 3D material structure with zero hysteresis and 50 Myuri strength. May be; in 2017, we do not have a scintilla of a clue how to do that. Indeed, these may be pseudo-life-like complex nanostructures that can repair and grow themselves under tension. The details are far beyond our current understanding and technological imagination; enough for a second rate science fiction thriller, but not for practical design.
Superlubricity also threatens wheel grip on the space elevator; if substantially all of the CNT fibers are oriented vertically, they will support only nanonewtons of friction force. Our macroscopic experience is that squeezing a fiber increases friction; not so for pure CNT. The 10.5 μm thick tether at the bottom of the reference design space elevator may be a woven net (and fill with ice at the tropopause!), but only the vertical fibers contribute tensile strength, while the horizontal cross ties may create a rough surface but are otherwise dead weight. Much will depend on the tread of the wheels, which will be an engineered surface as difficult to imagine as the tether itself.
Space elevators have assumed diamond-like crystal tethers since the 1970s, and carbon nanotube tethers since the 1990s. Neither are strong and stable enough in multitube macroscopic tether form. The materials necessary have not yet been discovered, or even imagined in analyzable detail.
Torayca
|
Modulus |
Strength |
Density |
MYuri |
wavespeed |
T300-1000 |
230 GPa |
3.53 GPa |
1.76 Mg/m3 |
2.0 |
11.4 km/s |
T1000GB-12000 |
294 GPa |
6.5 GPa |
1.8 Mg/m3 |
3.6 |
12.8 km/s |
T1100GC-12000 |
324 GPa |
7.0 GPa |
1.79 Mg/m3 |
3.9 |
13.5 km/s |