|
Size: 2620
Comment:
|
Size: 3929
Comment: a
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 7: | Line 7: |
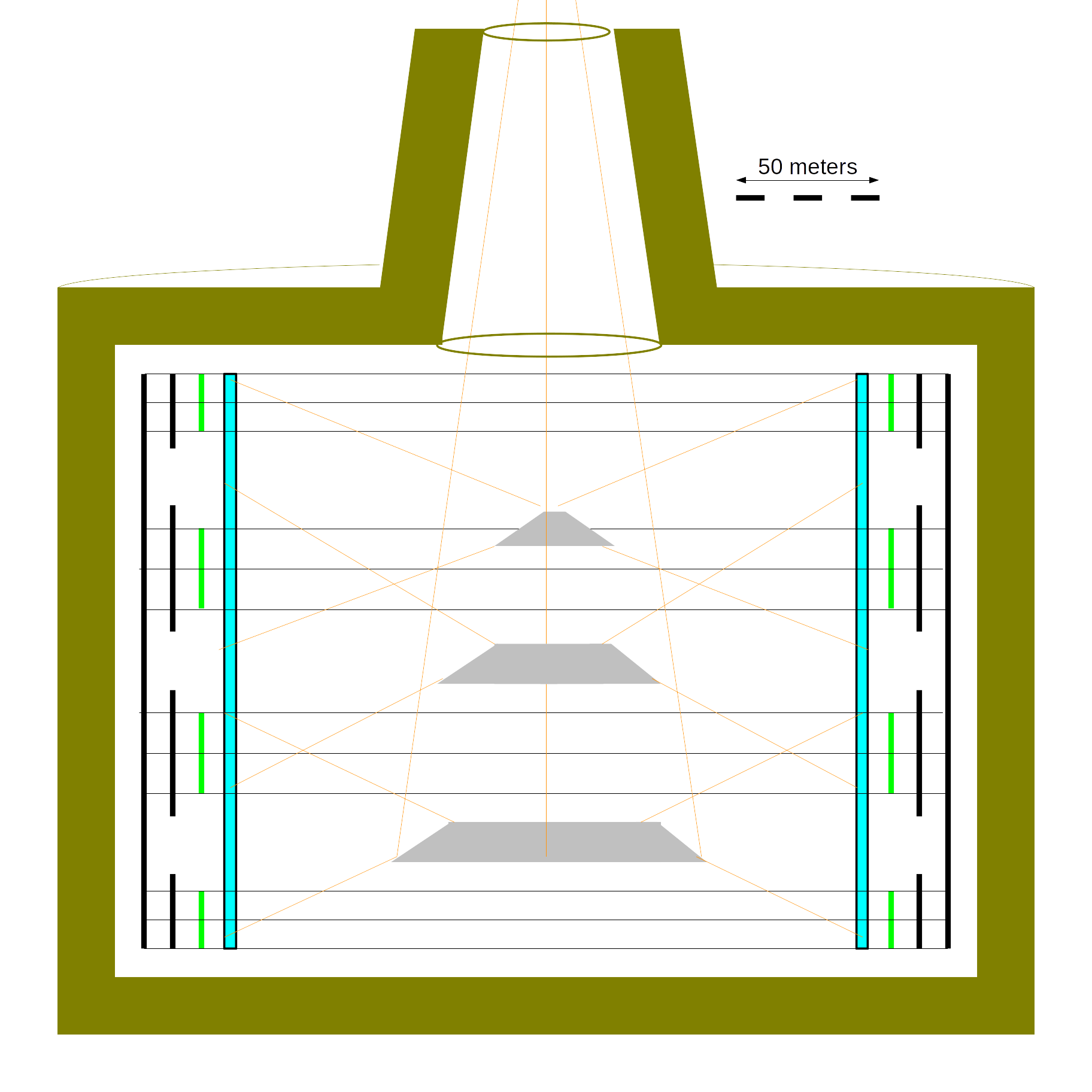
| || {{ attachment:homewheel.png | | width=600 }} || {{ width=200 | | attachment:homewheelmirror.png }} || | || {{ attachment:homewheel.png | | width=600 }} || {{ attachment:homewheelmirror.png | | width=180 }} || As shown, the inner cylinder rotates around its vertical axis, which is perpendicular to the orbital plane. The parabolic mirror focuses sunlight through the narrow hole in the shield; below the focus, the light is diffused by mirrors on the center axis of the habitat to approximate one sun. Hard cosmic radiation will also enter through the hole; the mirrors and the sides of the entry port must be "passivated" so that radiation does not spall and scatter energy into the habitat. The outer shield is a larger cylinder, made from the material of a spinning asteroid, which also supplies the angular momentum to spin the habitat. As shown, it is 20 meters thick. However, as we will see below (and in the attached spreadsheet), the habitat needs a lot more angular momentum than a smallish asteroid can provide, so the asteroid will probably be large enough to provide a vastly thicker shield, in the range of 50 to 100 meters thick, far more than we need for radiation shielding that matches the Earth's magnetic field and atmosphere. Angular momentum, not asteroid mass, may be the limiting factor in asteroid space habitat construction, unless the material is used to make two counter-rotating habitats joined together. In any case, asteroids do not "spin too fast" for this application. |
Large Asteroid Habitat
The habitat geometry is a large cylinder, illuminated by diffusing mirrors on the axis from an external focusing mirror. The habitat is surrounded by a thick shield of dustball asteroid material.
Dustball asteroid rotation rates are quite limited by centrifugal disassembly. For 1200 kg/m³ and a 1.25x safety factor, the rotation period must be longer than 3.37 hours or equatorial material will spin away. The dustball asteroid 101955 Bennu has a rotation period of 4.3 hours, close to the limit, and most asteroids rotate more slowly. Asteroids do not spin too fast; if you hope to spin up a habitat with the angular momentum in the shielding mass, they spin too slowly.
|
|
As shown, the inner cylinder rotates around its vertical axis, which is perpendicular to the orbital plane. The parabolic mirror focuses sunlight through the narrow hole in the shield; below the focus, the light is diffused by mirrors on the center axis of the habitat to approximate one sun. Hard cosmic radiation will also enter through the hole; the mirrors and the sides of the entry port must be "passivated" so that radiation does not spall and scatter energy into the habitat.
The outer shield is a larger cylinder, made from the material of a spinning asteroid, which also supplies the angular momentum to spin the habitat. As shown, it is 20 meters thick. However, as we will see below (and in the attached spreadsheet), the habitat needs a lot more angular momentum than a smallish asteroid can provide, so the asteroid will probably be large enough to provide a vastly thicker shield, in the range of 50 to 100 meters thick, far more than we need for radiation shielding that matches the Earth's magnetic field and atmosphere.
Angular momentum, not asteroid mass, may be the limiting factor in asteroid space habitat construction, unless the material is used to make two counter-rotating habitats joined together. In any case, asteroids do not "spin too fast" for this application.
Bad example, not enough asteroid angular momentum
- Habitat wheel, 1000 kg/m², W = 200 meters wide, R = 140 meters radius. Mass = 2 π R W dens = 1.8e8 kg
- Assume 1 gee, 9.8 m/s² = ω² R = ( 2 π freq )² R, so ω = √0.07 = 0.26458 rad/s, so freq = 0.042 Hz = 2.53 rpm
- Habitat Edge velocity V = ω R = 37 m/s
- Angular momentum L = V R M = 9.1e11 kg m²/s
- Assume Shield thickness 20 m thick, density 1200 kg/m³
- 150 meter inner radius, 170 meter outer radius, 220 meter inner width, 260 meter outer width
Shield Volume = πR₁²W₁ - πR₀²W₀ = π ( 1702*260 - 1502*220 ) m³ = 2360000 m³, Mass ≈ 9.7e9 kg
- Volume of round asteroid = 1986000 m³ = 4 π R³ / 3 so R ≈ 124 meters
- Surface gravity of round asteroid = G M / R² = 6.67408e-11 m³/ kg s² × 9.7e9 kg / 124² m² = 4.2e-5 m/s²
- Assume maximum centrifugal acceleration 0.8 × gravity
thus ω < √( 0.8 × 4/3 × G × ρ ) = 5.18E-4 rad/s → 3.37 hours period
- Maximum asteroid rotation rate ω = √(g/R) = √( 0.8 * 4.2e-5 m/s² / 78 m ) = 5.18e-4 rad/s
- Maximum asteroid angular momentum L = 0.4 M R V = 0.4 × 2e9 × 78² × 5.3e-4 = 3.1e10 kg m²/s
We need a factor of 30 more ... hence the shielding must be at least 8 times heavier and thicker (1.8e10 kg), and the source asteroid larger than 245 meters radius and spinning fast.
Libreoffice Calc ods spreadsheet . . . . (download free, open source libreoffice here )
Near Earth asteroid 101955 Bennu has a mass of 7.3e10 kg, a mean density of 1200 kg/m³, a mean radius of 245 m, and a rotation period of 15500 seconds. L = 0.4 M R² ω = 7e11 kg m²/s, not quite enough!