|
Size: 1353
Comment:
|
Size: 2620
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| ----- The habitat geometry is a large cylinder, illuminated by diffusing mirrors on the axis from an external focusing mirror. The habitat is surrounded by a thick shield of dustball asteroid material. |
|
| Line 3: | Line 5: |
| . Habitat wheel, 2000 kg/m², W = 200 meters wide, R = 140 meters radius. Mass = 2 π R W dens = 3.5e8 kg . Assume 1 gee, 9.8 m/s² = ω² R = ( 2 π freq )² R, so ω = √0.07 = 0.26458 rad/s, so freq = 0.042 Hz = 2.52 rpm . Edge velocity V = ω R = 37 m/s . Angular momentum L = V R M = 1.81e12 kg m²/s |
Dustball asteroid rotation rates are quite limited by centrifugal disassembly. For 1200 kg/m³ and a 1.25x safety factor, the rotation period must be longer than 3.37 hours or equatorial material will spin away. The dustball asteroid 101955 Bennu has a rotation period of 4.3 hours, close to the limit, and most asteroids rotate more slowly. Asteroids do not spin too fast; if you hope to spin up a habitat with the angular momentum in the shielding mass, they spin too slowly. |
| Line 8: | Line 7: |
| . Shield 20 m thick, density 1000 kg/m³ 150 meter inner radius, 170 meter outer radius, 220 meter inner width, 240 meter outer width. . Shield Volume = πR₁²W₁ - πR₀²W₀ = π ( 170^2*240 - 150^2*220 ) m³ = 1986000 m³, Mass ≈ 2e9 kg . Volume of round asteroid = 1986000 m³ = 4 π R³ / 3 so R ≈ 78 meters . Surface gravity of round asteroid = G M / R² = 6.67408e-11 m³/ kg s² × 2e9 kg / 78² m² = 2.2e-5 m/s² . Maximum asteroid rotation rate ω = √ g/R = √ ( 2.2e-5 m/s² / 78 m ) = 5.3e-4 rad/s 3.3 . Maximum asteroid angular momentum L = 0.4 M R² ω = 0.4 × 2e9 × 78² × 5.3e-4 = 2e11 kg m²/s |
|| {{ attachment:homewheel.png | | width=600 }} || {{ attachment:homewheelmirror.png | | width=180 }} || |
| Line 15: | Line 9: |
| We need a factor of 9 more ... hence the shielding must be at least 9 times heavier and thicker (1.8e10 kg), and the source asteroid larger than 160 meters diameter. | == Bad example, not enough asteroid angular momentum == |
| Line 17: | Line 11: |
| Near Earth asteroid 101955 Bennu has a mass of 7.3e10 kg, a mean density of 1200 kg/m³, a mean radius of 245 m, and a rotation period of 15500 seconds. L = 0.4 M R² ω = 7e11 kg m²/s | . Habitat wheel, 1000 kg/m², W = 200 meters wide, R = 140 meters radius. Mass = 2 π R W dens = 1.8e8 kg . Assume 1 gee, 9.8 m/s² = ω² R = ( 2 π freq )² R, so ω = √0.07 = 0.26458 rad/s, so freq = 0.042 Hz = 2.53 rpm . Habitat Edge velocity V = ω R = 37 m/s . Angular momentum L = V R M = 9.1e11 kg m²/s . Assume Shield thickness 20 m thick, density 1200 kg/m³ . 150 meter inner radius, 170 meter outer radius, 220 meter inner width, 260 meter outer width . Shield Volume = πR₁²W₁ - πR₀²W₀ = π ( 170^2*260 - 150^2*220 ) m³ = 2360000 m³, Mass ≈ 9.7e9 kg . Volume of round asteroid = 1986000 m³ = 4 π R³ / 3 so R ≈ 124 meters . Surface gravity of round asteroid = G M / R² = 6.67408e-11 m³/ kg s² × 9.7e9 kg / 124² m² = 4.2e-5 m/s² . Assume maximum centrifugal acceleration 0.8 × gravity . thus ω < √( 0.8 × 4/3 × G × ρ ) = 5.18E-4 rad/s → 3.37 hours period . Maximum asteroid rotation rate ω = √(g/R) = √( 0.8 * 4.2e-5 m/s² / 78 m ) = 5.18e-4 rad/s . Maximum asteroid angular momentum L = 0.4 M R V = 0.4 × 2e9 × 78² × 5.3e-4 = 3.1e10 kg m²/s We need a factor of 30 more ... hence the shielding must be at least 8 times heavier and thicker (1.8e10 kg), and the source asteroid larger than 245 meters radius and spinning fast. [[ attachment:astrohabitat.ods | Libreoffice Calc ods spreadsheet ]] . . . . (download free, open source libreoffice [[ https://www.libreoffice.org/download/download/ | here ]] ) Near Earth asteroid 101955 Bennu has a mass of 7.3e10 kg, a mean density of 1200 kg/m³, a mean radius of 245 m, and a rotation period of 15500 seconds. L = 0.4 M R² ω = 7e11 kg m²/s, not quite enough! MoreLater |
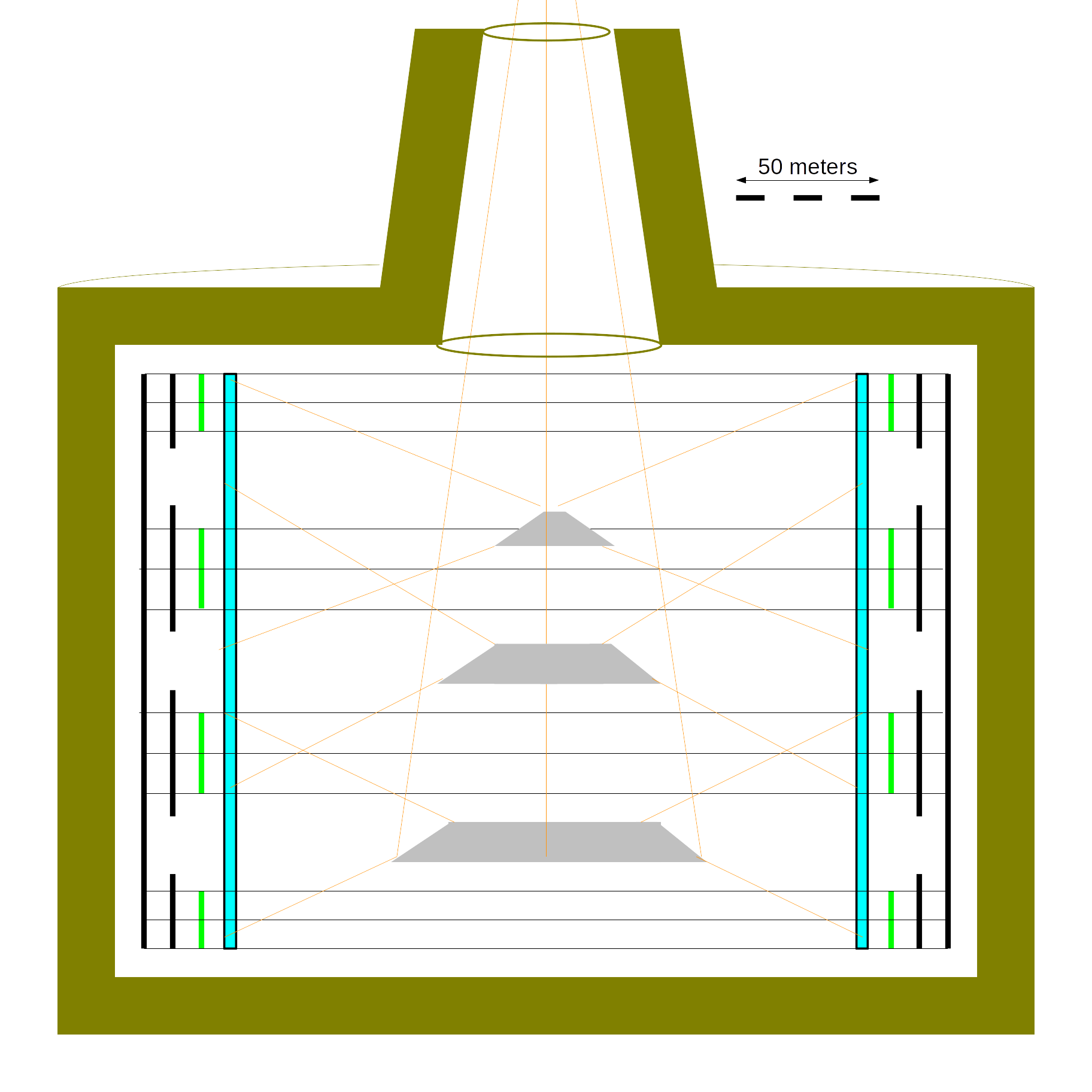
Large Asteroid Habitat
The habitat geometry is a large cylinder, illuminated by diffusing mirrors on the axis from an external focusing mirror. The habitat is surrounded by a thick shield of dustball asteroid material.
Dustball asteroid rotation rates are quite limited by centrifugal disassembly. For 1200 kg/m³ and a 1.25x safety factor, the rotation period must be longer than 3.37 hours or equatorial material will spin away. The dustball asteroid 101955 Bennu has a rotation period of 4.3 hours, close to the limit, and most asteroids rotate more slowly. Asteroids do not spin too fast; if you hope to spin up a habitat with the angular momentum in the shielding mass, they spin too slowly.
|
|
Bad example, not enough asteroid angular momentum
- Habitat wheel, 1000 kg/m², W = 200 meters wide, R = 140 meters radius. Mass = 2 π R W dens = 1.8e8 kg
- Assume 1 gee, 9.8 m/s² = ω² R = ( 2 π freq )² R, so ω = √0.07 = 0.26458 rad/s, so freq = 0.042 Hz = 2.53 rpm
- Habitat Edge velocity V = ω R = 37 m/s
- Angular momentum L = V R M = 9.1e11 kg m²/s
- Assume Shield thickness 20 m thick, density 1200 kg/m³
- 150 meter inner radius, 170 meter outer radius, 220 meter inner width, 260 meter outer width
Shield Volume = πR₁²W₁ - πR₀²W₀ = π ( 1702*260 - 1502*220 ) m³ = 2360000 m³, Mass ≈ 9.7e9 kg
- Volume of round asteroid = 1986000 m³ = 4 π R³ / 3 so R ≈ 124 meters
- Surface gravity of round asteroid = G M / R² = 6.67408e-11 m³/ kg s² × 9.7e9 kg / 124² m² = 4.2e-5 m/s²
- Assume maximum centrifugal acceleration 0.8 × gravity
thus ω < √( 0.8 × 4/3 × G × ρ ) = 5.18E-4 rad/s → 3.37 hours period
- Maximum asteroid rotation rate ω = √(g/R) = √( 0.8 * 4.2e-5 m/s² / 78 m ) = 5.18e-4 rad/s
- Maximum asteroid angular momentum L = 0.4 M R V = 0.4 × 2e9 × 78² × 5.3e-4 = 3.1e10 kg m²/s
We need a factor of 30 more ... hence the shielding must be at least 8 times heavier and thicker (1.8e10 kg), and the source asteroid larger than 245 meters radius and spinning fast.
Libreoffice Calc ods spreadsheet . . . . (download free, open source libreoffice here )
Near Earth asteroid 101955 Bennu has a mass of 7.3e10 kg, a mean density of 1200 kg/m³, a mean radius of 245 m, and a rotation period of 15500 seconds. L = 0.4 M R² ω = 7e11 kg m²/s, not quite enough!