|
Size: 4115
Comment:
|
Size: 6788
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 4: | Line 4: |
| THe current reference space elevator design assumes solar-powered climbers. This assumes that vast areas of solar panels can cantilever from the sides of a climber - in gravity - and provide megawatts of climb power, while being lightweight and affordable. The example pictured is a DLR solar sail, intended for microgravity, NOT an array of solar cells. Solar sails are ultrathin plastic films covered with just enough shiny metal to reflect light. Aluminum conductivity is 2.8e-8 ohm/meter; a film with 10 ohm per square resistivity (95% reflective) is 2.8e-9 meters thick - a few atomic layers. The density is 2700 kg per cubic meter, works out to 8 kilograms per square kilometer on top of the plastic. This is far less than actual satellite solar panels (300 W/m^2^, 1 kg/m^2^), which are designed for microgravity, not to deploy in a gravity field. These arrays are stabilized by gravitational gradients in orbit, and they are test-deployed on the ground hanging sideways from heavy structure. | The current reference space elevator design assumes solar-powered climbers. This assumes that vast areas of solar panels can cantilever from the sides of a climber - in gravity - and provide megawatts of climb power, while being lightweight and affordable. .'''Solar cell self powered climbers are unlikely:''' The example pictured is a DLR solar sail (passive light pressure nanothrust), intended for microgravity, NOT an array of solar cells. Solar sails are ultrathin plastic films covered with just enough shiny metal to reflect light. Aluminum conductivity is 2.8e-8 ohm/meter; a film with 10 ohm per square resistivity (95% reflective) is 2.8e-9 meters thick - a few atomic layers. The density is 2700 kg per cubic meter, works out to 8 kilograms per square kilometer on top of the plastic. This is far less than actual satellite solar panels (300 W/m^2^, 1 kg/m^2^), which are designed for microgravity, not to deploy in a gravity field. Actual space solar arrays are stabilized by gravitational gradients in orbit, and they are test-deployed on the ground hanging sideways from heavy structure. |
| Line 10: | Line 12: |
| ~+That's the old stuff. This is morphing into a pair of low inertia electrical motors separated by a quarter wave, with electrical power conversion at each motor, with power cable and stiff tether between. | ~+That paper is old, a new one will be written with the material here. This is morphing into two banks of electrical motors separated by a quarter wave, with electrical power conversion at each motor group, and a power cable and stiff tether in between them.+~ |
| Line 12: | Line 14: |
| ----- Click image for larger view or download [[attachment:ClimberPickoff.png | {{ attachment:ClimberPickoff.png | | height=400 }} ]] [[ attachment:ClimberPickoff.odg | !LibreOffice source ]] A cheesy drawing of the two motor group "wheels". The grey "foot" makes contact to the tether when it passes by at maximum velocity. Alternating wheels have feet that turn in opposite directions, and the red and blue "free wheels" help maintain spacing but do not provide power. The power wheels turn at half the power vibration rate. |
|
| Line 19: | Line 27: |
---- == Electrical cable == ==== Relationship between voltage and current in a uniform lossless electronic signal cable: ==== $ ~~~~~~~~ { \Large {{ \partial V(x,t) } \over { \partial x }} } = - L { \Large { {\partial I(x,t) } \over { \partial t }} } ~~~~~~~~~~~ { \Large {{ \partial I(x,t) } \over { \partial x }} } = - C { \Large {{ \partial V(x,t) } \over { \partial t }} } $ |
|
| Line 41: | Line 58: |
| MoreLater | ---- == Mechanical cable == . $ \Psi(x,t) $ displacement from rest of a cable element in meters at a specific distance $ x $ and time $ t $ . $ v(x,t) $ displacement velocity a cable element in meters at a specific distance $ x $ and time $ t $ . $ a(x,t) $ displacement acceleration a cable element in meters at a specific distance $ x $ and time $ t $ . $ e(x,t) $ strain of a cable element in meters at a specific distance $ x $ and time $ t $ . $ f(x,t) $ force on a cable element in meters at a specific distance $ x $ and time $ t $ . $ x $ = distance along cable in meters . $ t $ = time in seconds . $ Y_c $ cable spring constant, Newtons, Young's modulus $ Y $ times cross section $ A $ . $ \rho_c = \rho A $ cable density, kilograms per meter, density $ \rho $ times cross section $ A $ ==== Relationship between displacement, velocity, acceleration, tension, and strain in a mechanical cable: ==== $ ~~~~~~~~ { \large e(x,t) = \Large {{ \partial \psi(x,t) } \over { \partial x }} } $ $ ~~~~~~~~ { \large f(x,t) = Y_c \Large { { \partial e(x,t) } \over { \partial x }} }~=~{ Y_c \Large {{ \partial^2 \psi(x,t) } \over { \partial x^2 }} } $ $ ~~~~~~~~ { \large v(x,t) = \Large {{ \partial \psi(x,t) } \over { \partial t }} } $ $ ~~~~~~~~ { \large a(x,t) = \Large {{ \partial^2 \psi(x,t) } \over { \partial t^2 }} }~=~{\LARGE{ 1 \over \rho_c }}~{\large f(x,t)} ~=~ { \Large { Y_c \over \rho_c } ~ {{ \partial^2 \psi(x,t) } \over { \partial x^2 }} } $ |
| Line 45: | Line 84: |
| . $ \Psi(x,t) $ displacement from rest of a cable element in meters at a specific distance $ x $ and time $ t $ . $ x $ = distance along cable in meters . $ t $ = time in seconds . $ Y_c $ cable spring constant, Newtons, Young's modulus times cross section . $ \rho_c $ cable density, kilograms per meter, density times cross section $~~~ \rho_c { \Large {{ \partial^2 \Psi(x,t) } \over { \partial t^2 }} } ~=~ Y_c { \Large {{ \partial^2 \Psi(x,t) } \over { \partial x^2 }} } $ |
displacement: $~~{\Large{{\partial^2 \Psi(x,t)}\over{\partial t^2}} } = {\Large{Y_c \over \rho_c }~{{\partial^2 \Psi(x,t)}\over{\partial x^2 }} }~~~~$ velocity: $~~{\Large{{\partial^2 v(x,t)}\over{\partial t^2}} } = {\Large{Y_c \over \rho_c}~{{\partial^2 v(x,t)}\over{ \partial x^2}} }~~~~$ strain: $~~{\Large{{\partial^2 e(x,t)}\over{\partial t^2}} } = {\Large{Y_c \over \rho_c}~{{\partial^2 e(x,t)}\over{\partial x^2}} }$ For sinusoidal waves, $ ~~~~~~~~ v(x,t) = v_0 \sin( \omega t + k x ) ~~~~~ $ and $ ~~~~~ e(x,t) = e_0 \sin( \omega t + k x ) $ MoreLater, check the sign on $ e $ |
| Line 54: | Line 93: |
| MoreLater |
Acoustic Climber for Space Elevator
The current reference space elevator design assumes solar-powered climbers. This assumes that vast areas of solar panels can cantilever from the sides of a climber - in gravity - and provide megawatts of climb power, while being lightweight and affordable.
Solar cell self powered climbers are unlikely: The example pictured is a DLR solar sail (passive light pressure nanothrust), intended for microgravity, NOT an array of solar cells. Solar sails are ultrathin plastic films covered with just enough shiny metal to reflect light. Aluminum conductivity is 2.8e-8 ohm/meter; a film with 10 ohm per square resistivity (95% reflective) is 2.8e-9 meters thick - a few atomic layers. The density is 2700 kg per cubic meter, works out to 8 kilograms per square kilometer on top of the plastic. This is far less than actual satellite solar panels (300 W/m2, 1 kg/m2), which are designed for microgravity, not to deploy in a gravity field. Actual space solar arrays are stabilized by gravitational gradients in orbit, and they are test-deployed on the ground hanging sideways from heavy structure.
Instead, a superstrong tether can carry megawatts of subkilohertz acoustic power, which can be impedance-matched and mechanically rectified (mad handwaving here) to produce climber thrust. The acoustic transmitters on the ground and at GEO node can provide 2 MW and 10 MW of climb power respectively, more by trading off climber mass, gravitational weight, and climber speed. Climbers will have a mechanical receiver that transforms vibration to rotary wheel motion.
That paper is old, a new one will be written with the material here. This is morphing into two banks of electrical motors separated by a quarter wave, with electrical power conversion at each motor group, and a power cable and stiff tether in between them.
Click image for larger view or download 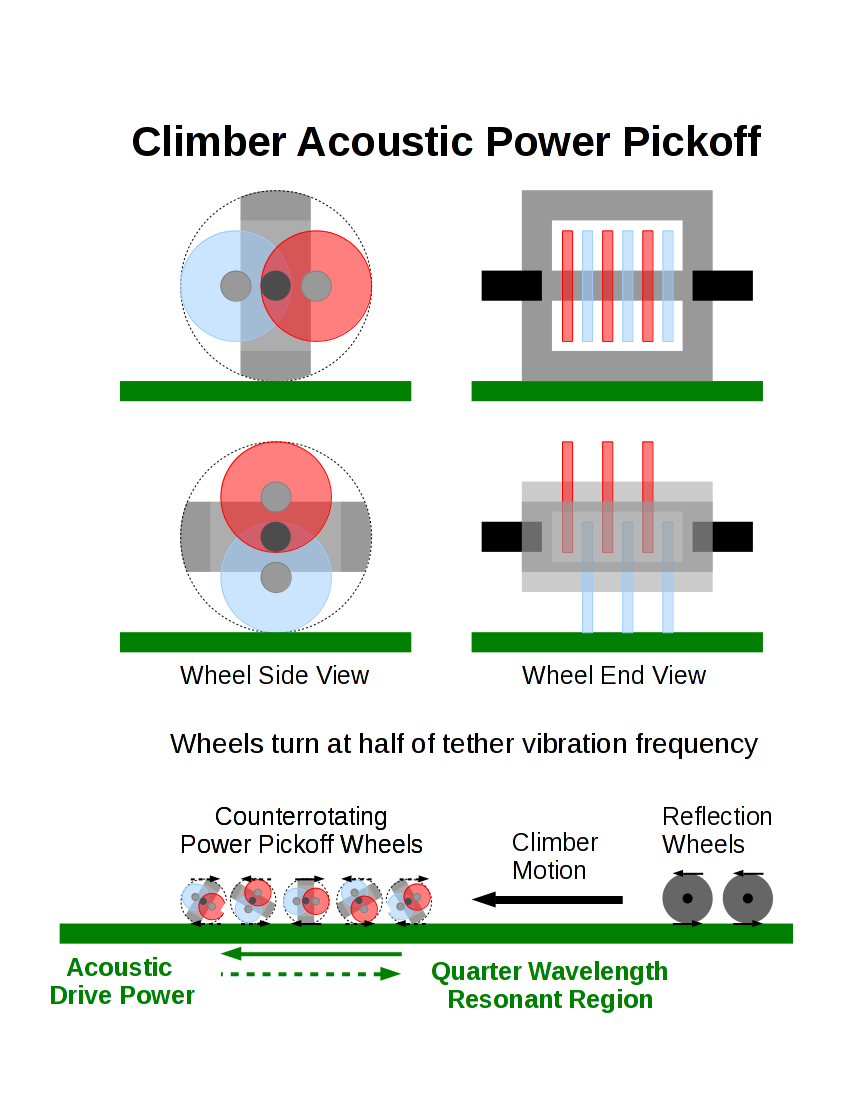 !LibreOffice source
!LibreOffice source
A cheesy drawing of the two motor group "wheels". The grey "foot" makes contact to the tether when it passes by at maximum velocity. Alternating wheels have feet that turn in opposite directions, and the red and blue "free wheels" help maintain spacing but do not provide power. The power wheels turn at half the power vibration rate.
Analogy Between an Electronic Signal Cable and a Stiff Tether
All units MKS: meters, kilograms, seconds, volts, amperes (amps), radians
( FYI: if you don't think radians are a unit, you are turned around, and can't distinguish energy from torque. ![]() )
)
Electrical cable
Relationship between voltage and current in a uniform lossless electronic signal cable:
~~~~~~~~ { \Large {{ \partial V(x,t) } \over { \partial x }} } = - L { \Large { {\partial I(x,t) } \over { \partial t }} } ~~~~~~~~~~~ { \Large {{ \partial I(x,t) } \over { \partial x }} } = - C { \Large {{ \partial V(x,t) } \over { \partial t }} }
Wave equations for a uniform lossless electronic signal cable:
~~~ L C ~ { \Large {{ \partial^2 I(x,t) } \over { \partial t^2 }} } ~=~ { \Large {{ \partial^2 I(x,t) } \over { \partial x^2 }} } ~~~~~ L C ~ { \Large {{ \partial^2 V(x,t) } \over { \partial t^2 }} } ~=~ { \Large {{ \partial^2 V(x,t) } \over { \partial x^2 }}}
I(x,t) = current in amps at a specific distance x and time t
V(x,t) = voltage in volts at a specific distance x and time t
x = distance along cable in meters
t = time in seconds
C = capacitance per unit length, farads per meter
L = inductance per unit length, henrys per meter
Sinusoidal solutions (many others are possible): ~~~I(x,t) = I_0 \sin( \omega t + k x ) amps ~~~~~ V(x,t) = V_0 \sin( \omega t + k x ) volts
frequency ~ \omega ~ ~ radians per second
wavenumber ~ k ~ = ~ \pm \sqrt{ L C } ~ \omega ~ ~ radians per meter
speed ~ v ~ = ~ \omega / k ~ = ~ \pm 1 / \sqrt{ L C } ~ ~ in the +x or -x direction, a large fraction of the speed of light
a function of the materials used, typically around 0.5c or 150 million meters per second
impedance ~ Z ~ = ~ \sqrt{ L / C } ~ = ~ V_0 / I_0 ~ ~ ohms
- a function of the materials used and cross section, typically around 50 ohms but can be higher than 100 ohms and lower than 10 ohms
Mechanical cable
\Psi(x,t) displacement from rest of a cable element in meters at a specific distance x and time t
v(x,t) displacement velocity a cable element in meters at a specific distance x and time t
a(x,t) displacement acceleration a cable element in meters at a specific distance x and time t
e(x,t) strain of a cable element in meters at a specific distance x and time t
f(x,t) force on a cable element in meters at a specific distance x and time t
x = distance along cable in meters
t = time in seconds
Y_c cable spring constant, Newtons, Young's modulus Y times cross section A
\rho_c = \rho A cable density, kilograms per meter, density \rho times cross section A
Relationship between displacement, velocity, acceleration, tension, and strain in a mechanical cable:
~~~~~~~~ { \large e(x,t) = \Large {{ \partial \psi(x,t) } \over { \partial x }} }
~~~~~~~~ { \large f(x,t) = Y_c \Large { { \partial e(x,t) } \over { \partial x }} }~=~{ Y_c \Large {{ \partial^2 \psi(x,t) } \over { \partial x^2 }} }
~~~~~~~~ { \large v(x,t) = \Large {{ \partial \psi(x,t) } \over { \partial t }} }
~~~~~~~~ { \large a(x,t) = \Large {{ \partial^2 \psi(x,t) } \over { \partial t^2 }} }~=~{\LARGE{ 1 \over \rho_c }}~{\large f(x,t)} ~=~ { \Large { Y_c \over \rho_c } ~ {{ \partial^2 \psi(x,t) } \over { \partial x^2 }} }
Wave equations for a uniform lossless mechanical cable:
displacement: ~~{\Large{{\partial^2 \Psi(x,t)}\over{\partial t^2}} } = {\Large{Y_c \over \rho_c }~{{\partial^2 \Psi(x,t)}\over{\partial x^2 }} }~~~~ velocity: ~~{\Large{{\partial^2 v(x,t)}\over{\partial t^2}} } = {\Large{Y_c \over \rho_c}~{{\partial^2 v(x,t)}\over{ \partial x^2}} }~~~~ strain: ~~{\Large{{\partial^2 e(x,t)}\over{\partial t^2}} } = {\Large{Y_c \over \rho_c}~{{\partial^2 e(x,t)}\over{\partial x^2}} }
For sinusoidal waves,
~~~~~~~~ v(x,t) = v_0 \sin( \omega t + k x ) ~~~~~ and ~~~~~ e(x,t) = e_0 \sin( \omega t + k x )
MoreLater, check the sign on e
